Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

Integral od x^x *(1+lnx)dx
WWW:

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
filipnet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: muško
Sarma = la pohva - posuda
24 = 29 - 5
Lokacija: cvrsto na stolici
PostPostano: 23:41 pon, 23. 8. 2004    Naslov: Integral od x^x *(1+lnx)dx Citirajte i odgovorite
trebam pomoc! Kak da integriram
x^x *(1+lnx)dx
Neznam kaj da radim s ovim x^x?
:roll:
Hvala unaprijed!
trebam pomoc! Kak da integriram
x^x *(1+lnx)dx
Neznam kaj da radim s ovim x^x?
Rolling Eyes
Hvala unaprijed!



_________________
Dwarf Everything happens with a reason! Vidi me kako skaaaaaceeeem!
[Vrh]
Korisnički profil Pošaljite privatnu poruku
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 23:48 pon, 23. 8. 2004    Naslov: Citirajte i odgovorite
x^x =: y / ln
x ln x = ln y / D
ln x + x/x = y'/y
y' = y * (ln x + 1)
y' = x^x * (ln x + 1)

Pa, kad to integriras, dobijes x^x (osim ako sam negdje opako promasio). 8)
x^x =: y / ln
x ln x = ln y / D
ln x + x/x = y'/y
y' = y * (ln x + 1)
y' = x^x * (ln x + 1)

Pa, kad to integriras, dobijes x^x (osim ako sam negdje opako promasio). Cool



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
anamarija
Gost
PostPostano: 17:30 pon, 30. 8. 2004    Naslov: Citirajte i odgovorite
Ako ne grijesim, to je Frankin zadatak s roka u drugom mjesecu....
Moje rjesenje tog zadatka bilo bi:
s obzirom da je pod integralom x^x*(1+lnx), ovo x^x zapisem kao e^xlnx. Sad pod integralom imam to i jos *(1+lnx). Zar deriviranjem izraza e^xlnx ne dobijem upravo to sto imam pod integralom? Po meni bi rjesenje bilo upravo to! No, u zadatku su dane granice: integral ide od 0 do 2. Kad u e^xlnx uvrstim 0 i 2, dobijem e^2ln2 -e^0ln0. S obzirom da ln0 nije definiran, rjesenje je e^2ln2.
Jesam li u pravu ili u zabludi?!
Ako ne grijesim, to je Frankin zadatak s roka u drugom mjesecu....
Moje rjesenje tog zadatka bilo bi:
s obzirom da je pod integralom x^x*(1+lnx), ovo x^x zapisem kao e^xlnx. Sad pod integralom imam to i jos *(1+lnx). Zar deriviranjem izraza e^xlnx ne dobijem upravo to sto imam pod integralom? Po meni bi rjesenje bilo upravo to! No, u zadatku su dane granice: integral ide od 0 do 2. Kad u e^xlnx uvrstim 0 i 2, dobijem e^2ln2 -e^0ln0. S obzirom da ln0 nije definiran, rjesenje je e^2ln2.
Jesam li u pravu ili u zabludi?!


[Vrh]
anamarija
Gost
PostPostano: 17:36 pon, 30. 8. 2004    Naslov: Citirajte i odgovorite
To je zapravo ono sto je vsego dobio, naravno s granicama, ali me zanima da li je rj tocno zbog postupka i ln0. :D
To je zapravo ono sto je vsego dobio, naravno s granicama, ali me zanima da li je rj tocno zbog postupka i ln0. Very Happy


[Vrh]
mdoko
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: muško
Sarma = la pohva - posuda
199 = 237 - 38
Lokacija: Heriot-Watt University, Edinburgh
PostPostano: 18:34 pon, 30. 8. 2004    Naslov: Citirajte i odgovorite
Kako [latex]0^0[/latex] nije definirano (da ne ulazimo u slozenije rasprave) radi se o nepravom integralu. Dakle:
[latex] \int_{0}^{2}x^xdx = \lim_{a \to 0} \int_{a}^{2}x^xdx = \lim_{a \to 0}(2^2 - a^a) = 4 - 1 = 3[/latex]

Gornji limes se rjesava na sljedeci nacin:

[latex] \lim_{x \to 0}x^x = \lim_{x \to 0}e^{x\ln x} = e^{\lim_{x \to 0}x\ln x}[/latex]

Rjesimo:
[latex]\lim_{x \to 0}x\ln x= \lim_{x \to 0}\frac{\ln x}{x^{-1}} = [/latex] po L'Hospitalu [latex]= \lim_{x \to 0}\frac{x^{-1}}{-x^{-2}} = \lim_{x \to 0}(-x) = 0[/latex]
Dakle:
[latex]\lim_{x \to 0}x^x = e^0 = 1[/latex]
Kako nije definirano (da ne ulazimo u slozenije rasprave) radi se o nepravom integralu. Dakle:


Gornji limes se rjesava na sljedeci nacin:



Rjesimo:
po L'Hospitalu
Dakle:



_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
[Vrh]
Korisnički profil Pošaljite privatnu poruku Posjetite Web stranice
fmb
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 02. 2004. (12:34:47)
Postovi: (B6)16
Sarma = la pohva - posuda
12 = 16 - 4
PostPostano: 11:18 sri, 1. 9. 2004    Naslov: Citirajte i odgovorite
[quote="anamarija"]Ako ne grijesim, to je Frankin zadatak s roka u drugom mjesecu....
Moje rjesenje tog zadatka bilo bi:
s obzirom da je pod integralom x^x*(1+lnx), ovo x^x zapisem kao e^xlnx. Sad pod integralom imam to i jos *(1+lnx). Zar deriviranjem izraza e^xlnx ne dobijem upravo to sto imam pod integralom? Po meni bi rjesenje bilo upravo to! No, u zadatku su dane granice: integral ide od 0 do 2. Kad u e^xlnx uvrstim 0 i 2, dobijem e^2ln2 -e^0ln0. S obzirom da ln0 nije definiran, rjesenje je e^2ln2.
Jesam li u pravu ili u zabludi?![/quote]

Da, to je moj zadatak. I pod "Greske na MA1 i MA2" sam detaljno objasnila sve sto je tu "problematicno". Iako mislim da nije nis problematicno jer bi student matematike na kraju prve godine trebao ipak znati definiciju opce potencije kao i da ako nesto nije definirano, to ne zanci da je to jednako nuli...

FMB :patkica:
anamarija (napisa):
Ako ne grijesim, to je Frankin zadatak s roka u drugom mjesecu....
Moje rjesenje tog zadatka bilo bi:
s obzirom da je pod integralom x^x*(1+lnx), ovo x^x zapisem kao e^xlnx. Sad pod integralom imam to i jos *(1+lnx). Zar deriviranjem izraza e^xlnx ne dobijem upravo to sto imam pod integralom? Po meni bi rjesenje bilo upravo to! No, u zadatku su dane granice: integral ide od 0 do 2. Kad u e^xlnx uvrstim 0 i 2, dobijem e^2ln2 -e^0ln0. S obzirom da ln0 nije definiran, rjesenje je e^2ln2.
Jesam li u pravu ili u zabludi?!


Da, to je moj zadatak. I pod "Greske na MA1 i MA2" sam detaljno objasnila sve sto je tu "problematicno". Iako mislim da nije nis problematicno jer bi student matematike na kraju prve godine trebao ipak znati definiciju opce potencije kao i da ako nesto nije definirano, to ne zanci da je to jednako nuli...

FMB Patkica



_________________
"Have patience. Go where you must, and hope."
(Gandalf in J.R.R.Tolkien's "The Lord of the Rings")
[Vrh]
Korisnički profil Pošaljite privatnu poruku Posjetite Web stranice
SvekY
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 21. 11. 2003. (23:44:22)
Postovi: (FF)16
Spol: muško
Sarma = la pohva - posuda
11 = 14 - 3
Lokacija: unitarni vektorski prostor
PostPostano: 22:02 uto, 14. 9. 2004    Naslov: novi integral Citirajte i odgovorite
Imam integral koji ne znam rjesiti, a mislim da spada pod ovu temu.

Integral glasi [b]1/ ( x * (13- 4 ln(x) + ln(x)^2)^2 )[/b] po x.

Prvo zamjena [i]t=ln(x)[/i], onda sam u nazivniku sveo na potpun kvadrat:
[i]13 - 4t + t^2 = (t-2)^2 +9[/i]
pa opet zamjena [i]t-2=u[/i].

Dobio sam integral od [b]1/ ( (u^2+9)^2 )[/b] po u.

Kako dalje? :?:
Imam integral koji ne znam rjesiti, a mislim da spada pod ovu temu.

Integral glasi 1/ ( x * (13- 4 ln(x) + ln(x)^2)^2 ) po x.

Prvo zamjena t=ln(x), onda sam u nazivniku sveo na potpun kvadrat:
13 - 4t + t^2 = (t-2)^2 +9
pa opet zamjena t-2=u.

Dobio sam integral od 1/ ( (u^2+9)^2 ) po u.

Kako dalje? Question


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Sarma = la pohva - posuda
7 = 12 - 5
Lokacija: hm?
PostPostano: 22:36 uto, 14. 9. 2004    Naslov: Re: novi integral Citirajte i odgovorite
[quote="SvekY"]Dobio sam integral od [b]1/ ( (u^2+9)^2 )[/b] po u.

Kako dalje? :?:[/quote]
:-k mislis...
[latex]\displaystyle \int \frac{du}{(u^2+9)^2}[/latex]
:? ?
SvekY (napisa):
Dobio sam integral od 1/ ( (u^2+9)^2 ) po u.

Kako dalje? Question

Think mislis...

Confused ?



_________________

Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk Wink
[Vrh]
Korisnički profil Pošaljite privatnu poruku Posjetite Web stranice
Vincent Van Ear
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
Sarma = la pohva - posuda
-1 = 1 - 2
PostPostano: 23:31 uto, 14. 9. 2004    Naslov: Re: novi integral Citirajte i odgovorite
[quote="ZELENIZUBNAPLANETIDOSADE"][quote="SvekY"]Dobio sam integral od [b]1/ ( (u^2+9)^2 )[/b] po u.

Kako dalje? :?:[/quote]
:-k mislis...
[latex]\displaystyle \int \frac{du}{(u^2+9)^2}[/latex]
:? ?[/quote]

Ja bi to probao ovako:

[color=green]S du/(u^2+9)^2 =

= 1/9 * S ( (u^2 + 9) – u^2 / (u^2 + 9)^2 )du =

=1/9 * S ( (u^2 + 9) / (u^2 + 9)^2 )du - 1/9 * S ( u^2 / (u^2 + 9)^2 )du =[/color]

mislim da češ dalje znati,prvi integral ti je tablični baš kao i drugi,ako drugoga nemaš u tablici onda ga napadni metodom parcijalne integracije s time da ti je funkcija za deriviranje u,a ona za integriranje u/(u^2+9)^2 što neće biti problem integrirati jer metoda supstitucije obavlja posao na trivijalan način.
:wink:

BTW,Sveky,jedna preporuka-imaš zbirku od Apsena number 2 gdje ti autor postupno rješava svakakve oblike integrala,zbirka je i više no pedagoška jer ti proda postupak rješavanja pojedinog integrala i onda nakon usvajanja finte rješavaš dalje,svaki put kada se pojavi integral sa novom fintom autor ti to lijepo objelodani tak da nemaš nikakvog beda.
Nakon što polomiš Apsena slijedi finalni meč :D sa legendarnim rusom Demidovičem.
Nakon takva drilanja spreman si se suočiti sa svakim integralom,uživaj.
ZELENIZUBNAPLANETIDOSADE (napisa):
SvekY (napisa):
Dobio sam integral od 1/ ( (u^2+9)^2 ) po u.

Kako dalje? Question

Think mislis...

Confused ?


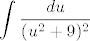
Ja bi to probao ovako:

S du/(u^2+9)^2 =

= 1/9 * S ( (u^2 + 9) – u^2 / (u^2 + 9)^2 )du =

=1/9 * S ( (u^2 + 9) / (u^2 + 9)^2 )du - 1/9 * S ( u^2 / (u^2 + 9)^2 )du =

mislim da češ dalje znati,prvi integral ti je tablični baš kao i drugi,ako drugoga nemaš u tablici onda ga napadni metodom parcijalne integracije s time da ti je funkcija za deriviranje u,a ona za integriranje u/(u^2+9)^2 što neće biti problem integrirati jer metoda supstitucije obavlja posao na trivijalan način.
Wink

BTW,Sveky,jedna preporuka-imaš zbirku od Apsena number 2 gdje ti autor postupno rješava svakakve oblike integrala,zbirka je i više no pedagoška jer ti proda postupak rješavanja pojedinog integrala i onda nakon usvajanja finte rješavaš dalje,svaki put kada se pojavi integral sa novom fintom autor ti to lijepo objelodani tak da nemaš nikakvog beda.
Nakon što polomiš Apsena slijedi finalni meč Very Happy sa legendarnim rusom Demidovičem.
Nakon takva drilanja spreman si se suočiti sa svakim integralom,uživaj.



_________________
Samo sam jedan čovjek,
samo jedan pakao.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
veky
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Sarma = la pohva - posuda
22 = 24 - 2
Lokacija: negdje daleko...
PostPostano: 8:42 sri, 15. 9. 2004    Naslov: Re: novi integral Citirajte i odgovorite
[quote="Vincent Van Ear"]Nakon takva drilanja spreman si se suočiti sa svakim integralom,uživaj.[/quote]

Samo ti sanjaj... :-p

Apsen i Demidovič su legendarni za "drilanje", ali gornja rečenica je ipak malo presamouvjerena, kao što lijepo pokazuje jedan od famoznih zadataka T.Šikića:
[latex]\int_1^5e^{\lfloor x\rfloor}dx[/latex]
(-;
Vincent Van Ear (napisa):
Nakon takva drilanja spreman si se suočiti sa svakim integralom,uživaj.


Samo ti sanjaj... :-p

Apsen i Demidovič su legendarni za "drilanje", ali gornja rečenica je ipak malo presamouvjerena, kao što lijepo pokazuje jedan od famoznih zadataka T.Šikića:

(-;


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
Vincent Van Ear
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
Sarma = la pohva - posuda
-1 = 1 - 2
PostPostano: 9:24 sri, 15. 9. 2004    Naslov: Citirajte i odgovorite
[quote]Samo ti sanjaj... :-p [/quote]

Snovi najčešće vrijede tek kad s tobom osijede…rekao je više puta jedan od najvećih ''balkanskih'' pjevača;)

[quote]Apsen i Demidovič su legendarni za "drilanje", ali gornja rečenica je ipak malo presamouvjerena, kao što lijepo pokazuje jedan od famoznih zadataka T.Šikića:

(-; [/quote]

Hm,nebi li to ovako išlo:

[color=green]1S5 e^int(x) = 1S2 e^1 dx + 2S3 e^2 dx + 3S4 e^3 dx + 4S5 e^4 dx[/color]

Naravno,vjerojatno ne'jde tako jer bi to bilo suviše jednostavno,a ipak je tim primjerom Veky:P htio spustiti moju(priznajem,nezasluženu) samouvjerenost.;)
I naravno,Veky nebi škodilo da nam prezentiraš rješenje,makar mrvice pa ćemo mi dalje mjesiti to tijesto.=))
Citat:
Samo ti sanjaj... :-p


Snovi najčešće vrijede tek kad s tobom osijede…rekao je više puta jedan od najvećih ''balkanskih'' pjevačaWink

Citat:
Apsen i Demidovič su legendarni za "drilanje", ali gornja rečenica je ipak malo presamouvjerena, kao što lijepo pokazuje jedan od famoznih zadataka T.Šikića:

(-;


Hm,nebi li to ovako išlo:

1S5 e^int(x) = 1S2 e^1 dx + 2S3 e^2 dx + 3S4 e^3 dx + 4S5 e^4 dx

Naravno,vjerojatno ne'jde tako jer bi to bilo suviše jednostavno,a ipak je tim primjerom Veky:P htio spustiti moju(priznajem,nezasluženu) samouvjerenost.Wink
I naravno,Veky nebi škodilo da nam prezentiraš rješenje,makar mrvice pa ćemo mi dalje mjesiti to tijesto.=))



_________________
Samo sam jedan čovjek,
samo jedan pakao.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
veky
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Sarma = la pohva - posuda
22 = 24 - 2
Lokacija: negdje daleko...
PostPostano: 10:42 sri, 15. 9. 2004    Naslov: Citirajte i odgovorite
[quote="Vincent Van Ear"][quote]Samo ti sanjaj... :-p [/quote]

Snovi najčešće vrijede tek kad s tobom osijede…rekao je više puta jedan od najvećih ''balkanskih'' pjevača;)[/quote]

Naravno. A bar smo mi imali one snove koji se teško ostvare... ;-)

[quote][quote]Apsen i Demidovič su legendarni za "drilanje", ali gornja rečenica je ipak malo presamouvjerena, kao što lijepo pokazuje jedan od famoznih zadataka T.Šikića:

(-; [/quote]

Hm,nebi li to ovako išlo:

[color=green]1S5 e^int(x) = 1S2 e^1 dx + 2S3 e^2 dx + 3S4 e^3 dx + 4S5 e^4 dx[/color]

Naravno,vjerojatno ne'jde tako jer bi to bilo suviše jednostavno,a ipak je tim primjerom Veky:P htio spustiti moju(priznajem,nezasluženu) samouvjerenost.;)[/quote]

Ne. To ide točno tako. Nije mi uopće bio cilj spustiti tvoju samouvjerenost, već istaknuti da Demidovič i Apsen nemaju veze s takvim zadacima. Mislim da ćeš se složiti da netko čiji se susret s integralima svodio samo na gore navedene drilere, može samo zbunjeno buljiti u ovaj integral. :-)

[quote]I naravno,Veky nebi škodilo da nam prezentiraš rješenje,makar mrvice pa ćemo mi dalje mjesiti to tijesto.=))[/quote]

[latex]\frac{e^5-e}{e-1}[/latex] :-)
Vincent Van Ear (napisa):
Citat:
Samo ti sanjaj... :-p


Snovi najčešće vrijede tek kad s tobom osijede…rekao je više puta jedan od najvećih ''balkanskih'' pjevačaWink


Naravno. A bar smo mi imali one snove koji se teško ostvare... Wink

Citat:
Citat:
Apsen i Demidovič su legendarni za "drilanje", ali gornja rečenica je ipak malo presamouvjerena, kao što lijepo pokazuje jedan od famoznih zadataka T.Šikića:

(-;


Hm,nebi li to ovako išlo:

1S5 e^int(x) = 1S2 e^1 dx + 2S3 e^2 dx + 3S4 e^3 dx + 4S5 e^4 dx

Naravno,vjerojatno ne'jde tako jer bi to bilo suviše jednostavno,a ipak je tim primjerom Veky:P htio spustiti moju(priznajem,nezasluženu) samouvjerenost.Wink


Ne. To ide točno tako. Nije mi uopće bio cilj spustiti tvoju samouvjerenost, već istaknuti da Demidovič i Apsen nemaju veze s takvim zadacima. Mislim da ćeš se složiti da netko čiji se susret s integralima svodio samo na gore navedene drilere, može samo zbunjeno buljiti u ovaj integral. Smile

Citat:
I naravno,Veky nebi škodilo da nam prezentiraš rješenje,makar mrvice pa ćemo mi dalje mjesiti to tijesto.=))


Smile


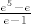
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
Vincent Van Ear
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
Sarma = la pohva - posuda
-1 = 1 - 2
PostPostano: 11:26 sri, 15. 9. 2004    Naslov: Citirajte i odgovorite
[quote]Naravno. A bar smo mi imali one snove koji se teško ostvare... [/quote]

A vidi,vidi,i ti ga slušaš.

[quote]Ne. To ide točno tako. Nije mi uopće bio cilj spustiti tvoju samouvjerenost, već istaknuti da Demidovič i Apsen nemaju veze s takvim zadacima. Mislim da ćeš se složiti da netko čiji se susret s integralima svodio samo na gore navedene drilere, može samo zbunjeno buljiti u ovaj integral. [/quote]

Ha!Sjetiš se vremena kada si ''brstio'' te zadatke…e to su bila vremena…davna=)))

Pa je.;)



Ne dopuštam zbunjivanje mene i drugih:PPP,molit ću lijepo:
e^5-e/e-1 = e*(e^4 – 1)/e-1 = e*(e-1)*(e^3 + e^2 + e + 1) / (e-1)

;))
Citat:
Naravno. A bar smo mi imali one snove koji se teško ostvare...


A vidi,vidi,i ti ga slušaš.

Citat:
Ne. To ide točno tako. Nije mi uopće bio cilj spustiti tvoju samouvjerenost, već istaknuti da Demidovič i Apsen nemaju veze s takvim zadacima. Mislim da ćeš se složiti da netko čiji se susret s integralima svodio samo na gore navedene drilere, može samo zbunjeno buljiti u ovaj integral.


Ha!Sjetiš se vremena kada si ''brstio'' te zadatke…e to su bila vremena…davna=)))

Pa je.Wink



Ne dopuštam zbunjivanje mene i drugih:PPP,molit ću lijepo:
e^5-e/e-1 = e*(e^4 – 1)/e-1 = e*(e-1)*(e^3 + e^2 + e + 1) / (e-1)

Wink)



_________________
Samo sam jedan čovjek,
samo jedan pakao.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
SvekY
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 21. 11. 2003. (23:44:22)
Postovi: (FF)16
Spol: muško
Sarma = la pohva - posuda
11 = 14 - 3
Lokacija: unitarni vektorski prostor
PostPostano: 14:21 sri, 15. 9. 2004    Naslov: Re: novi integral Citirajte i odgovorite
[quote="ZELENIZUBNAPLANETIDOSADE"][quote="SvekY"]Dobio sam integral od [b]1/ ( (u^2+9)^2 )[/b] po u.

Kako dalje? :?:[/quote]
:-k [b]mislis[/b]...
[latex]\displaystyle \int \frac{du}{(u^2+9)^2}[/latex]
:? ?[/quote]
A ja [b]mislim[/b] da moram naucit LaTex.
ZELENIZUBNAPLANETIDOSADE (napisa):
SvekY (napisa):
Dobio sam integral od 1/ ( (u^2+9)^2 ) po u.

Kako dalje? Question

Think mislis...

Confused ?

A ja mislim da moram naucit LaTex.



_________________
Šarm je kad dobijete ono što želite a da to ne morate tražiti. (iz SvekYeve knjige aforizama)
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
veky
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Sarma = la pohva - posuda
22 = 24 - 2
Lokacija: negdje daleko...
PostPostano: 14:40 sri, 15. 9. 2004    Naslov: Re: novi integral Citirajte i odgovorite
[quote="SvekY"][quote="ZELENIZUBNAPLANETIDOSADE"][quote="SvekY"]Dobio sam integral od [b]1/ ( (u^2+9)^2 )[/b] po u.

Kako dalje? :?:[/quote]
:-k [b]mislis[/b]...
[latex]\displaystyle \int \frac{du}{(u^2+9)^2}[/latex]
:? ?[/quote]
A ja [b]mislim[/b] da moram naucit LaTex.[/quote]

Za početak nauči kako se piše. LaTeX . ;-)
SvekY (napisa):
ZELENIZUBNAPLANETIDOSADE (napisa):
SvekY (napisa):
Dobio sam integral od 1/ ( (u^2+9)^2 ) po u.

Kako dalje? Question

Think mislis...

Confused ?

A ja mislim da moram naucit LaTex.


Za početak nauči kako se piše. LaTeX . Wink


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Sarma = la pohva - posuda
7 = 12 - 5
Lokacija: hm?
PostPostano: 15:56 čet, 16. 9. 2004    Naslov: Re: novi integral Citirajte i odgovorite
[quote="SvekY"][quote="ZELENIZUBNAPLANETIDOSADE"][quote="SvekY"]Dobio sam integral od [b]1/ ( (u^2+9)^2 )[/b] po u.

Kako dalje? :?:[/quote]
:-k [b]mislis[/b]...
[latex]\displaystyle \int \frac{du}{(u^2+9)^2}[/latex]
:? ?[/quote]
A ja [b]mislim[/b] da moram naucit LaTex.[/quote]
;) treba ti 20min i prolazak kroz [url=http://degiorgi.math.hr/forum/viewtopic.php?t=2474]uvodni clanak o phpbblatexu[/url] :) imas par linkova i nekoliko osnovnih uputa sa kojima mozes napisati 90% formula koje zazelis :)
(isto tako, latex kod svake formule mozes doznati jednostrukim klikom na doticnu formulu, tako da.. :))
SvekY (napisa):
ZELENIZUBNAPLANETIDOSADE (napisa):
SvekY (napisa):
Dobio sam integral od 1/ ( (u^2+9)^2 ) po u.

Kako dalje? Question

Think mislis...

Confused ?

A ja mislim da moram naucit LaTex.

Wink treba ti 20min i prolazak kroz uvodni clanak o phpbblatexu Smile imas par linkova i nekoliko osnovnih uputa sa kojima mozes napisati 90% formula koje zazelis Smile
(isto tako, latex kod svake formule mozes doznati jednostrukim klikom na doticnu formulu, tako da.. Smile)



_________________

Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk Wink
[Vrh]
Korisnički profil Pošaljite privatnu poruku Posjetite Web stranice
Gost
PostPostano: 0:07 uto, 21. 9. 2004    Naslov: Citirajte i odgovorite
Integral od x^x*(1+lnx),što je onda na kraju rješenje toga integrala,ovo:
e^2ln2 :?:
Integral od x^x*(1+lnx),što je onda na kraju rješenje toga integrala,ovo:
e^2ln2 Question


[Vrh]
Crni
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: muško
Sarma = la pohva - posuda
4 = 29 - 25
Lokacija: Zagreb
PostPostano: 10:17 uto, 21. 9. 2004    Naslov: Citirajte i odgovorite
Rješenje je

[latex]x^{x}+C[/latex]
Rješenje je



[Vrh]
Korisnički profil Pošaljite privatnu poruku
ahri
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
Sarma = la pohva - posuda
7 = 7 - 0
PostPostano: 0:44 sri, 22. 9. 2004    Naslov: Citirajte i odgovorite
a) to je vec receno
b) nisi pokazao kako to integrirati
a) to je vec receno
b) nisi pokazao kako to integrirati



_________________
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Crni
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: muško
Sarma = la pohva - posuda
4 = 29 - 25
Lokacija: Zagreb
PostPostano: 13:02 sri, 22. 9. 2004    Naslov: Citirajte i odgovorite
[quote="ahri"]b) nisi pokazao kako to integrirati[/quote]

Pa valjda supstitucijom t=x^x, za boga miloga!

[latex]\displaystyle t=x^{x}\Longrightarrow lnt=xlnx \Longrightarrow \frac{dt}{t}=(lnx+1)dx\Longrightarrow dx=\frac{dt}{x^{x}(lnx+1)}[/latex]

Dakle,

[latex]\displaystyle \int x^{x}(1+lnx)dx=\int dt=t+C=x^{x}+C[/latex]
ahri (napisa):
b) nisi pokazao kako to integrirati


Pa valjda supstitucijom t=x^x, za boga miloga!



Dakle,



[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2 Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan