|
Polazimo od C-problema sa linearnom diferencijalnom jednadjbom:
[latex]\displaystyle \frac{dx}{dt}=a(t)x+b(t) \\ x(t_0)=x_0[/latex]
[quote="nenad"]Najprije treba odrediti OPĆE rješenje HOMEGENE linearne jednadžbe.[/quote]
Dakle:
[latex]\displaystyle $(1) $\frac{dx}{dt}=a(t)x
\\$(2) $ x(t_0)=c~ , ~c \in R[/latex]
Diferencijalna jednadjba (1) je diferencijalna jednadjba sa separiranim varijablama:
[latex]\frac{dx}{dt}=g(t)h(x)$, za $\\
g(t):=a(t) ~ , ~t \in I$ i $ h(x)=x ~ , ~x \in R[/latex]
Pri cemu su obije fje klase C1, dakle mozemo primijeniti zakljucke iz poglavlja o SEP-ODJ. Tocnije, radi se o teoremu 2.4., koji kaze da tada nas (C)-problem (1)+(2) ima jedinstveno, neprosirivo rijesenje i za c=0 je to rjesenje globalno i dano formulom u(t)=0, za t iz I.
Buduci da je h(0)=0 imamo dvije komponente povezanosti rjesenja (|R+ i |R-).
Zbog antisimetricnosti toga preslikavanja sa obzirom na h(x)=x, imamo skoro-pa-isti racun:
U skladu sa oznakama iz poglavlja o SEP-ODJ, def fju [latex]G : I \rightarrow R[/latex] formulom:
[latex]\displaystyle \int_{t_0}^t a(\tau)d\tau~ , ~t \in I[/latex]
te za c>0 fju H:
[latex]\displaystyle \int_c^x \frac{ d \xi }{ h( \xi ) } = \int_c^x \frac{ d \xi }{ \xi }=\ln x-\ln c = \ln \frac xc~ , ~x \in R^+ \\
\Rightarrow H^{-1}(y)=ce^y~ , ~y \in R[/latex]
Dakle (po tm2.4):
[latex]\displaystyle u(t)=H^{-1}(G(t))~ , ~t \in I \Rightarrow u(t)=ce^{\int_{t_0}^t a(\tau)d\tau}~ , ~t \in I[/latex]
Za slucaj c<0 imamo potpuno isti slucaj, dakle, uz oznaku:
[latex]U(t,s)=\int^t_s a(\tau)d\tau~ , ~t,s \in I[/latex]
slijedi da je za bilo koji c iz R rijesenje C-problema dano formulom:
[latex]u(t)=c \cdot U(t, t_0)~ , ~t \in I[/latex]
Izvod formule za rijesenje gornjeg C-problema bazira se na dosjetki zvanoj [b]METODA VARIJACIJE KONSTANTI[/b] koja se bazira na pretpostavci da je c funkcija od t, tj:
[latex](15)$ $u(t)=c(t) \cdot U(t, t_0)~ , ~t \in I[/latex]
Da bi odredili tu fju c(t) treba osigurati da u(t) zadovoljava uvjete C-problema, tj:
[latex]\displaystyle \frac d{dt}c(t)U(t, t_0)=a(t)c(t)U(t,t_0)+b(t) $ i $\\
c(t_0)U(t,t_0)=x_0[/latex]
Raspisemo diferencijal:
[latex]\displaystyle \frac d{dt}c(t)U(t,t_0)=\frac{dc}{dt}(t)U(t,t_0)+c(t)\partial_1U(t,t_0)[/latex]
..koristeci se rezultatima leme 3.3 o svojstvima fje U(t,s) dobivamo jednadjbe:
[latex]\displaystyle \frac{dc}{dt}(t)U(t,t_0)=b(t) $ i $ c(t_0)=x_0[/latex]
mnozimo fju sa [latex]\frac 1{U(t,t_0)}=U(t_0,t)[/latex] i dobivamo:
[latex]\displaystyle \frac{dc}{dt}(t)=U(t_0,t)b(t)~ , ~t \in I[/latex]
Integracijom:
[latex]\displaystyle c(t)-c(t_0)=\int_{t_0}^tU(t_0, \tau)b(\tau)d\tau \\
\Rightarrow c(t)=\int_{t_0}^tU(t_0, \tau)b(\tau)d\tau+x_0[/latex]
Uvrstavajuci u pocetnu pretpostavku (15) dobivamo:
[latex]\displaystyle u(t)=c(t)U(t,t_0)=U(t,t_0)\left[ x_0 + \int_{t_0}^t U(t_0, \tau)b(\tau)d\tau \right][/latex]
..pa mnozeci elemente u zagradama, opet na osnovu leme 3.3 dobivamo:
[latex]\displaystyle u(t)=U(t,t_0)x_0+\int^t_{t_0}U(t,\tau)b(\tau)d\tau~ , ~t \in I[/latex]
...sto je rjesenje iz zakljucka teorema 3.2 o rijesenju c-problema sa L-ODJ
phew :) eto :)
[quote="nenad"][i]ansatz[/i][/quote]
samo ovo ne razumijem :shock: :?
Polazimo od C-problema sa linearnom diferencijalnom jednadjbom:
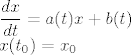
| nenad (napisa): | | Najprije treba odrediti OPĆE rješenje HOMEGENE linearne jednadžbe. |
Dakle:
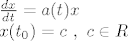
Diferencijalna jednadjba (1) je diferencijalna jednadjba sa separiranim varijablama:
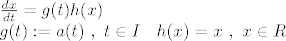
Pri cemu su obije fje klase C1, dakle mozemo primijeniti zakljucke iz poglavlja o SEP-ODJ. Tocnije, radi se o teoremu 2.4., koji kaze da tada nas (C)-problem (1)+(2) ima jedinstveno, neprosirivo rijesenje i za c=0 je to rjesenje globalno i dano formulom u(t)=0, za t iz I.
Buduci da je h(0)=0 imamo dvije komponente povezanosti rjesenja (|R+ i |R-).
Zbog antisimetricnosti toga preslikavanja sa obzirom na h(x)=x, imamo skoro-pa-isti racun:
U skladu sa oznakama iz poglavlja o SEP-ODJ, def fju 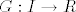 formulom: formulom:
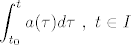
te za c>0 fju H:
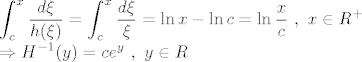
Dakle (po tm2.4):
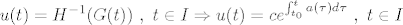
Za slucaj c<0 imamo potpuno isti slucaj, dakle, uz oznaku:
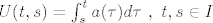
slijedi da je za bilo koji c iz R rijesenje C-problema dano formulom:
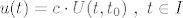
Izvod formule za rijesenje gornjeg C-problema bazira se na dosjetki zvanoj METODA VARIJACIJE KONSTANTI koja se bazira na pretpostavci da je c funkcija od t, tj:
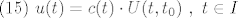
Da bi odredili tu fju c(t) treba osigurati da u(t) zadovoljava uvjete C-problema, tj:
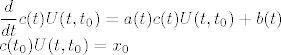
Raspisemo diferencijal:
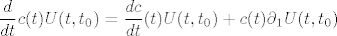
..koristeci se rezultatima leme 3.3 o svojstvima fje U(t,s) dobivamo jednadjbe:
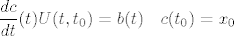
mnozimo fju sa 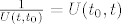 i dobivamo: i dobivamo:
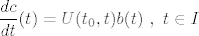
Integracijom:
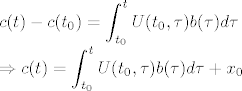
Uvrstavajuci u pocetnu pretpostavku (15) dobivamo:
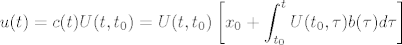
..pa mnozeci elemente u zagradama, opet na osnovu leme 3.3 dobivamo:
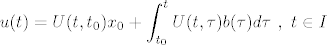
...sto je rjesenje iz zakljucka teorema 3.2 o rijesenju c-problema sa L-ODJ
phew  eto eto 
samo ovo ne razumijem  
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |





