| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
banank0
Forumaš(ica)
Pridružen/a: 11. 06. 2013. (13:36:04)
Postovi: (25)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 18:54 pon, 24. 3. 2014 Naslov: Postano: 18:54 pon, 24. 3. 2014 Naslov: |
    |
|
|
Evo npr. pod (g). Iskoristimo jednakost iz (a), tj. pokazimo da je
[tex] \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} ) = \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex].
Inkluzija [tex] \supset [/tex] je jasna. Naime, zbog [tex] \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} \supset \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} [/tex] je onda i [tex] \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} ) \supset \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex].
Da bismo pokazali da vrijedi inkluzija [tex] \subset [/tex], pokazimo da je [tex] \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} \subset \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex], jer cemo onda imati i [tex] \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} ) \subset \sigma( \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) ) = \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex]. Neka je zato [tex] \langle c,d \rangle \in \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} [/tex]. Iskoristimo sada cinjenicu da postoji niz racionalnih brojeva [tex](c_n) \subset \mathbb{Q} [/tex] takav da [tex]c_n \searrow c[/tex] (tj., tezi ka [tex]c[/tex] zdesna), i postoji niz racionalnih brojeva [tex](d_n) \subset \mathbb{Q} [/tex] takav da [tex]d_n \nearrow d[/tex] (tj., tezi ka [tex]d[/tex] slijeva).
Uocimo da je [tex]\displaystyle \bigcup_{n=1}^\infty \langle c_n,d_n \rangle = \langle c,d \rangle. [/tex] Buduci da je svaki [tex]\langle c_n,d_n \rangle[/tex] element skupa [tex] \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} [/tex], a [tex]\sigma[/tex]-algebra je zatvorena na prebrojive unije, zakljucujemo da je [tex]\langle c,d \rangle \in \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex].
Dakle, [tex] \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} \subset \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex], pa slijedi trazena inkluzija, odnosno jednakost.
(Slicno ovome, zadatak pod (d) slijedi iz (e) dijela.)
Evo npr. pod (g). Iskoristimo jednakost iz (a), tj. pokazimo da je
[tex] \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} ) = \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex].
Inkluzija [tex] \supset [/tex] je jasna. Naime, zbog [tex] \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} \supset \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} [/tex] je onda i [tex] \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} ) \supset \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex].
Da bismo pokazali da vrijedi inkluzija [tex] \subset [/tex], pokazimo da je [tex] \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} \subset \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex], jer cemo onda imati i [tex] \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} ) \subset \sigma( \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) ) = \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex]. Neka je zato [tex] \langle c,d \rangle \in \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} [/tex]. Iskoristimo sada cinjenicu da postoji niz racionalnih brojeva [tex](c_n) \subset \mathbb{Q} [/tex] takav da [tex]c_n \searrow c[/tex] (tj., tezi ka [tex]c[/tex] zdesna), i postoji niz racionalnih brojeva [tex](d_n) \subset \mathbb{Q} [/tex] takav da [tex]d_n \nearrow d[/tex] (tj., tezi ka [tex]d[/tex] slijeva).
Uocimo da je [tex]\displaystyle \bigcup_{n=1}^\infty \langle c_n,d_n \rangle = \langle c,d \rangle. [/tex] Buduci da je svaki [tex]\langle c_n,d_n \rangle[/tex] element skupa [tex] \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} [/tex], a [tex]\sigma[/tex]-algebra je zatvorena na prebrojive unije, zakljucujemo da je [tex]\langle c,d \rangle \in \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex].
Dakle, [tex] \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{R} \} \subset \sigma( \{ \langle a,b \rangle \ \mid \ a,b \in \mathbb{Q} \} ) [/tex], pa slijedi trazena inkluzija, odnosno jednakost.
(Slicno ovome, zadatak pod (d) slijedi iz (e) dijela.)
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 15:13 čet, 21. 8. 2014 Naslov: Postano: 15:13 čet, 21. 8. 2014 Naslov: |
    |
|
|
Misli se na Carathéodoryjev teorem, tj. teorem [tex]3. 14[/tex].
Naime, [tex]m^*[/tex] je vanjska mjera (definicija [tex]3. 10[/tex]), a skup ([tex]m^*[/tex]-)izmjerivih skupova označava se sa [tex]\mathcal{M}_{m^*}[/tex] (označeno i s [tex](3. 13)[/tex] u skripti). Pitanje u kolokviju odnosi se na, u Carathéodoryjevom teoremu, definiranu funkciju [tex]m := m^*|_{\mathcal{M}_{m^*}}[/tex] - što teorem doslovno tvrdi: to preslikavanje, definirano preko vanjske mjere, a restringirano (tj. definirano) na izmjerivim skupovima, je mjera!
Misli se na Carathéodoryjev teorem, tj. teorem [tex]3. 14[/tex].
Naime, [tex]m^*[/tex] je vanjska mjera (definicija [tex]3. 10[/tex]), a skup ([tex]m^*[/tex]-)izmjerivih skupova označava se sa [tex]\mathcal{M}_{m^*}[/tex] (označeno i s [tex](3. 13)[/tex] u skripti). Pitanje u kolokviju odnosi se na, u Carathéodoryjevom teoremu, definiranu funkciju [tex]m := m^*|_{\mathcal{M}_{m^*}}[/tex] - što teorem doslovno tvrdi: to preslikavanje, definirano preko vanjske mjere, a restringirano (tj. definirano) na izmjerivim skupovima, je mjera!
|
|
| [Vrh] |
|
Gost
|
 Postano: 15:35 čet, 21. 8. 2014 Naslov: Postano: 15:35 čet, 21. 8. 2014 Naslov: |
    |
|
|
[quote="Phoenix"]Misli se na Carathéodoryjev teorem, tj. teorem [tex]3. 14[/tex].
Naime, [tex]m^*[/tex] je vanjska mjera (definicija [tex]3. 10[/tex]), a skup ([tex]m^*[/tex]-)izmjerivih skupova označava se sa [tex]\mathcal{M}_{m^*}[/tex] (označeno i s [tex](3. 13)[/tex] u skripti). Pitanje u kolokviju odnosi se na, u Carathéodoryjevom teoremu, definiranu funkciju [tex]m := m^*|_{\mathcal{M}_{m^*}}[/tex] - što teorem doslovno tvrdi: to preslikavanje, definirano preko vanjske mjere, a restringirano (tj. definirano) na izmjerivim skupovima, je mjera![/quote]
hvala!
| Phoenix (napisa): | Misli se na Carathéodoryjev teorem, tj. teorem [tex]3. 14[/tex].
Naime, [tex]m^*[/tex] je vanjska mjera (definicija [tex]3. 10[/tex]), a skup ([tex]m^*[/tex]-)izmjerivih skupova označava se sa [tex]\mathcal{M}_{m^*}[/tex] (označeno i s [tex](3. 13)[/tex] u skripti). Pitanje u kolokviju odnosi se na, u Carathéodoryjevom teoremu, definiranu funkciju [tex]m := m^*|_{\mathcal{M}_{m^*}}[/tex] - što teorem doslovno tvrdi: to preslikavanje, definirano preko vanjske mjere, a restringirano (tj. definirano) na izmjerivim skupovima, je mjera! |
hvala!
|
|
| [Vrh] |
|
mango
Forumaš(ica)

Pridružen/a: 02. 02. 2012. (21:26:21)
Postovi: (F)16
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 18:01 ned, 31. 8. 2014 Naslov: Postano: 18:01 ned, 31. 8. 2014 Naslov: |
    |
|
|
[quote="mango"]3. http://web.math.pmf.unizg.hr/nastava/mii/files/mi-zav-2008.pdf 1.b) zad[/quote]
[quote="Vip"]3. i ja bih voljela pomoć oko toga ako netko zna..?[/quote]
Ovdje se zapravo misli na sljedeci dovoljni uvjet:
skupovna funkcija [latex]\mu\colon\mathcal{R}\to[0,+\infty][/latex] je sigma-aditivna i prsten [latex]\mathcal{R}[/latex] zadovoljava uvjet [latex](3.8)[/latex].
Dokaz se sastoji od sljedeceg:
- provjeriti da je formulom [latex](3.9)[/latex] doista dana jedna vanjska mjera [latex]\mu^\ast\colon\mathcal{P}(X)\to[0,+\infty][/latex]
- i provjeriti da je restrikcija od [latex]\mu^\ast[/latex] na [latex]\mathcal{R}[/latex] upravo polazna skupovna funkcija [latex]\mu[/latex].
Oboje je lagano. Ovo drugo je komentirano u dokazu Korolara 3.16., to je zapravo druga tocka u tom korolaru.
To je bio najlogicniji moguci odgovor. Naravno da se mogu postaviti i neki umjetni trivijalni dovoljni uvjeti, ali mislilo se na nesto od gradiva s predavanja.
[size=9][color=#999999]Added after 12 minutes:[/color][/size]
[quote="mango"]4. http://web.math.pmf.unizg.hr/nastava/mii/files/mi-kol1-2010-rj.pdf 2.zad[/quote]
[quote="Vip"]4. Pogledaj malo primjer 2.9[/quote]
U Primjeru 2.9 je zapravo samo komentirano da se konacna aditivnost vidi jednako lako kao i u jednoj dimenziji.
Potom jos trebati dokazati sigma-aditivnost i prilagoditi dokaz Leme 2.10 u dvije dimenzije, ali to ide toliko direktno, da gotovo nista ne treba mijenjati, samo spominjete pravokutnike iz [latex]R\in\mathcal{I}^2[/latex], umjesto intervala [latex]I\in\mathcal{I}^1[/latex].
Dakle, pisuci [latex]R[/latex] umjesto [latex]I_1\times I_2[/latex] si dosta skratite i taj dio dokaza postaje gotovo upravo isti kao Lema 2.10.
| Vip (napisa): | | 3. i ja bih voljela pomoć oko toga ako netko zna..? |
Ovdje se zapravo misli na sljedeci dovoljni uvjet:
skupovna funkcija 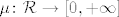 je sigma-aditivna i prsten je sigma-aditivna i prsten 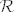 zadovoljava uvjet zadovoljava uvjet 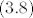 . .
Dokaz se sastoji od sljedeceg:
- provjeriti da je formulom 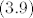 doista dana jedna vanjska mjera doista dana jedna vanjska mjera 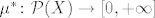
- i provjeriti da je restrikcija od 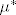 na na 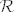 upravo polazna skupovna funkcija upravo polazna skupovna funkcija 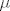 . .
Oboje je lagano. Ovo drugo je komentirano u dokazu Korolara 3.16., to je zapravo druga tocka u tom korolaru.
To je bio najlogicniji moguci odgovor. Naravno da se mogu postaviti i neki umjetni trivijalni dovoljni uvjeti, ali mislilo se na nesto od gradiva s predavanja.
Added after 12 minutes:
| Vip (napisa): | | 4. Pogledaj malo primjer 2.9 |
U Primjeru 2.9 je zapravo samo komentirano da se konacna aditivnost vidi jednako lako kao i u jednoj dimenziji.
Potom jos trebati dokazati sigma-aditivnost i prilagoditi dokaz Leme 2.10 u dvije dimenzije, ali to ide toliko direktno, da gotovo nista ne treba mijenjati, samo spominjete pravokutnike iz 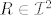 , umjesto intervala , umjesto intervala  . .
Dakle, pisuci 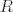 umjesto umjesto 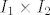 si dosta skratite i taj dio dokaza postaje gotovo upravo isti kao Lema 2.10. si dosta skratite i taj dio dokaza postaje gotovo upravo isti kao Lema 2.10.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 17:00 uto, 2. 9. 2014 Naslov: Postano: 17:00 uto, 2. 9. 2014 Naslov: |
    |
|
|
[quote="Anonymous"]Moze pomoc oko ovogodisnjeg drugog kolokvija? http://web.math.pmf.unizg.hr/nastava/mii/files/mii_2014_kol2_rj.pdf
Nije mi jasno u 3.a) kako dodjemo do sume integrala? Ako bi netko bio voljan prokomentirat rjesenje.. :)[/quote]
[latex]\displaystyle\int_{\mathbb{R}}g_a^+ \,d\lambda=\int_{1}^\infty g_a^+(x) \,dx=\lim_{n\to \infty}\int_{1}^{n} g_a^+(x) \,dx=\lim_{n\to \infty} \sum_{k=1}^{n-1} \int_{k}^{k+1} a^k \cdot 1_{[k,k+1/2\rangle}(x)\,dx[/latex]
Detaljno korak po korak:
- U prvoj jednakosti smo presli s Lebesgueovog na nepravi Riemannov integral. Mozda je malo zbunjujuce bilo sto je i dalje pisao integral po Lebesgueovoj mjeri, shvatimo ga radije kao Riemannov.
- U drugoj jednakosti smo samo po definiciji raspisali nepravi Riemannov integral. Gornja granica n zapravo moze biti i realan broj, ali posebno moze biti bas prirodan, cime dobivamo limes niza, umjesto opcenitijeg limesa funkcije.
- U trecoj jednakosti je interval integracije [1,n] rastavljen na integrale po intervalima [k,k+1] (intervalima duljine 1) te je iskoristena tzv. aditivnost Riemannovog integrala po podrucju integracije. Odatle suma. Istovremeno je i uvrsten dani izraz za funkciju na intervalu [k,k+1].
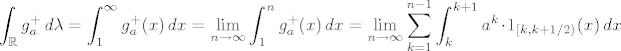
Detaljno korak po korak:
- U prvoj jednakosti smo presli s Lebesgueovog na nepravi Riemannov integral. Mozda je malo zbunjujuce bilo sto je i dalje pisao integral po Lebesgueovoj mjeri, shvatimo ga radije kao Riemannov.
- U drugoj jednakosti smo samo po definiciji raspisali nepravi Riemannov integral. Gornja granica n zapravo moze biti i realan broj, ali posebno moze biti bas prirodan, cime dobivamo limes niza, umjesto opcenitijeg limesa funkcije.
- U trecoj jednakosti je interval integracije [1,n] rastavljen na integrale po intervalima [k,k+1] (intervalima duljine 1) te je iskoristena tzv. aditivnost Riemannovog integrala po podrucju integracije. Odatle suma. Istovremeno je i uvrsten dani izraz za funkciju na intervalu [k,k+1].
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Rhodia
Forumaš(ica)
Pridružen/a: 01. 10. 2013. (20:14:50)
Postovi: (D)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 14:32 uto, 3. 4. 2018 Naslov: Re: zatvorenost na razlike u prstenu Postano: 14:32 uto, 3. 4. 2018 Naslov: Re: zatvorenost na razlike u prstenu |
    |
|
|
[quote="Rhodia"]
Recimo da imamo familiju F. Neka su A, B iz F.
Skupovno je A\B podskup od A koji je iz F. Je li onda uvjet "zatvorenosti na razlike" trivijalno uvijek zadovoljen?
[/quote]
Koliko shvaćam, tvrdnja u pozadini je (unutar nekog univerzalnog skupa [latex]X[/latex])
[latex]\left( \forall A \in \mathcal{F} \right) \left( \forall B \subseteq X \right) \left( B \subseteq A \Rightarrow B \in \mathcal{F} \right),[/latex]
što nije točno; zapravo i ne vidim motivaciju za ovakvim razmišljanjem i tvrdnjom. Zašto bi svaki podskup iz neke "dobre" familije opet bio "dobar" (odnosno zadržavao za nas "dobro" svojstvo)? :?:
[quote="Rhodia"]
Pretpostavljam da to nije slučaj - pada mi na pamet familija otvorenih skupova u R^2. Neka je A = R^2 i neka je B = K(0,1).
A\B je zatvoren skup pa nije iz familije otvorenih skupova u R^2 (ali je skupovno A\B sadržan u A)
Što se unije tiče ta je familija zatvorena na unije (proizvoljna unije otvorenih je otvoren skup), ali nije prsten jer nije zatvorena na razliku.
[/quote]
Tako je; ovo je obrazloženje zašto familija otvorenih skupova nije prsten. No time niste opovrgnuli gore naslućenu tvrdnju; treba Vam familija koja je prsten, ali nije točno da sadrži sve podskupove svojih elemenata.
| Rhodia (napisa): |
Recimo da imamo familiju F. Neka su A, B iz F.
Skupovno je A\B podskup od A koji je iz F. Je li onda uvjet "zatvorenosti na razlike" trivijalno uvijek zadovoljen?
|
Koliko shvaćam, tvrdnja u pozadini je (unutar nekog univerzalnog skupa  ) )
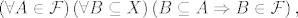
što nije točno; zapravo i ne vidim motivaciju za ovakvim razmišljanjem i tvrdnjom. Zašto bi svaki podskup iz neke "dobre" familije opet bio "dobar" (odnosno zadržavao za nas "dobro" svojstvo)? 
| Rhodia (napisa): |
Pretpostavljam da to nije slučaj - pada mi na pamet familija otvorenih skupova u R^2. Neka je A = R^2 i neka je B = K(0,1).
A\B je zatvoren skup pa nije iz familije otvorenih skupova u R^2 (ali je skupovno A\B sadržan u A)
Što se unije tiče ta je familija zatvorena na unije (proizvoljna unije otvorenih je otvoren skup), ali nije prsten jer nije zatvorena na razliku.
|
Tako je; ovo je obrazloženje zašto familija otvorenih skupova nije prsten. No time niste opovrgnuli gore naslućenu tvrdnju; treba Vam familija koja je prsten, ali nije točno da sadrži sve podskupove svojih elemenata.
_________________
Mario Stipčić
|
|
| [Vrh] |
|
|










