| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
student
Forumaš(ica)


Pridružen/a: 03. 04. 2003. (13:18:57)
Postovi: (B)16
Lokacija: praktikum 3
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 12:11 pet, 24. 9. 2004 Naslov: Re: logaritmi i rang Postano: 12:11 pet, 24. 9. 2004 Naslov: Re: logaritmi i rang |
    |
|
|
[quote="student"]pozdrav
muce me 2 pitanja:
1. kako odabrati koju granu logaritma izbaciti u zadacima kod funkcija operatora? moze par
rijeci o tome, to me jako muci.[/quote]
Biraš bilo koju "granu" (plohu) čiji branch cut ne prolazi kroz nijednu svojstvenu vrijednost.
Odnosno, izbacuješ bilo koju zraku koja ne prolazi kroz nijednu svojstvenu vrijednost. Jer je svojstvenih vrijednosti u našem slučaju samo konačno mnogo, uvijek takva postoji. (Osim ako je 0 svojstvena vrijednost, no traženje lna singularnog operatora je ionako izazivanje vraga: ).
(vsego, "izazivanje vraga" je fraza, i sumnjam da se u njoj druga riječ treba pisati velikim slovom. No ako želiš...: )
Note: ne izbacuješ grane logaritma - ostalo bi ti premalo toga:-). Izbacuješ neku zraku iz ishodišta, koja odgovara odabiranju kuta koji će biti argument brojevima na rubu definicije logaritma.
Ono što se često ne naglasi, i zato stvara zabunu kod dosta studenata, je da je potpuno svejedno koja se zraka izbaci, _dok god se u tome bude konzistentan_ (tijekom jednog zadatka). Npr. ako imaš svojstvene vrijednosti 2i i -3 , možeš izbaciti zraku koja prolazi kroz 1 . Ili zraku koja prolazi kroz i-1 . Ili neku treću. No bitno je da klizne argumente (i pomoću njih logaritme) svih svojstvenih vrijednosti (i drugih stvari koje ti trebaju u zadatku) izračunaš pomoću te iste grane.
[quote]2. V je realan v.p. dimV > 2, T iz L(V) takav da je r(T+I)=2. sto mozemo iz toga zakljuciti o T?[/quote]
Puno lipih stvari. :-D
Zezam se... mislim da je pitanje neprecizno.
Npr. dimenzija slike od T+I je 2 . To znači da npr. postoje dva nezavisna vektora, a i b , takva da je, za svaki x@V , (T+I)(x)=Tx+x , linearna kombinacija od a i b . Ako skup {a,b} nadopunimo do baze (bar jednim vektorom, jer je dimV>2 ), bit će matrični zapis operatora T+I u toj bazi matrica s 2 reda nekih koeficijenata (u onim linearnim kombinacijama a i b za T(vektore baze) ), a ostali redovi će biti nule. Matrica od I u svakoj bazi (pa i u toj) je jedinična matrica, pa je dakle matrica od T nešto što od 3. reda nadalje ima -1ice po dijagonali. To između ostalog znači da je zadnjih n-2 reda nezavisno, pa je r(T)>=n-2 . No to je samo jedna vrsta zaključaka... (drugi bi možda išli along the line svojstvenih vrijednosti...) dok ne kažeš što točno misliš s pitanjem, teško je biti precizniji.
HTH,
| student (napisa): | pozdrav
muce me 2 pitanja:
1. kako odabrati koju granu logaritma izbaciti u zadacima kod funkcija operatora? moze par
rijeci o tome, to me jako muci. |
Biraš bilo koju "granu" (plohu) čiji branch cut ne prolazi kroz nijednu svojstvenu vrijednost.
Odnosno, izbacuješ bilo koju zraku koja ne prolazi kroz nijednu svojstvenu vrijednost. Jer je svojstvenih vrijednosti u našem slučaju samo konačno mnogo, uvijek takva postoji. (Osim ako je 0 svojstvena vrijednost, no traženje lna singularnog operatora je ionako izazivanje vraga: ).
(vsego, "izazivanje vraga" je fraza, i sumnjam da se u njoj druga riječ treba pisati velikim slovom. No ako želiš...: )
Note: ne izbacuješ grane logaritma - ostalo bi ti premalo toga:-). Izbacuješ neku zraku iz ishodišta, koja odgovara odabiranju kuta koji će biti argument brojevima na rubu definicije logaritma.
Ono što se često ne naglasi, i zato stvara zabunu kod dosta studenata, je da je potpuno svejedno koja se zraka izbaci, _dok god se u tome bude konzistentan_ (tijekom jednog zadatka). Npr. ako imaš svojstvene vrijednosti 2i i -3 , možeš izbaciti zraku koja prolazi kroz 1 . Ili zraku koja prolazi kroz i-1 . Ili neku treću. No bitno je da klizne argumente (i pomoću njih logaritme) svih svojstvenih vrijednosti (i drugih stvari koje ti trebaju u zadatku) izračunaš pomoću te iste grane.
| Citat: | | 2. V je realan v.p. dimV > 2, T iz L(V) takav da je r(T+I)=2. sto mozemo iz toga zakljuciti o T? |
Puno lipih stvari. 
Zezam se... mislim da je pitanje neprecizno.
Npr. dimenzija slike od T+I je 2 . To znači da npr. postoje dva nezavisna vektora, a i b , takva da je, za svaki x@V , (T+I)(x)=Tx+x , linearna kombinacija od a i b . Ako skup {a,b} nadopunimo do baze (bar jednim vektorom, jer je dimV>2 ), bit će matrični zapis operatora T+I u toj bazi matrica s 2 reda nekih koeficijenata (u onim linearnim kombinacijama a i b za T(vektore baze) ), a ostali redovi će biti nule. Matrica od I u svakoj bazi (pa i u toj) je jedinična matrica, pa je dakle matrica od T nešto što od 3. reda nadalje ima -1ice po dijagonali. To između ostalog znači da je zadnjih n-2 reda nezavisno, pa je r(T)>=n-2 . No to je samo jedna vrsta zaključaka... (drugi bi možda išli along the line svojstvenih vrijednosti...) dok ne kažeš što točno misliš s pitanjem, teško je biti precizniji.
HTH,
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 13:14 pet, 24. 9. 2004 Naslov: Re: logaritmi i rang Postano: 13:14 pet, 24. 9. 2004 Naslov: Re: logaritmi i rang |
    |
|
|
[quote="student"]1. kako odabrati koju granu logaritma izbaciti u zadacima kod funkcija operatora? moze par
rijeci o tome, to me jako muci.[/quote]
Logaritam operatora A (zapravo neka određena grana logaritma) ima smisla kad god je spektar od A podskup domene logaritma (zapravo te grane logaritma), tj. nijedna svojstvena vrijednost od A ne leži na izbačenom polupravcu.
Tako da za operator možemo računati razne grane logaritma, i to su (načelno) različiti operatori. (Neki od njih će biti isti, ali neki možda i neće.) Tako da u tom smislu postoji "više logaritama" operatora A. Jedino što im je zajedničko je da je e^(logaritam od A) uvijek jednako A (za svaku granu).
Nema nekog pravila za odabir grane. Ukoliko se (npr. na pismenom) traži logaritam nekog operatora, onda se misli na [i]bilo koju[/i] granu logaritma, tj. kako veky reče, odaberemo neku granu i onda ostanemo dosljedni u daljnjim računima. Dakle, ukoliko na testu ništa ne piše, onda je izbor grane proizvoljan.
Tako npr. ukoliko trebamo naći [i]neki[/i] operator B takav da je e^B=A, onda racunamo [i]bilo koju[/i] granu logaritma B=Ln(A).
Ipak je uobičajeno (ni ovo nije [i]pravilo[/i] ali je standardno) da se glavna grana logaritma (izbačen je nepozitivni dio realne poluosi; argumenti, tj. kutovi, se uvijek uzimaju u [latex]\langle -\pi,\pi\rangle[/latex]) uzima kad god je definirana. Dakle, to je najprirodniji izbor.
Naprimjer, 3^z znači e^(z*Ln(3)), gdje je Ln glavna grana logaritma. Pritom z ne smije biti realni broj <=0.
:prodike:
| student (napisa): | 1. kako odabrati koju granu logaritma izbaciti u zadacima kod funkcija operatora? moze par
rijeci o tome, to me jako muci. |
Logaritam operatora A (zapravo neka određena grana logaritma) ima smisla kad god je spektar od A podskup domene logaritma (zapravo te grane logaritma), tj. nijedna svojstvena vrijednost od A ne leži na izbačenom polupravcu.
Tako da za operator možemo računati razne grane logaritma, i to su (načelno) različiti operatori. (Neki od njih će biti isti, ali neki možda i neće.) Tako da u tom smislu postoji "više logaritama" operatora A. Jedino što im je zajedničko je da je e^(logaritam od A) uvijek jednako A (za svaku granu).
Nema nekog pravila za odabir grane. Ukoliko se (npr. na pismenom) traži logaritam nekog operatora, onda se misli na bilo koju granu logaritma, tj. kako veky reče, odaberemo neku granu i onda ostanemo dosljedni u daljnjim računima. Dakle, ukoliko na testu ništa ne piše, onda je izbor grane proizvoljan.
Tako npr. ukoliko trebamo naći neki operator B takav da je e^B=A, onda racunamo bilo koju granu logaritma B=Ln(A).
Ipak je uobičajeno (ni ovo nije pravilo ali je standardno) da se glavna grana logaritma (izbačen je nepozitivni dio realne poluosi; argumenti, tj. kutovi, se uvijek uzimaju u 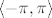 ) uzima kad god je definirana. Dakle, to je najprirodniji izbor. ) uzima kad god je definirana. Dakle, to je najprirodniji izbor.
Naprimjer, 3^z znači e^(z*Ln(3)), gdje je Ln glavna grana logaritma. Pritom z ne smije biti realni broj ⇐0.

Zadnja promjena: vjekovac; 13:21 pet, 24. 9. 2004; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 16:27 ned, 26. 9. 2004 Naslov: Re: logaritmi i rang Postano: 16:27 ned, 26. 9. 2004 Naslov: Re: logaritmi i rang |
    |
|
|
[quote="Anonymous"]da, to je dio jednog zadatka, nastavak glasi (mislim): tr(T+2nI)=n i 1 je svojstvena vrijednost od T. kako glase karakteristicni i minimalni polinom od T?[/quote]
E sad je "slika" potpuna... :)
r(T+I)=2, tj. d(T+I)=n-2>0 (gdje je n=dim(V)) znači da je -1 svojstvena vrijednost od T s geometrijskom kratošću n-2 (pa joj je algebarska kratnost >=n-2). Nadalje je poznato i da je 1 svojstvena vrijednost od T (alg.krat.>=geom.krat.>=1), a da bi bilo ispunjeno tr(T+2nI)=n, tj. tr(T)=n-2n tr(I)=n-2n^2 = zbroj svoj. vrij. (računatih s alg.krat.), mora još i broj
n-2n^2+(n-2)*1-1=-2n^2+2n-3 biti svojstvena vrijednost od T.
Označimo q=-2n^2+2n-3. (Primijetimo da je taj broj <=-3 pa je različit od -1 i 1.)
Zaključujemo da su -1,1,q sve svojstvene vrijednosti od T redom s (geometrijskim=algebarskim) kratnostima n-2,1,1. Zbog jednakosti geom. i alg. kratnosti vidimo da je cijeli prostor direktna suma svojstvenih potprostora od T pa se T može dijagonalizirati, odakle slijedi da mu je minimalni polinom produkt različitih linearnih faktora.
Dakle,
k(x)=(-1)^n (x+1)^(n-2) (x-1) (x-q)
m(x)= (x+1)(x-1)(x-q)
Drugi pristup rješavanju (takvog) zadatka je sljedeći:
Najprije uzmemo n-2 vektora koji cine bazu svojstvenog potprostora od -1 pa ih nadopunimo jednim svojstvenim vektorom od 1 pa još nadopunimo jednim vektorom do baze cijelog prostora.
Matrica u toj bazi ima puno nula (premda ne znamo što piše u zadnjem stupcu), specijalno je gornje-trokutasta, a nepoznatu vrijednost na dijagonali dobijemo iz jednakosti za trag.
Karak. pol. je sada očigledan, a minimalni se provjerava direktnim množenjem (triju) matrica.
[quote]thnx guys, to je sve sto sam htio cut. keep up the good work![/quote]
Nije [i]nas[/i] lako ušutkat... :lol:
| Anonymous (napisa): | | da, to je dio jednog zadatka, nastavak glasi (mislim): tr(T+2nI)=n i 1 je svojstvena vrijednost od T. kako glase karakteristicni i minimalni polinom od T? |
E sad je "slika" potpuna... 
r(T+I)=2, tj. d(T+I)=n-2>0 (gdje je n=dim(V)) znači da je -1 svojstvena vrijednost od T s geometrijskom kratošću n-2 (pa joj je algebarska kratnost >=n-2). Nadalje je poznato i da je 1 svojstvena vrijednost od T (alg.krat.>=geom.krat.>=1), a da bi bilo ispunjeno tr(T+2nI)=n, tj. tr(T)=n-2n tr(I)=n-2n^2 = zbroj svoj. vrij. (računatih s alg.krat.), mora još i broj
n-2n^2+(n-2)*1-1=-2n^2+2n-3 biti svojstvena vrijednost od T.
Označimo q=-2n^2+2n-3. (Primijetimo da je taj broj ⇐-3 pa je različit od -1 i 1.)
Zaključujemo da su -1,1,q sve svojstvene vrijednosti od T redom s (geometrijskim=algebarskim) kratnostima n-2,1,1. Zbog jednakosti geom. i alg. kratnosti vidimo da je cijeli prostor direktna suma svojstvenih potprostora od T pa se T može dijagonalizirati, odakle slijedi da mu je minimalni polinom produkt različitih linearnih faktora.
Dakle,
k(x)=(-1)^n (x+1)^(n-2) (x-1) (x-q)
m(x)= (x+1)(x-1)(x-q)
Drugi pristup rješavanju (takvog) zadatka je sljedeći:
Najprije uzmemo n-2 vektora koji cine bazu svojstvenog potprostora od -1 pa ih nadopunimo jednim svojstvenim vektorom od 1 pa još nadopunimo jednim vektorom do baze cijelog prostora.
Matrica u toj bazi ima puno nula (premda ne znamo što piše u zadnjem stupcu), specijalno je gornje-trokutasta, a nepoznatu vrijednost na dijagonali dobijemo iz jednakosti za trag.
Karak. pol. je sada očigledan, a minimalni se provjerava direktnim množenjem (triju) matrica.
| Citat: | | thnx guys, to je sve sto sam htio cut. keep up the good work! |
Nije nas lako ušutkat... 
|
|
| [Vrh] |
|
|







