| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
markov
Forumaš(ica)

Pridružen/a: 04. 01. 2006. (01:24:33)
Postovi: (121)16
|
 Postano: 11:29 uto, 31. 3. 2020 Naslov: Peti tjedan 2020. - Ford-Fulkersonov algoritam+ Postano: 11:29 uto, 31. 3. 2020 Naslov: Peti tjedan 2020. - Ford-Fulkersonov algoritam+ |
    |
|
|
str. 70 do 84 skripte. Nije stalo u naslov pa dodajem + primjena u problemu dodjeljivanja
Sama ideja algoritma već je iznesena u Primjeru 8 od prošlog tjedna. Teorem 4.1. kaže da ako trenutni tok nije optimalan moguće je naći put povećanja toka i pomoću njega prijeći na bolji tok. To doduše ne znači da će algoritam završiti u konačno mnogo koraka - mogli smo npr. napredovati za 1/2^n u n-toj iteraciji algoritma. Naravno, to nije moguće u mreži s cjelobrojnim kapacitetima, jer je napredak uvijek cjelobrojan ... kako već i piše u skripti ...
No ipak, tu je i jedan drugačiji primjer - str. 182.
Slijedi nekoliko primjera u skripti. Bitno je naglasiti da nakon određivanja maksimalnog toka Ford-Fulkersonovim algoritmom možemo jednostavno provjeriti je li tok zaista optimalan koristeći ideju dokaza Teorema 4.1 (kao npr. u rješenju Zadatka 4.3): Nakon završetka FF algoritma ako u S stavimo izvor te sve vrhove do kojih možemo doći putem povećanja toka onda i-p rez (S,S^c) ima kapacitet koji je jednak val f. Ako dođemo do takvog para, prema slaboj dualnosti znamo da su to minimalan i-p rez i maksimalan tok. Naravno, ako kapacitet nije jednak val f, onda je nešto pošlo po krivu u primjeni FF algoritma, odnosno, tekući f ipak nije maksimalan tok.
No to nije jedini način za dolazak do minimalnog i-p reza (ako znamo maksimalan tok) - mogli smo zapravo ići i od ponora i u S^c staviti sve vrhove iz kojih prema ponoru možemo poslati još robe. Potpuno općenito, to je zapisano u Zadatku 4.5 - pomoću njega praktično određujemo sve moguće i-p rezove. To je demonstrirano u nastavku (konačno rješenje Zadatka 4.4).
Ako ste riješili par zadataka, primijetit ćete da probleme s malim brojem bridova/vrhova nije teško riješiti. No kod velikih problema treba ipak malo precizirati algoritam, da ne bismo nepotrebno vrludali po grafu - to je načinjeno na str. 77. Bilo bi dobro neki od primjera riješiti i s ovim preciznim algoritmom.
Kao naprednija tema spomenuta je složenost FF algoritma, ali i jednostavna varijanta algoritma (Edmonds-Karpov algoritam) s polinomijalnom složenosti (za razliku od pseudopolinomijalne).
... nastavit će se ... (to je izgleda jedini način da post dobije odgovor :D )
str. 70 do 84 skripte. Nije stalo u naslov pa dodajem + primjena u problemu dodjeljivanja
Sama ideja algoritma već je iznesena u Primjeru 8 od prošlog tjedna. Teorem 4.1. kaže da ako trenutni tok nije optimalan moguće je naći put povećanja toka i pomoću njega prijeći na bolji tok. To doduše ne znači da će algoritam završiti u konačno mnogo koraka - mogli smo npr. napredovati za 1/2^n u n-toj iteraciji algoritma. Naravno, to nije moguće u mreži s cjelobrojnim kapacitetima, jer je napredak uvijek cjelobrojan ... kako već i piše u skripti ...
No ipak, tu je i jedan drugačiji primjer - str. 182.
Slijedi nekoliko primjera u skripti. Bitno je naglasiti da nakon određivanja maksimalnog toka Ford-Fulkersonovim algoritmom možemo jednostavno provjeriti je li tok zaista optimalan koristeći ideju dokaza Teorema 4.1 (kao npr. u rješenju Zadatka 4.3): Nakon završetka FF algoritma ako u S stavimo izvor te sve vrhove do kojih možemo doći putem povećanja toka onda i-p rez (S,S^c) ima kapacitet koji je jednak val f. Ako dođemo do takvog para, prema slaboj dualnosti znamo da su to minimalan i-p rez i maksimalan tok. Naravno, ako kapacitet nije jednak val f, onda je nešto pošlo po krivu u primjeni FF algoritma, odnosno, tekući f ipak nije maksimalan tok.
No to nije jedini način za dolazak do minimalnog i-p reza (ako znamo maksimalan tok) - mogli smo zapravo ići i od ponora i u S^c staviti sve vrhove iz kojih prema ponoru možemo poslati još robe. Potpuno općenito, to je zapisano u Zadatku 4.5 - pomoću njega praktično određujemo sve moguće i-p rezove. To je demonstrirano u nastavku (konačno rješenje Zadatka 4.4).
Ako ste riješili par zadataka, primijetit ćete da probleme s malim brojem bridova/vrhova nije teško riješiti. No kod velikih problema treba ipak malo precizirati algoritam, da ne bismo nepotrebno vrludali po grafu - to je načinjeno na str. 77. Bilo bi dobro neki od primjera riješiti i s ovim preciznim algoritmom.
Kao naprednija tema spomenuta je složenost FF algoritma, ali i jednostavna varijanta algoritma (Edmonds-Karpov algoritam) s polinomijalnom složenosti (za razliku od pseudopolinomijalne).
... nastavit će se ... (to je izgleda jedini način da post dobije odgovor  ) )
_________________
Marko Vrdoljak
|
|
| [Vrh] |
|
markov
Forumaš(ica)

Pridružen/a: 04. 01. 2006. (01:24:33)
Postovi: (121)16
|
 Postano: 20:23 sri, 1. 4. 2020 Naslov: Postano: 20:23 sri, 1. 4. 2020 Naslov: |
    |
|
|
Ostalo nam je povezati problem traženja maksimalnog toka s nalaskom maksimalnog sparivanja u bipartitnom grafu (str. 80-84)
Pitanje maksimalnog sparivanja (i minimalnog pokrivača) pojavilo nam se u mađarskoj metodi - u skupu svih nula u matrici želimo naći maksimalan podskup takav da nikoje dvije nisu u istom retku niti u istom stupcu. S druge strane, minimalan pokrivač je najmanji (po broju) skup redaka i/ili stupaca u kojima se nalaze sve nule - tj. skup linija (horizontalnih ili vertikalnih) koje prekrivaju sve nule u matrici.
Govorimo i o interpretaciji kroz nalazak najvećeg mogućeg broj brakova među djevojkama (retci matrice) i momcima (stupci matrice). Naravno, treba postovati simpatije, a one su upravo iskazane nulama u matrici.
Skupu svih nula u matrici pridružujemo bipartitni graf - nula na mjestu (i,j) uvodi luk kapaciteta 1 među vrhovima i i j. Za zadano sparivanje, na pripadnim lukovima stavimo tok 1, inače nula. Grafu dodajemo još izvor i ponor: izvor spajamo sa svim djevojkama lukovima kapaciteta 1, a ponor s momcima (na isti način). Daklle, sparivanju u matrici možemo jednoznačno pridružiti cjelobojni dopustivi tok na transportnoj mreži. No možemo i obratno, cjelobrojnom toku pridružujemo sparivanje tako da uočimo lukove
od djevojaka do momaka na kojima je tok jednak 1. Dakle, veza je bijektivna, a vrijednost toka je jednaka broju brakova, tako da sve što trebamo je upravo odrediti maksimalan tok. Radimo to FF-algoritmom i zapravo pratimo koju interpretaciju koraci tog algoritma imaju u paralelnom problemu sparivanja. Posebno, ako primjenimo algoritam oznacavanja i obradjivanja sa str. 77 dolazimo do algoritma za maksimalno sparivanje sa str. 83.
Pokušajte primijeniti taj algoritam na nekoliko primjera (str. 162). Zanimljivo je što kad algoritam završi možemo očitati i minimalan pokrivač - to nam je ključno za nastavak algoritma mađarske metode. Recept piše u zadnjoj rečenici na str. 83 (malo složenije - razmislite zašo je recept dobar). Točka završava s ocjenom složenosti metode - malo složenije, ali razmislite i o tome.
Ostalo nam je povezati problem traženja maksimalnog toka s nalaskom maksimalnog sparivanja u bipartitnom grafu (str. 80-84)
Pitanje maksimalnog sparivanja (i minimalnog pokrivača) pojavilo nam se u mađarskoj metodi - u skupu svih nula u matrici želimo naći maksimalan podskup takav da nikoje dvije nisu u istom retku niti u istom stupcu. S druge strane, minimalan pokrivač je najmanji (po broju) skup redaka i/ili stupaca u kojima se nalaze sve nule - tj. skup linija (horizontalnih ili vertikalnih) koje prekrivaju sve nule u matrici.
Govorimo i o interpretaciji kroz nalazak najvećeg mogućeg broj brakova među djevojkama (retci matrice) i momcima (stupci matrice). Naravno, treba postovati simpatije, a one su upravo iskazane nulama u matrici.
Skupu svih nula u matrici pridružujemo bipartitni graf - nula na mjestu (i,j) uvodi luk kapaciteta 1 među vrhovima i i j. Za zadano sparivanje, na pripadnim lukovima stavimo tok 1, inače nula. Grafu dodajemo još izvor i ponor: izvor spajamo sa svim djevojkama lukovima kapaciteta 1, a ponor s momcima (na isti način). Daklle, sparivanju u matrici možemo jednoznačno pridružiti cjelobojni dopustivi tok na transportnoj mreži. No možemo i obratno, cjelobrojnom toku pridružujemo sparivanje tako da uočimo lukove
od djevojaka do momaka na kojima je tok jednak 1. Dakle, veza je bijektivna, a vrijednost toka je jednaka broju brakova, tako da sve što trebamo je upravo odrediti maksimalan tok. Radimo to FF-algoritmom i zapravo pratimo koju interpretaciju koraci tog algoritma imaju u paralelnom problemu sparivanja. Posebno, ako primjenimo algoritam oznacavanja i obradjivanja sa str. 77 dolazimo do algoritma za maksimalno sparivanje sa str. 83.
Pokušajte primijeniti taj algoritam na nekoliko primjera (str. 162). Zanimljivo je što kad algoritam završi možemo očitati i minimalan pokrivač - to nam je ključno za nastavak algoritma mađarske metode. Recept piše u zadnjoj rečenici na str. 83 (malo složenije - razmislite zašo je recept dobar). Točka završava s ocjenom složenosti metode - malo složenije, ali razmislite i o tome.
_________________
Marko Vrdoljak
|
|
| [Vrh] |
|
markov
Forumaš(ica)

Pridružen/a: 04. 01. 2006. (01:24:33)
Postovi: (121)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
markov
Forumaš(ica)

Pridružen/a: 04. 01. 2006. (01:24:33)
Postovi: (121)16
|
 Postano: 21:27 sub, 11. 4. 2020 Naslov: Postano: 21:27 sub, 11. 4. 2020 Naslov: |
    |
|
|
Pogledat ću još imam li zadataka s uredno zapisanim rješenjima, no sumnjam. Slobodno
pitajte što vas zanima. Također, možete mi i poslati upitna rješenja pa ću pregledati ili ona manje upitna pa mogu dodati u skriptu barem samo rezultat.
Rješenje zadatka 10.17 (dio b) je u privitku. Za dio a, nakon oduzimanja najmanjeg elementa u svakom retku pa u svakom stupcu dolazimo do matrice
[table]
0 9 6 7 3 0
1 0 7 0 5 3
3 5 6 6 0 7
1 6 0 16 10 2
7 0 3 10 1 2
1 7 2 3 0 1
[/table]
Minimalan pokrivač ima 5 linija (npr. 1, 2, 4. i 5. redak i 5. stupac; nije teško uočiti sparivanje s 5 nula) pa je iduća matrica dana s
[table]
0 9 6 7 4 0
1 0 7 0 6 3
2 4 5 5 0 6
1 6 0 16 11 2
7 0 3 10 2 2
0 6 1 2 0 0
[/table]
Sad postoji potpuno sparivanje. Gledajući prvo redom po stupcima, vidimo da za potpuno sparivanje moramo uzeti nule na mjestu (4,3), (2,4).
Također, gledajući po retcima, samo je jedna nula u 3, 4. i 5. retku, pa dobivamo još dvije nule (3,5) i (5,2) (za 4. redak smo već uzeli (4,3)). Dakle, riješili smo sve osim prvog i zadnjg retka te prvog i zadnjeg stupca - na toj podmatrici imamo sve četiri nule, što nam daje dva moguća rješenja: (1,1) i (6,6) ili (1,6) i (6,1).
Pogledat ću još imam li zadataka s uredno zapisanim rješenjima, no sumnjam. Slobodno
pitajte što vas zanima. Također, možete mi i poslati upitna rješenja pa ću pregledati ili ona manje upitna pa mogu dodati u skriptu barem samo rezultat.
Rješenje zadatka 10.17 (dio b) je u privitku. Za dio a, nakon oduzimanja najmanjeg elementa u svakom retku pa u svakom stupcu dolazimo do matrice
| 0 | 9 | 6 | 7 | 3 | 0 | | 1 | 0 | 7 | 0 | 5 | 3 | | 3 | 5 | 6 | 6 | 0 | 7 | | 1 | 6 | 0 | 16 | 10 | 2 | | 7 | 0 | 3 | 10 | 1 | 2 | | 1 | 7 | 2 | 3 | 0 | 1 |
Minimalan pokrivač ima 5 linija (npr. 1, 2, 4. i 5. redak i 5. stupac; nije teško uočiti sparivanje s 5 nula) pa je iduća matrica dana s
| 0 | 9 | 6 | 7 | 4 | 0 | | 1 | 0 | 7 | 0 | 6 | 3 | | 2 | 4 | 5 | 5 | 0 | 6 | | 1 | 6 | 0 | 16 | 11 | 2 | | 7 | 0 | 3 | 10 | 2 | 2 | | 0 | 6 | 1 | 2 | 0 | 0 |
Sad postoji potpuno sparivanje. Gledajući prvo redom po stupcima, vidimo da za potpuno sparivanje moramo uzeti nule na mjestu (4,3), (2,4).
Također, gledajući po retcima, samo je jedna nula u 3, 4. i 5. retku, pa dobivamo još dvije nule (3,5) i (5,2) (za 4. redak smo već uzeli (4,3)). Dakle, riješili smo sve osim prvog i zadnjg retka te prvog i zadnjeg stupca - na toj podmatrici imamo sve četiri nule, što nam daje dva moguća rješenja: (1,1) i (6,6) ili (1,6) i (6,1).
_________________
Marko Vrdoljak
| Description: |
|

Download |
| Filename: |
zadatak10.17.pdf |
| Filesize: |
105.81 KB |
| Downloaded: |
225 Time(s) |
|
|
| [Vrh] |
|
markov
Forumaš(ica)

Pridružen/a: 04. 01. 2006. (01:24:33)
Postovi: (121)16
|
 Postano: 18:28 uto, 14. 4. 2020 Naslov: Postano: 18:28 uto, 14. 4. 2020 Naslov: |
    |
|
|
Rezultati par zadataka iz skripte:
[b]10.5. [/b] Rješenje je jedinstveno: [latex] x_{12}=5, x_{14}=10, x_{22}=10, x_{23}=15, x_{31}=5, x_{34}=5.[/latex]
[b]10.7. [/b] Rješenje je jedinstveno: [latex] x_{12}=3, x_{14}=6, x_{22}=6, x_{23}=9, x_{31}=3, x_{34}=3.[/latex]
[b]10.18. [/b] Imamo četiri optimalna rasporeda: a) A1, B2, C4, D3 b) A1, B3, C2, D4 c) A3, B1, C2, D4 d) A3, B2, C1, D4.
Rezultati par zadataka iz skripte:
10.5. Rješenje je jedinstveno: 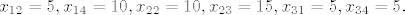
10.7. Rješenje je jedinstveno: 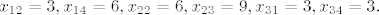
10.18. Imamo četiri optimalna rasporeda: a) A1, B2, C4, D3 b) A1, B3, C2, D4 c) A3, B1, C2, D4 d) A3, B2, C1, D4.
_________________
Marko Vrdoljak
|
|
| [Vrh] |
|
|



