| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 19:34 sub, 2. 10. 2004 Naslov: Re: Ekstr. svojstva spektra sim. matrice, tm1.4 Postano: 19:34 sub, 2. 10. 2004 Naslov: Re: Ekstr. svojstva spektra sim. matrice, tm1.4 |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"]Neka je C simetricna matrica, tada vrijedi:
[list]i) sve su svojstvene vrijednosti od C realne
ii) ako definiramo:
[latex]\displaystyle m:= \min_{y \in S^{n-1}} y^\tau C Y [/latex]
tada je m<= od svake svojstvene vrijednosti operatora(matrice) C
iii) m je sv. vrijednost od C[/list:u]
Dokaz tocke i) je iz nedefinirane knjige Svetozara Kurepe :shock: help :shock:[/quote]
KDVP&P nipošto nije nedefinirana knjiga :!:
No dobro... ako je matrica simetrična, to ujedno znači da je realna (simetričnost je definirana samo za realne matrice), i da je C^*=C (* je hermitsko adjungiranje).
Pretpostavimo lam@sigma(C) , odnosno Cx=lamx . To znači
(x|Cx)=(C^* x|x)=(Cx|x)
(x|lamx)=(lamx|x)
lam(^~)(x|x)=lam(x|x)
lam=lam^~ V (x|x)=0
Jer je x svojstveni vektor, x nije nulvektor, pa je (x|x)>0 . Dakle mora biti lam=lam^~ , odnosno lam@|R .
[quote]a tocke ii) :
[quote="Prof. Caklovic u skripti"][latex]ii)$ Odaberimo svojstven par $\lambda,y,|y\|=1$. Tada je$...[/latex][/quote]
:shock: jel netko zna sto je pisac htio reci i sto bi to bio svojstven "par" :( ?[/quote]
Jednostavno, neka je lambda bilo koja svojstvena vrijednost. To znači da ima neki svojstveni vektor y1 (koji nije nulvektor), pa s y označimo normirani y1/|y1| . y će također biti svojstveni vektor za lambda .
| ZELENIZUBNAPLANETIDOSADE (napisa): | Neka je C simetricna matrica, tada vrijedi:
i) sve su svojstvene vrijednosti od C realne
ii) ako definiramo:
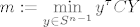
tada je m⇐ od svake svojstvene vrijednosti operatora(matrice) C
iii) m je sv. vrijednost od C
Dokaz tocke i) je iz nedefinirane knjige Svetozara Kurepe  help help  |
KDVP&P nipošto nije nedefinirana knjiga 
No dobro... ako je matrica simetrična, to ujedno znači da je realna (simetričnost je definirana samo za realne matrice), i da je C^*=C (* je hermitsko adjungiranje).
Pretpostavimo lam@sigma(C) , odnosno Cx=lamx . To znači
(x|Cx)=(C^* x|x)=(Cx|x)
(x|lamx)=(lamx|x)
lam(^~)(x|x)=lam(x|x)
lam=lam^~ V (x|x)=0
Jer je x svojstveni vektor, x nije nulvektor, pa je (x|x)>0 . Dakle mora biti lam=lam^~ , odnosno lam@|R .
| Citat: | a tocke ii) :
| Prof. Caklovic u skripti (napisa): |  |
 jel netko zna sto je pisac htio reci i sto bi to bio svojstven "par" jel netko zna sto je pisac htio reci i sto bi to bio svojstven "par"  ? ? |
Jednostavno, neka je lambda bilo koja svojstvena vrijednost. To znači da ima neki svojstveni vektor y1 (koji nije nulvektor), pa s y označimo normirani y1/|y1| . y će također biti svojstveni vektor za lambda .
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 12:55 ned, 3. 10. 2004 Naslov: Postano: 12:55 ned, 3. 10. 2004 Naslov: |
    |
|
|
[quote="Anonymous"]To je iz drugog dijela vekyjevog odgovora, dakle za simetrični operator prostor je direktna suma njegove slike i jezgre. Znači, ne samo da postoji potprostor izomorfan slici koji je direktni komplement jezgre, nego je taj potprostor upravo sama slika.[/quote]
A-ha :) hvala :)
| Anonymous (napisa): | | To je iz drugog dijela vekyjevog odgovora, dakle za simetrični operator prostor je direktna suma njegove slike i jezgre. Znači, ne samo da postoji potprostor izomorfan slici koji je direktni komplement jezgre, nego je taj potprostor upravo sama slika. |
A-ha  hvala hvala 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
|




