| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 18:04 ned, 5. 12. 2004 Naslov: Propozicija o ''uniji slika i presjeku slika'' Postano: 18:04 ned, 5. 12. 2004 Naslov: Propozicija o ''uniji slika i presjeku slika'' |
    |
|
|
[color=green]Propozicija(gradivo:funkcije):
Pretpostavke: f:A->B , X,Y C= A
Doprinos:
(i)f(XuY)=f(X)uf(Y)
(ii)f(XnY) C= f(X)nf(Y)[/color]
(zar u tvrdnji (ii) ne stoji uvjet XnY!=0 ?
Uvjet je nenužan ako smo se dogovorili da je slika praznog skupa prazan skup,a to je sasvim moguće jer:
prije no što se definira skup oznake f(Ž) zahtjeva se da je Ž C= prirodne domene ,a prazan skup je podskup svakoga skupa pa specijalno i prirodne domene što će omogućiti praznom skupu da se ''progura'' u definiciju slike ?
Laganini sam zbunjen... )
DOKAZI:
Tvrdnja: f(XuY)=f(X)uf(Y)
( Tvrdnja=>Tvrdnja1:f(XuY) C= f(X)uf(Y) i Tvrdnja2:f(X)uf(Y) C= f(XuY) )
DOKAZ:
Proizvoljni a@f(XuY) ,slika nekog skupa po funkciji nikad nije prazan skup pa sadrži barem jedan element(konstantna funkcija)
Definicija slike<=>postoji neki b@XuY sa svojstvom f(b)=a
Definicija unije<=>b@X ili b@Y , f(b)=a
Definicija slike<=>f(b)@f(X) ili f(b)@f(X) , f(b)=a
Definicija unije<=>f(b)=a@f(X)uf(Y) CUBE;)
Pitanja:
1.Jesam li morao od ''kreiranja'' pretpostavke f(b)=a ''vući ju'' kroz preostale ekvivalencije ili sam jednostavno mogao u početku(kada sam napisao ''Proizvoljni a@f(XuY)'') staviti a:=f(b) pa bi ona bila uključena u svim ekvivalencijama ?
2.Što da sam kod ekvivalencije b@X ili b@Y , f(b)=a krenuo ovako dalje:
I)b@X , f(b)=a
II)b@Y , f(b)=a
Kako bih tada uspio dokazati tvrdnju1 ?
Tvrdnja:f(XnY) C= f(X)nf(Y)
DOKAZ:
Ok,potrebno je dokazati jednu inkluziju(slijeva nadesno) i to je to.
Kako bi dokazao da je tvrdnja(uz pretpostavke teorema dakako) zadana izvan teorema(kao recimo-zadatak) i gdje između skupova f(XnY) i f(X)nf(Y) nema nikakve relacije(time mislim na znak 'C=' ),te gdje je rečeno:'Što stoji između skupova,jednakost ili koja inkluzija ?' ?
Ovako:
DOKAZ:
Vjerujem da je dovoljno dokazati 'C=' i dati kontraprimjer što pobija jednakost f(XnY)=f(X)nf(Y),pa evo:
a@f(XnY) ,slika nekog skupa(podskupa domene) je uvijek neprazan skup pa 'a' postoji.
Def.slike=>postoji b@XnY sa svojstvom f(b)=a
Def.presjeka=>b@X i b@Y , f(b)=a
Def.slike=>f(b)@f(X) i f(b)@f(Y) ,f(b)=a
Def.presjeka=>f(b)@f(X)nf(Y) CUBE;)
Kontraprimjer što pobija jednakost f(XnY)=f(X)nf(Y) :
f:IR->IR , f(x)=x^2
X=<-oo,0]
Y=[0,+oo>
XnY={0}=>f(XnY)={0}
f(X)=[0,+oo>
f(Y)=[0,+oo>
f(X)nf(Y)=[0,+oo>
zaključak:{0}!={x:x@IR^+} ,odnosno f(XnY) C= f(X)nf(Y)
Ukoliko ne bi koristio kontraprimjer što pobija jednakost,morao bi opovrgnuti inkluziju:f(X)nf(Y) C= f(XnY) ,kako ovo srušiti ?
Propozicija(gradivo:funkcije):
Pretpostavke: f:A→B , X,Y C= A
Doprinos:
(i)f(XuY)=f(X)uf(Y)
(ii)f(XnY) C= f(X)nf(Y)
(zar u tvrdnji (ii) ne stoji uvjet XnY!=0 ?
Uvjet je nenužan ako smo se dogovorili da je slika praznog skupa prazan skup,a to je sasvim moguće jer:
prije no što se definira skup oznake f(Ž) zahtjeva se da je Ž C= prirodne domene ,a prazan skup je podskup svakoga skupa pa specijalno i prirodne domene što će omogućiti praznom skupu da se ''progura'' u definiciju slike ?
Laganini sam zbunjen... )
DOKAZI:
Tvrdnja: f(XuY)=f(X)uf(Y)
( Tvrdnja⇒Tvrdnja1:f(XuY) C= f(X)uf(Y) i Tvrdnja2:f(X)uf(Y) C= f(XuY) )
DOKAZ:
Proizvoljni a@f(XuY) ,slika nekog skupa po funkciji nikad nije prazan skup pa sadrži barem jedan element(konstantna funkcija)
Definicija slike⇔postoji neki b@XuY sa svojstvom f(b)=a
Definicija unije⇔b@X ili b@Y , f(b)=a
Definicija slike⇔f(b)@f(X) ili f(b)@f(X) , f(b)=a
Definicija unije⇔f(b)=a@f(X)uf(Y) CUBE;)
Pitanja:
1.Jesam li morao od ''kreiranja'' pretpostavke f(b)=a ''vući ju'' kroz preostale ekvivalencije ili sam jednostavno mogao u početku(kada sam napisao ''Proizvoljni a@f(XuY)'') staviti a:=f(b) pa bi ona bila uključena u svim ekvivalencijama ?
2.Što da sam kod ekvivalencije b@X ili b@Y , f(b)=a krenuo ovako dalje:
I)b@X , f(b)=a
II)b@Y , f(b)=a
Kako bih tada uspio dokazati tvrdnju1 ?
Tvrdnja:f(XnY) C= f(X)nf(Y)
DOKAZ:
Ok,potrebno je dokazati jednu inkluziju(slijeva nadesno) i to je to.
Kako bi dokazao da je tvrdnja(uz pretpostavke teorema dakako) zadana izvan teorema(kao recimo-zadatak) i gdje između skupova f(XnY) i f(X)nf(Y) nema nikakve relacije(time mislim na znak 'C=' ),te gdje je rečeno:'Što stoji između skupova,jednakost ili koja inkluzija ?' ?
Ovako:
DOKAZ:
Vjerujem da je dovoljno dokazati 'C=' i dati kontraprimjer što pobija jednakost f(XnY)=f(X)nf(Y),pa evo:
a@f(XnY) ,slika nekog skupa(podskupa domene) je uvijek neprazan skup pa 'a' postoji.
Def.slike⇒postoji b@XnY sa svojstvom f(b)=a
Def.presjeka⇒b@X i b@Y , f(b)=a
Def.slike⇒f(b)@f(X) i f(b)@f(Y) ,f(b)=a
Def.presjeka⇒f(b)@f(X)nf(Y) CUBE;)
Kontraprimjer što pobija jednakost f(XnY)=f(X)nf(Y) :
f:IR→IR , f(x)=x^2
X=←oo,0]
Y=[0,+oo>
XnY={0}⇒f(XnY)={0}
f(X)=[0,+oo>
f(Y)=[0,+oo>
f(X)nf(Y)=[0,+oo>
zaključak:{0}!={x @IR^+} ,odnosno f(XnY) C= f(X)nf(Y) @IR^+} ,odnosno f(XnY) C= f(X)nf(Y)
Ukoliko ne bi koristio kontraprimjer što pobija jednakost,morao bi opovrgnuti inkluziju:f(X)nf(Y) C= f(XnY) ,kako ovo srušiti ?
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 19:59 ned, 5. 12. 2004 Naslov: Re: Propozicija o ''uniji slika i presjeku slika'' Postano: 19:59 ned, 5. 12. 2004 Naslov: Re: Propozicija o ''uniji slika i presjeku slika'' |
    |
|
|
[quote="Vincent Van Ear"][color=green]Propozicija(gradivo:funkcije):
Pretpostavke: f:A->B , X,Y C= A
Doprinos:
(i)f(XuY)=f(X)uf(Y)
(ii)f(XnY) C= f(X)nf(Y)[/color]
(zar u tvrdnji (ii) ne stoji uvjet XnY!=0 ?
Uvjet je nenužan ako smo se dogovorili da je slika praznog skupa prazan skup,a to je sasvim moguće jer:
prije no što se definira skup oznake f(Ž) zahtjeva se da je Ž C= prirodne domene ,a prazan skup je podskup svakoga skupa pa specijalno i prirodne domene što će omogućiti praznom skupu da se ''progura'' u definiciju slike ?
Laganini sam zbunjen... )[/quote]
Ne vidim zašto si zbunjen. Sve što si rekao je potpuno točno. Daj prestani već jednom tretirati prazan skup kao nešto užasno specijalno, i prihvati ga kao normalni math-objekt. :-)
Da, f^>(0)=0 (slika praznog skupa je prazan skup), i ti to jako dobro znaš. Slijedi iz definicije: slika praznog skupa je skup svih f(x) , gdje je x@0 . Budući da je x@0 uvijek lažno, takvih x-eva nema, pa nema ni njihovih f-ova, odnosno skup svih takvih f-ova je prazan. 8)
[quote]Proizvoljni a@f(XuY) ,slika nekog skupa po funkciji nikad nije prazan skup pa sadrži barem jedan element(konstantna funkcija)[/quote]
Opet ti.
Što će ti ovo? Da bi dokazao da je jedan skup podskup drugoga, nikad ti dosad nije trebala pretpostavka da je taj skup neprazan. Zašto je sad uzimaš? Tim više što je kriva. Gore piše, slika praznog skupa je prazna.
[quote]Definicija slike<=>postoji neki b@XuY sa svojstvom f(b)=a[/quote]
Bilo bi bolje (bar u donjim redovima, ako već ne i ovdje) ne pisati ekvivalencije u ovakvom obliku. Naime, desna strana svake ekvivalencije jest posljedica lijeve (dok je obrat puno čudnije shvatiti tako), ali i prethodnog retka. Možda je bolje staviti "definicija slike" u komentar, kao
a@f^>(XuY) <=>(*definicija slike*) (Eb@XuY)(f(b)=a) <=>(*definicija unije*) ... i tako dalje.
[quote]
1.Jesam li morao od ''kreiranja'' pretpostavke f(b)=a ''vući ju'' kroz preostale ekvivalencije[/quote]
Nisi. Ako naznačiš da se _b_ definira tako da f(b) bude a . (nastavak)
[quote] ili sam jednostavno mogao u početku(kada sam napisao ''Proizvoljni a@f(XuY)'') staviti a:=f(b) pa bi ona bila uključena u svim ekvivalencijama ?[/quote]
[nastavak] no to _ne_ činiš tako da kažeš a:=f(b) . To bi značilo da si (re)definirao a , što naravno ne želiš. Eventualno a=:f(b) (ovdje može proći, jer je sasvim jasno da ne definiraš f : ), ili preciznije
b: f(b)=a .
[quote]2.Što da sam kod ekvivalencije b@X ili b@Y , f(b)=a krenuo ovako dalje:
I)b@X , f(b)=a
II)b@Y , f(b)=a
Kako bih tada uspio dokazati tvrdnju1 ?[/quote]
I) b@X & f(b)=a => a = f(b) @ f^>(X) C= f^>(X) u f^>(Y) .
II) sâm. ;-)
[quote]Tvrdnja:f(XnY) C= f(X)nf(Y)
DOKAZ:
Ok,potrebno je dokazati jednu inkluziju(slijeva nadesno) i to je to.[/quote]
Ne da ti se pisati? :-P
[quote]Kako bi dokazao da je tvrdnja(uz pretpostavke teorema dakako) zadana izvan teorema(kao recimo-zadatak) i gdje između skupova f(XnY) i f(X)nf(Y) nema nikakve relacije(time mislim na znak 'C=' ),te gdje je rečeno:'Što stoji između skupova,jednakost ili koja inkluzija ?' ?
Ovako:
DOKAZ:
Vjerujem da je dovoljno dokazati 'C=' i dati kontraprimjer što pobija jednakost f(XnY)=f(X)nf(Y),pa evo:[/quote]
Sve ok, ako imaš neku osnovu na koju to vjeruješ. :-)
(Vennovi dijagrami ovdje ne pomažu ;-p )
[quote]a@f(XnY) ,slika nekog skupa(podskupa domene) je uvijek neprazan skup pa 'a' postoji.[/quote]
Argh. Netočno.
Da raščistimo to već jednom. Kad ti dokazuješ da je S podskup od T , ti _pretpostaviš_ x@S i iz toga nastojiš zaključiti x@T . Nigdje ti ne treba da S != 0 , odnosno da je tvoja pretpostavka stvarno ispunjiva. Štoviše, kad je univerzalno lažna ( S=0 ), tvoj posao je tim laši, jer implikacija tim trivijalnije vrijedi.
[quote]Def.slike=>postoji b@XnY sa svojstvom f(b)=a[/quote]
Vidim da si odustao od "definicija...<=>"-stila i prešao na "=>"-stil. Bolje, ali još uvijek nedovoljno dobro. Definicije su ovdje pomoćne tvrdnje koje koristiš da bi izgradio lanac implikacija, ne same karike. One su cement, ne cigle. ;-)
[quote]f:IR->IR , f(x)=x^2
X=<-oo,0]
Y=[0,+oo>
XnY={0}=>f(XnY)={0}
f(X)=[0,+oo>
f(Y)=[0,+oo>
f(X)nf(Y)=[0,+oo>
zaključak:{0}!={x: x@IR^+} ,odnosno f(XnY) C= f(X)nf(Y)[/quote]
Preciznije, "C" (_pravi_ podskup), općenito. Da je podskup si dokazao već gore.
[quote]Ukoliko ne bi koristio kontraprimjer što pobija jednakost,morao bi opovrgnuti inkluziju:f(X)nf(Y) C= f(XnY) ,kako ovo srušiti ?[/quote]
Istim kontraprimjerom. :-) (Naravno, budući da se za skupove jednakost sastoji od dvije inkluzije, a jednu si dokazao da vrijedi, zapravo i ne možeš opovrgnuti išta drugo. : )
Imaš f^>(XnY)={0} , dakle 1(@!)f^>(XnY) .
S druge strane, f^>(X)nf^>(Y)=|R^+_0 , dakle 1@f^>(X)nf^>(Y) .
Dakle drugi nije podskup od prvog. kved.
HTH,
| Vincent Van Ear (napisa): | Propozicija(gradivo:funkcije):
Pretpostavke: f:A→B , X,Y C= A
Doprinos:
(i)f(XuY)=f(X)uf(Y)
(ii)f(XnY) C= f(X)nf(Y)
(zar u tvrdnji (ii) ne stoji uvjet XnY!=0 ?
Uvjet je nenužan ako smo se dogovorili da je slika praznog skupa prazan skup,a to je sasvim moguće jer:
prije no što se definira skup oznake f(Ž) zahtjeva se da je Ž C= prirodne domene ,a prazan skup je podskup svakoga skupa pa specijalno i prirodne domene što će omogućiti praznom skupu da se ''progura'' u definiciju slike ?
Laganini sam zbunjen... ) |
Ne vidim zašto si zbunjen. Sve što si rekao je potpuno točno. Daj prestani već jednom tretirati prazan skup kao nešto užasno specijalno, i prihvati ga kao normalni math-objekt. 
Da, f^>(0)=0 (slika praznog skupa je prazan skup), i ti to jako dobro znaš. Slijedi iz definicije: slika praznog skupa je skup svih f(x) , gdje je x@0 . Budući da je x@0 uvijek lažno, takvih x-eva nema, pa nema ni njihovih f-ova, odnosno skup svih takvih f-ova je prazan. 
| Citat: | | Proizvoljni a@f(XuY) ,slika nekog skupa po funkciji nikad nije prazan skup pa sadrži barem jedan element(konstantna funkcija) |
Opet ti.
Što će ti ovo? Da bi dokazao da je jedan skup podskup drugoga, nikad ti dosad nije trebala pretpostavka da je taj skup neprazan. Zašto je sad uzimaš? Tim više što je kriva. Gore piše, slika praznog skupa je prazna.
| Citat: | | Definicija slike⇔postoji neki b@XuY sa svojstvom f(b)=a |
Bilo bi bolje (bar u donjim redovima, ako već ne i ovdje) ne pisati ekvivalencije u ovakvom obliku. Naime, desna strana svake ekvivalencije jest posljedica lijeve (dok je obrat puno čudnije shvatiti tako), ali i prethodnog retka. Možda je bolje staviti "definicija slike" u komentar, kao
a@f^>(XuY) ⇔(*definicija slike*) (Eb@XuY)(f(b)=a) ⇔(*definicija unije*) ... i tako dalje.
| Citat: |
1.Jesam li morao od ''kreiranja'' pretpostavke f(b)=a ''vući ju'' kroz preostale ekvivalencije |
Nisi. Ako naznačiš da se _b_ definira tako da f(b) bude a . (nastavak)
| Citat: | | ili sam jednostavno mogao u početku(kada sam napisao ''Proizvoljni a@f(XuY)'') staviti a:=f(b) pa bi ona bila uključena u svim ekvivalencijama ? |
[nastavak] no to _ne_ činiš tako da kažeš a:=f(b) . To bi značilo da si (re)definirao a , što naravno ne želiš. Eventualno a=:f(b) (ovdje može proći, jer je sasvim jasno da ne definiraš f : ), ili preciznije
b: f(b)=a .
| Citat: | 2.Što da sam kod ekvivalencije b@X ili b@Y , f(b)=a krenuo ovako dalje:
I)b@X , f(b)=a
II)b@Y , f(b)=a
Kako bih tada uspio dokazati tvrdnju1 ? |
I) b@X & f(b)=a ⇒ a = f(b) @ f^>(X) C= f^>(X) u f^>(Y) .
II) sâm. 
| Citat: | Tvrdnja:f(XnY) C= f(X)nf(Y)
DOKAZ:
Ok,potrebno je dokazati jednu inkluziju(slijeva nadesno) i to je to. |
Ne da ti se pisati? 
| Citat: | Kako bi dokazao da je tvrdnja(uz pretpostavke teorema dakako) zadana izvan teorema(kao recimo-zadatak) i gdje između skupova f(XnY) i f(X)nf(Y) nema nikakve relacije(time mislim na znak 'C=' ),te gdje je rečeno:'Što stoji između skupova,jednakost ili koja inkluzija ?' ?
Ovako:
DOKAZ:
Vjerujem da je dovoljno dokazati 'C=' i dati kontraprimjer što pobija jednakost f(XnY)=f(X)nf(Y),pa evo: |
Sve ok, ako imaš neku osnovu na koju to vjeruješ. 
(Vennovi dijagrami ovdje ne pomažu ;-p )
| Citat: | | a@f(XnY) ,slika nekog skupa(podskupa domene) je uvijek neprazan skup pa 'a' postoji. |
Argh. Netočno.
Da raščistimo to već jednom. Kad ti dokazuješ da je S podskup od T , ti _pretpostaviš_ x@S i iz toga nastojiš zaključiti x@T . Nigdje ti ne treba da S != 0 , odnosno da je tvoja pretpostavka stvarno ispunjiva. Štoviše, kad je univerzalno lažna ( S=0 ), tvoj posao je tim laši, jer implikacija tim trivijalnije vrijedi.
| Citat: | | Def.slike⇒postoji b@XnY sa svojstvom f(b)=a |
Vidim da si odustao od "definicija...⇔"-stila i prešao na "⇒"-stil. Bolje, ali još uvijek nedovoljno dobro. Definicije su ovdje pomoćne tvrdnje koje koristiš da bi izgradio lanac implikacija, ne same karike. One su cement, ne cigle. 
| Citat: | f:IR→IR , f(x)=x^2
X=←oo,0]
Y=[0,+oo>
XnY={0}⇒f(XnY)={0}
f(X)=[0,+oo>
f(Y)=[0,+oo>
f(X)nf(Y)=[0,+oo>
zaključak:{0}!={x: x@IR^+} ,odnosno f(XnY) C= f(X)nf(Y) |
Preciznije, "C" (_pravi_ podskup), općenito. Da je podskup si dokazao već gore.
| Citat: | | Ukoliko ne bi koristio kontraprimjer što pobija jednakost,morao bi opovrgnuti inkluziju:f(X)nf(Y) C= f(XnY) ,kako ovo srušiti ? |
Istim kontraprimjerom.  (Naravno, budući da se za skupove jednakost sastoji od dvije inkluzije, a jednu si dokazao da vrijedi, zapravo i ne možeš opovrgnuti išta drugo. : ) (Naravno, budući da se za skupove jednakost sastoji od dvije inkluzije, a jednu si dokazao da vrijedi, zapravo i ne možeš opovrgnuti išta drugo. : )
Imaš f^>(XnY)={0} , dakle 1(@!)f^>(XnY) .
S druge strane, f^>(X)nf^>(Y)=|R^+_0 , dakle 1@f^>(X)nf^>(Y) .
Dakle drugi nije podskup od prvog. kved.
HTH,
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 21:54 ned, 5. 12. 2004 Naslov: Postano: 21:54 ned, 5. 12. 2004 Naslov: |
    |
|
|
[quote] Daj prestani već jednom tretirati prazan skup kao nešto užasno specijalno, i prihvati ga kao normalni math-objekt. [/quote]
Tek kad se on i ja u potpunosti sprijateljimo :mrgreen: ,do tada smo još uvijek u relaciji kakvu su imali ''indijanci i (nikad viđeni)bijeli bizoni'':mrgreen:,pa vidiš i sam kako me taj skup sramoti :shocked!: :o) .
[quote]f^>(0)=0 (slika praznog skupa je prazan skup),[/quote]
Ima li imalo sugestivnosti u oznaci slike ili ju ja jednostavno ne razaznajem ? :o)
[quote][quote]Citat:
Proizvoljni a@f(XuY) ,slika nekog skupa po funkciji nikad nije prazan skup pa sadrži barem jedan element(konstantna funkcija) [/quote]
Opet ti.
Što će ti ovo?[/quote]
Htjede su uvjeriti da sam doista uzeo nešto ''opipljivo'' iz skupa f(XuY)... :-k ...wrong,neznam kako mi napamet nije palo da X i Y mogu biti prazni...
[quote] Bilo bi bolje (bar u donjim redovima, ako već ne i ovdje) ne pisati ekvivalencije u ovakvom obliku. Naime, desna strana svake ekvivalencije jest posljedica lijeve (dok je obrat puno čudnije shvatiti tako), ali i prethodnog retka. Možda je bolje staviti "definicija slike" u komentar, kao
a@f^>(XuY) <=>(*definicija slike*) (Eb@XuY)(f(b)=a) <=>(*definicija unije*) ... i tako dalje.[/quote]
Ok.
[quote] [nastavak] no to _ne_ činiš tako da kažeš a:=f(b) . To bi značilo da si (re)definirao a , što naravno ne želiš. Eventualno a=:f(b) (ovdje može proći, jer je sasvim jasno da ne definiraš f : ), ili preciznije
b: f(b)=a[/quote]
Ok.
[quote][quote] Citat:
2.Što da sam kod ekvivalencije b@X ili b@Y , f(b)=a krenuo ovako dalje:
I)b@X , f(b)=a
II)b@Y , f(b)=a
Kako bih tada uspio dokazati tvrdnju1 ? [/quote]
I) b@X & f(b)=a => a = f(b) @ f^>(X) C= f^>(X) u f^>(Y) .
II) sâm. [/quote]
O Bože,što sam plitak...
Pretpostavljam da ovdje nije bilo nužno(za razliku od slike praznog skupa,gdje je ona morala biti naznačena drukčije od f(0) što bi upućivalo na vrijednost funkcije u točki 0) pisati sliku kao f^>(X) već jednostavnije f(X) s obzirom da smo se dogovorili da ćemo skupove označavati velikim slovima engleskog alfabeta.
II)b@Y & f(b)=a=> a=f(b)@f^>(Y) C= f^>(Y) u f^>(X) (*unija skupova je komutativna*)
[quote] Ne da ti se pisati? [/quote]
Ubuduće budem.
Mislio sam da se tebi neće dati čitati ako to napišem tu,pa opet naniže. :-P
[quote] (Vennovi dijagrami ovdje ne pomažu ;-p )[/quote]
A nekaj sa slikama bumo smislili...#-o
[quote][quote] slika nekog skupa(podskupa domene) je uvijek neprazan skup pa 'a' postoji. [/quote]
Argh. Netočno.
Da raščistimo to već jednom. Kad ti dokazuješ da je S podskup od T , ti _pretpostaviš_ x@S i iz toga nastojiš zaključiti x@T . Nigdje ti ne treba da S != 0 , odnosno da je tvoja pretpostavka stvarno ispunjiva. Štoviše, kad je univerzalno lažna ( S=0 ), tvoj posao je tim laši, jer implikacija tim trivijalnije vrijedi.[/quote]
E to mi je trebalo,dakle ja PRETPOSTAVIM da imam element u skupu S,a zašto to nije pogrešno,jer(kako kažeš) laž povlači bilo što.Oj logiko,nelogična li si. :mrgreen:
Dragocjeno.:bow:
[quote][quote] Citat:
Def.slike=>postoji b@XnY sa svojstvom f(b)=a[/quote]
Vidim da si odustao od "definicija...<=>"-stila i prešao na "=>"-stil. Bolje, ali još uvijek nedovoljno dobro. Definicije su ovdje pomoćne tvrdnje koje koristiš da bi izgradio lanac implikacija, ne same karike. One su cement, ne cigle. [/quote]
Ok,od sada sve pišim u liniji.
Uglavnom,pisao sam ti to jedno ispod drugog radi preglednosti,svaki izraz 'def.nešto' se nadovezivao na prethodnu konkluziju,ma dobro,da ne kompliciram,ako smo precizni ko neurokirurgija onda i ostanimo takvi...da pacijenti dulje požive:-s :kuckkuck:
[quote][quote] Citat:
Ukoliko ne bi koristio kontraprimjer što pobija jednakost,morao bi opovrgnuti inkluziju:f(X)nf(Y) C= f(XnY) ,kako ovo srušiti ? [/quote]
Istim kontraprimjerom. (Naravno, budući da se za skupove jednakost sastoji od dvije inkluzije, a jednu si dokazao da vrijedi, zapravo i ne možeš opovrgnuti išta drugo. : )[/quote]
Dakle nemoguće je ''simbolički''(općim zapisom) srušiti gornju inkluziju,raspisivanjem doći do kontradikcije ? :-k
| Citat: | | Daj prestani već jednom tretirati prazan skup kao nešto užasno specijalno, i prihvati ga kao normalni math-objekt. |
Tek kad se on i ja u potpunosti sprijateljimo  ,do tada smo još uvijek u relaciji kakvu su imali ''indijanci i (nikad viđeni)bijeli bizoni'' ,do tada smo još uvijek u relaciji kakvu su imali ''indijanci i (nikad viđeni)bijeli bizoni'' ,pa vidiš i sam kako me taj skup sramoti ,pa vidiš i sam kako me taj skup sramoti   . .
| Citat: | | f^>(0)=0 (slika praznog skupa je prazan skup), |
Ima li imalo sugestivnosti u oznaci slike ili ju ja jednostavno ne razaznajem ? 
| Citat: | | Citat: | Citat:
Proizvoljni a@f(XuY) ,slika nekog skupa po funkciji nikad nije prazan skup pa sadrži barem jedan element(konstantna funkcija) |
Opet ti.
Što će ti ovo? |
Htjede su uvjeriti da sam doista uzeo nešto ''opipljivo'' iz skupa f(XuY)...  ...wrong,neznam kako mi napamet nije palo da X i Y mogu biti prazni... ...wrong,neznam kako mi napamet nije palo da X i Y mogu biti prazni...
| Citat: | Bilo bi bolje (bar u donjim redovima, ako već ne i ovdje) ne pisati ekvivalencije u ovakvom obliku. Naime, desna strana svake ekvivalencije jest posljedica lijeve (dok je obrat puno čudnije shvatiti tako), ali i prethodnog retka. Možda je bolje staviti "definicija slike" u komentar, kao
a@f^>(XuY) ⇔(*definicija slike*) (Eb@XuY)(f(b)=a) ⇔(*definicija unije*) ... i tako dalje. |
Ok.
| Citat: | [nastavak] no to _ne_ činiš tako da kažeš a:=f(b) . To bi značilo da si (re)definirao a , što naravno ne želiš. Eventualno a=:f(b) (ovdje može proći, jer je sasvim jasno da ne definiraš f : ), ili preciznije
b: f(b)=a |
Ok.
| Citat: | | Citat: | Citat:
2.Što da sam kod ekvivalencije b@X ili b@Y , f(b)=a krenuo ovako dalje:
I)b@X , f(b)=a
II)b@Y , f(b)=a
Kako bih tada uspio dokazati tvrdnju1 ? |
I) b@X & f(b)=a ⇒ a = f(b) @ f^>(X) C= f^>(X) u f^>(Y) .
II) sâm. |
O Bože,što sam plitak...
Pretpostavljam da ovdje nije bilo nužno(za razliku od slike praznog skupa,gdje je ona morala biti naznačena drukčije od f(0) što bi upućivalo na vrijednost funkcije u točki 0) pisati sliku kao f^>(X) već jednostavnije f(X) s obzirom da smo se dogovorili da ćemo skupove označavati velikim slovima engleskog alfabeta.
II)b@Y & f(b)=a⇒ a=f(b)@f^>(Y) C= f^>(Y) u f^>(X) (*unija skupova je komutativna*)
| Citat: | | Ne da ti se pisati? |
Ubuduće budem.
Mislio sam da se tebi neće dati čitati ako to napišem tu,pa opet naniže. 
| Citat: | | (Vennovi dijagrami ovdje ne pomažu ;-p ) |
A nekaj sa slikama bumo smislili...
| Citat: | | Citat: | | slika nekog skupa(podskupa domene) je uvijek neprazan skup pa 'a' postoji. |
Argh. Netočno.
Da raščistimo to već jednom. Kad ti dokazuješ da je S podskup od T , ti _pretpostaviš_ x@S i iz toga nastojiš zaključiti x@T . Nigdje ti ne treba da S != 0 , odnosno da je tvoja pretpostavka stvarno ispunjiva. Štoviše, kad je univerzalno lažna ( S=0 ), tvoj posao je tim laši, jer implikacija tim trivijalnije vrijedi. |
E to mi je trebalo,dakle ja PRETPOSTAVIM da imam element u skupu S,a zašto to nije pogrešno,jer(kako kažeš) laž povlači bilo što.Oj logiko,nelogična li si. 
Dragocjeno.
| Citat: | | Citat: | Citat:
Def.slike⇒postoji b@XnY sa svojstvom f(b)=a |
Vidim da si odustao od "definicija...⇔"-stila i prešao na "⇒"-stil. Bolje, ali još uvijek nedovoljno dobro. Definicije su ovdje pomoćne tvrdnje koje koristiš da bi izgradio lanac implikacija, ne same karike. One su cement, ne cigle. |
Ok,od sada sve pišim u liniji.
Uglavnom,pisao sam ti to jedno ispod drugog radi preglednosti,svaki izraz 'def.nešto' se nadovezivao na prethodnu konkluziju,ma dobro,da ne kompliciram,ako smo precizni ko neurokirurgija onda i ostanimo takvi...da pacijenti dulje požive:-s 
| Citat: | | Citat: | Citat:
Ukoliko ne bi koristio kontraprimjer što pobija jednakost,morao bi opovrgnuti inkluziju:f(X)nf(Y) C= f(XnY) ,kako ovo srušiti ? |
Istim kontraprimjerom. (Naravno, budući da se za skupove jednakost sastoji od dvije inkluzije, a jednu si dokazao da vrijedi, zapravo i ne možeš opovrgnuti išta drugo. : ) |
Dakle nemoguće je ''simbolički''(općim zapisom) srušiti gornju inkluziju,raspisivanjem doći do kontradikcije ? 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 20:59 uto, 7. 12. 2004 Naslov: Postano: 20:59 uto, 7. 12. 2004 Naslov: |
    |
|
|
(Opaska:da su brojevi skupovi,da se naslutiti iz simbolike: f(7)=f({7}) )
[color=green]Zadatak:Nađite konkretne skupove A i B i f:A->B , X,Y C= A sa svojstvom f(XnY) C f(X)nf(Y)[/color]
Rj.:
f:IR->IR , f(x)=x^2 , X={-1},Y={1}
XnY=0=>f(XnY)=0
f(X)=1
f(Y)=1
f(X)nf(Y)=1
zaključak: 0 C {1}
Koji je najefektniji način za kreiranje protuprimjera ?Da li jednostavno ''lutanje misli'' po Kartezijevom k.sustavu ?
Postoji još jedno zanimljivo svojstvo slike koje nije spomenuto u propoziciji,a govori o ''ponašanju slike'' s obzirom na skupovnu razliku...
U gornu propoziciju nije navedeno još jedno svojstvo slike odnosno ''njeno ponašanje'' s obzirom na skupovnu razliku,za domaći uradak je dano da se uspostavi točna relacija između f(X/Y) i f(X)/f(Y) ,pa probao sam:
Kako je destrukcija lakša od izgradnje idem pokušati oboriti kontraprimjerom ovaj izraz:f(X/Y)=f(X)/f(Y) :
Kontraprimjer: Uzimam realnu funkciju f realne varijable definirane propisom f(x)=1 ,konstanta
X=<1,2>
Y=<3,4>
f(X)={1}
f(Y)={1}
=>f(X)/f(Y)=0
X/Y=<1,2>=>f(X/Y)={1}
Zaključak: f(X/Y)!=f(X)/f(Y) jer {1}!=0
Idem sada dokazati da vrijedi inkluzija f(X)/f(Y) C= f(X/Y) :
Po definiciji podskupa svaki element skupa f(X)/f(Y) mora biti i element skupa f(X/Y) pa uzmem proizvoljan element skupa f(X)/f(Y) i idem dokazati da je on nužno u skupu f(X/Y) :
Proizvoljan a@f(X)/f(Y) ,b: f(b)=a =>(*definicija skupovne razlike*)a@f(X) i a!@f(Y)=>(*definicija slike skupa po funkciji*)postoji b@X t.d. f(b)=a i nePostoji c@Y t.d. f(c)=a(ekvivalentno:Ac@Y f(c)!=a)=>b@X i b!@Y(jer svaki element skupa Y ima svojstvo da djelovanjem funkcije nad njim preslikavanje ''ne ide'' u element a ,a element b ima upravo to svojstvo)=>(*definicija skupovne razlike*)b@X/Y=>(*definicija slike*)f(b)=a@f(X/Y) CUBE;)
Ne mogu vjerovati ali uspjevam dokazati i f(X\Y) C= f(X)\f(Y) :
a@f(X\Y) , b: f(b)=a =>(*definicija slike skupa po funkciji*)postoji b@X\Y sa svojstvom f(b)=a =>b@X i b!@Y=>f(b)@f(X) i f(b)!@f(Y)
(b@X i b!@Y=>f(b)!@f(Y)
dokaz:metodom kontradikcije:
f(b)@f(Y) =>postoji b@Y t.d. f(b)@Y kontradikcija)
=>f(b)@f(X)\f(Y) CUBE;)
(Opaska:da su brojevi skupovi,da se naslutiti iz simbolike: f(7)=f({7}) )
Zadatak:Nađite konkretne skupove A i B i f:A→B , X,Y C= A sa svojstvom f(XnY) C f(X)nf(Y)
Rj.:
f:IR→IR , f(x)=x^2 , X={-1},Y={1}
XnY=0⇒f(XnY)=0
f(X)=1
f(Y)=1
f(X)nf(Y)=1
zaključak: 0 C {1}
Koji je najefektniji način za kreiranje protuprimjera ?Da li jednostavno ''lutanje misli'' po Kartezijevom k.sustavu ?
Postoji još jedno zanimljivo svojstvo slike koje nije spomenuto u propoziciji,a govori o ''ponašanju slike'' s obzirom na skupovnu razliku...
U gornu propoziciju nije navedeno još jedno svojstvo slike odnosno ''njeno ponašanje'' s obzirom na skupovnu razliku,za domaći uradak je dano da se uspostavi točna relacija između f(X/Y) i f(X)/f(Y) ,pa probao sam:
Kako je destrukcija lakša od izgradnje idem pokušati oboriti kontraprimjerom ovaj izraz:f(X/Y)=f(X)/f(Y) :
Kontraprimjer: Uzimam realnu funkciju f realne varijable definirane propisom f(x)=1 ,konstanta
X=<1,2>
Y=<3,4>
f(X)={1}
f(Y)={1}
⇒f(X)/f(Y)=0
X/Y=<1,2>⇒f(X/Y)={1}
Zaključak: f(X/Y)!=f(X)/f(Y) jer {1}!=0
Idem sada dokazati da vrijedi inkluzija f(X)/f(Y) C= f(X/Y) :
Po definiciji podskupa svaki element skupa f(X)/f(Y) mora biti i element skupa f(X/Y) pa uzmem proizvoljan element skupa f(X)/f(Y) i idem dokazati da je on nužno u skupu f(X/Y) :
Proizvoljan a@f(X)/f(Y) ,b: f(b)=a ⇒(*definicija skupovne razlike*)a@f(X) i a!@f(Y)⇒(*definicija slike skupa po funkciji*)postoji b@X t.d. f(b)=a i nePostoji c@Y t.d. f(c)=a(ekvivalentno:Ac@Y f(c)!=a)⇒b@X i b!@Y(jer svaki element skupa Y ima svojstvo da djelovanjem funkcije nad njim preslikavanje ''ne ide'' u element a ,a element b ima upravo to svojstvo)⇒(*definicija skupovne razlike*)b@X/Y⇒(*definicija slike*)f(b)=a@f(X/Y) CUBE;)
Ne mogu vjerovati ali uspjevam dokazati i f(X\Y) C= f(X)\f(Y) :
a@f(X\Y) , b: f(b)=a ⇒(*definicija slike skupa po funkciji*)postoji b@X\Y sa svojstvom f(b)=a ⇒b@X i b!@Y⇒f(b)@f(X) i f(b)!@f(Y)
(b@X i b!@Y⇒f(b)!@f(Y)
dokaz:metodom kontradikcije:
f(b)@f(Y) ⇒postoji b@Y t.d. f(b)@Y kontradikcija)
⇒f(b)@f(X)\f(Y) CUBE;)
_________________
Samo sam jedan čovjek,
samo jedan pakao.
Zadnja promjena: Vincent Van Ear; 12:23 čet, 9. 12. 2004; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 12:53 sri, 8. 12. 2004 Naslov: Postano: 12:53 sri, 8. 12. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"](Opaska:da su brojevi skupovi,da se naslutiti iz simbolike: f(7)=f({7}) )
[/quote]
Ne mislim ulaziti u ovu raspravu, nego samo malo pojasniti gornju konstataciju.
Prvo pitanje simbolike f(7) = f({7})
To dolazi zbog toga sto za jednoclane skupove vrijedi f({x})={f(x)}, pa ljudi bas i ne vole pisati te viticaste zagrade, ali ustvari su f(7) i f({7}) dva razlicita objekta, jer kada bi bili jednaki imali bi f(7)=f({7})={f(7)}, pa fi f(7) bio skup koji sadrzi sam sebe kao element, sto je nemoguce.
Drugo brojevi su skupovi:(Samo za prirodne brojeve, za detaljniju raspravu bilo bi pozeljno otvoriti poseban topic.)
Dakle ovako:
[latex]0 = \emptyset[/latex]
[latex]1 = \{ \emptyset \}[/latex]
[latex]2 = \{ \emptyset, \{ \emptyset \} \}[/latex]
[latex]3 = \{ \emptyset,\{ \emptyset \} ,\{ \emptyset, \{ \emptyset \} \} \} [/latex]
I tako dalje, odnosno [latex]n+1 = \{0, 1, 2, \ldots, n \}[/latex]
Jos mala napomena, ako imamo funkciju f cija su domena prirodni brojevi, onda imamo f(7) = f({0, 1, 2, 3, 4, 5, 6}), pa je na prvi pogled moguca zabuna da li se govori o vrijednosti funkcije za argument 7, ili o slici skupa {0, 1, ... ,6} :grebgreb: ali je jasno da do tog problema u praksi nikada nece doci jer je gotovo uvijek iz konteksta jasno na sto se misli, a ako i nije moze se napomeniti ili mozda uvesti bolja simbolika. :wink:
| Vincent Van Ear (napisa): | (Opaska:da su brojevi skupovi,da se naslutiti iz simbolike: f(7)=f({7}) )
|
Ne mislim ulaziti u ovu raspravu, nego samo malo pojasniti gornju konstataciju.
Prvo pitanje simbolike f(7) = f({7})
To dolazi zbog toga sto za jednoclane skupove vrijedi f({x})={f(x)}, pa ljudi bas i ne vole pisati te viticaste zagrade, ali ustvari su f(7) i f({7}) dva razlicita objekta, jer kada bi bili jednaki imali bi f(7)=f({7})={f(7)}, pa fi f(7) bio skup koji sadrzi sam sebe kao element, sto je nemoguce.
Drugo brojevi su skupovi:(Samo za prirodne brojeve, za detaljniju raspravu bilo bi pozeljno otvoriti poseban topic.)
Dakle ovako:
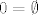
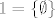
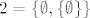
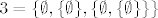
I tako dalje, odnosno 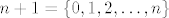
Jos mala napomena, ako imamo funkciju f cija su domena prirodni brojevi, onda imamo f(7) = f({0, 1, 2, 3, 4, 5, 6}), pa je na prvi pogled moguca zabuna da li se govori o vrijednosti funkcije za argument 7, ili o slici skupa {0, 1, ... ,6}  ali je jasno da do tog problema u praksi nikada nece doci jer je gotovo uvijek iz konteksta jasno na sto se misli, a ako i nije moze se napomeniti ili mozda uvesti bolja simbolika. ali je jasno da do tog problema u praksi nikada nece doci jer je gotovo uvijek iz konteksta jasno na sto se misli, a ako i nije moze se napomeniti ili mozda uvesti bolja simbolika. 
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 12:00 čet, 9. 12. 2004 Naslov: Postano: 12:00 čet, 9. 12. 2004 Naslov: |
    |
|
|
[quote] To dolazi zbog toga sto za jednoclane skupove vrijedi f({x})={f(x)}, pa ljudi bas i ne vole pisati te viticaste zagrade, ali ustvari su f(7) i f({7}) dva razlicita objekta, jer kada bi bili jednaki imali bi f(7)=f({7})={f(7)}, pa fi f(7) bio skup koji sadrzi sam sebe kao element, sto je nemoguce. [/quote]
Hvala.
[quote] Drugo brojevi su skupovi:(Samo za prirodne brojeve, za detaljniju raspravu bilo bi pozeljno otvoriti poseban topic.)
Dakle ovako:
I tako dalje, odnosno [/quote]
:shocked!: Najbolje da o ovome još ne razmišljam. :whistle:
| Citat: | | To dolazi zbog toga sto za jednoclane skupove vrijedi f({x})={f(x)}, pa ljudi bas i ne vole pisati te viticaste zagrade, ali ustvari su f(7) i f({7}) dva razlicita objekta, jer kada bi bili jednaki imali bi f(7)=f({7})={f(7)}, pa fi f(7) bio skup koji sadrzi sam sebe kao element, sto je nemoguce. |
Hvala.
| Citat: | Drugo brojevi su skupovi:(Samo za prirodne brojeve, za detaljniju raspravu bilo bi pozeljno otvoriti poseban topic.)
Dakle ovako:
I tako dalje, odnosno |
 Najbolje da o ovome još ne razmišljam. Najbolje da o ovome još ne razmišljam. 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 15:18 čet, 9. 12. 2004 Naslov: Postano: 15:18 čet, 9. 12. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"]pa vidiš i sam kako me taj skup sramoti :shocked!: :o) .[/quote]
Pa sramoti te najvećim dijelom upravo zato što ga smatraš posebnim... :-/
[quote][quote]f^>(0)=0 (slika praznog skupa je prazan skup),[/quote]
Ima li imalo sugestivnosti u oznaci slike ili ju ja jednostavno ne razaznajem ? :o)[/quote]
Ne znam. Probaj ovo: [latex]f^\rangle(\emptyset)[/latex]. To sugestivno?
[quote]Htjede su uvjeriti da sam doista uzeo nešto ''opipljivo'' iz skupa f(XuY)... :-k ...wrong,neznam kako mi napamet nije palo da X i Y mogu biti prazni...[/quote]
Kao što rekoh gore, to ti uopće ne treba pasti na pamet (u većini ovakvih dokaza) ako ne ideš "raspisivati posebne slučajeve". U mathu nema _zapravo_ posebnih slučajeva (koji nisu samo trivijalne instance nečeg općeg)... svi su oni tu sa svrhom. Samo što mnoge od tih svrhâ još ne vidiš. ;-|
[quote]Pretpostavljam da ovdje nije bilo nužno(za razliku od slike praznog skupa,gdje je ona morala biti naznačena drukčije od f(0) što bi upućivalo na vrijednost funkcije u točki 0) pisati sliku kao f^>(X) već jednostavnije f(X) s obzirom da smo se dogovorili da ćemo skupove označavati velikim slovima engleskog alfabeta.[/quote]
Pa ništa nije nužno u notaciji, ako te onaj na drugom kraju razumije. :-) No:
1. Dobro je imati jednu oznaku za f koja djeluje na "točke", a drugu za f koja djeluje na skupove. Na kraju krajeva, jedno je :S->T , a drugo je zapravo :\P(S)->\P(T) (jer podskupovima od S pridružuje podskupove od T ).
2. 0 kao oznaka za prazan skup samo je specijalan slučaj (iako zasad vjerojatno jedini koji bi te mogao zanimati). Jednako tako je 1 oznaka za {0} ... no možda bolje da zasad :-# o tome. ;-)
3. Velika engleska slova su samo sugestija, i to ne neka koja se baš rigorozno provodi. Gle rastav na parcijalne razlomke uostalom. :-)
4. Kao što mdoko reče, sve su ionako skupovi. Dakle, bilo bi dobro razlikovati f(nešto) kad je nešto shvaćeno kao element domene, od toga kad je shvaćeno kao podskup domene -- što je posebno izraženo kad je domena tzv. tranzitivan skup: skup čiji je svaki element ujedno i njegov podskup. ;-) (I o ovome je bolje da ne razmišljaš puno... zasad.; )
[quote][quote] Ne da ti se pisati? [/quote]
Ubuduće budem.
Mislio sam da se tebi neće dati čitati ako to napišem tu,pa opet naniže. :-P [/quote]
Da se _meni_ nešto ne da čitati? Sanjaj. ;-P
[quote][quote] (Vennovi dijagrami ovdje ne pomažu ;-p )[/quote]
A nekaj sa slikama bumo smislili...#-o[/quote]
Sretno ti bilo... ;-)
[quote] laž povlači bilo što.Oj logiko,nelogična li si. :mrgreen:[/quote]
Gr. Ajde, što bi po tvome bilo logičnije od toga? Dizajniraj tablicu istinitosti za implikaciju onako kako bi ti htio da izgleda. Kladim se da ću ti naći daleko više nelogičnosti u njoj. ;-P
[quote]Ok,od sada sve pišim u liniji.
Uglavnom,pisao sam ti to jedno ispod drugog radi preglednosti,svaki izraz 'def.nešto' se nadovezivao na prethodnu konkluziju,ma dobro,da ne kompliciram,ako smo precizni ko neurokirurgija onda i ostanimo takvi...da pacijenti dulje požive:-s :kuckkuck:[/quote]
Ma gle... jasno mi je da je ovaj medij jedno, a papir drugo... upravo zato dajem hintove kako (ne)pisati i po jednom i po drugom, da se shvati... na papiru bi to vjerojatno izgledalo ok.
[quote][quote] Citat:
Ukoliko ne bi koristio kontraprimjer što pobija jednakost,morao bi opovrgnuti inkluziju:f(X)nf(Y) C= f(XnY) ,kako ovo srušiti ? [/quote]
Dakle nemoguće je ''simbolički''(općim zapisom) srušiti gornju inkluziju,raspisivanjem doći do kontradikcije ? :-k[/quote]
Naravno. Kad bi ju "općim zapisom" bilo moguće srušiti, to bi značilo da je moguće dokazati njenu negaciju u općem slučaju, odnosno da _općenito_ vrijedi da f^>(X)nf^>(Y)(!C=)f^>(XnY) . A to naravno nije. Najjednostavniji primjer je valjda s praznim skupom ;-PP , no možemo proći i bez njega. Stavi f=identiteta , npr.
Shvaćaš razliku između "tvrdnja ne (.vrijedi općenito.)" (ie, postoji slučaj u kojem ne vrijedi), i "tvrdnja (.ne vrijedi.) općenito" (ie, nikada ne vrijedi)?
| Vincent Van Ear (napisa): | pa vidiš i sam kako me taj skup sramoti   . . |
Pa sramoti te najvećim dijelom upravo zato što ga smatraš posebnim... :-/
| Citat: | | Citat: | | f^>(0)=0 (slika praznog skupa je prazan skup), |
Ima li imalo sugestivnosti u oznaci slike ili ju ja jednostavno ne razaznajem ?  |
Ne znam. Probaj ovo: 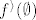 . To sugestivno? . To sugestivno?
| Citat: | Htjede su uvjeriti da sam doista uzeo nešto ''opipljivo'' iz skupa f(XuY)...  ...wrong,neznam kako mi napamet nije palo da X i Y mogu biti prazni... ...wrong,neznam kako mi napamet nije palo da X i Y mogu biti prazni... |
Kao što rekoh gore, to ti uopće ne treba pasti na pamet (u većini ovakvih dokaza) ako ne ideš "raspisivati posebne slučajeve". U mathu nema _zapravo_ posebnih slučajeva (koji nisu samo trivijalne instance nečeg općeg)... svi su oni tu sa svrhom. Samo što mnoge od tih svrhâ još ne vidiš. ;-|
| Citat: | | Pretpostavljam da ovdje nije bilo nužno(za razliku od slike praznog skupa,gdje je ona morala biti naznačena drukčije od f(0) što bi upućivalo na vrijednost funkcije u točki 0) pisati sliku kao f^>(X) već jednostavnije f(X) s obzirom da smo se dogovorili da ćemo skupove označavati velikim slovima engleskog alfabeta. |
Pa ništa nije nužno u notaciji, ako te onaj na drugom kraju razumije.  No: No:
1. Dobro je imati jednu oznaku za f koja djeluje na "točke", a drugu za f koja djeluje na skupove. Na kraju krajeva, jedno je :S→T , a drugo je zapravo :\P(S)→\P(T) (jer podskupovima od S pridružuje podskupove od T ).
2. 0 kao oznaka za prazan skup samo je specijalan slučaj (iako zasad vjerojatno jedini koji bi te mogao zanimati). Jednako tako je 1 oznaka za {0} ... no možda bolje da zasad  o tome. o tome. 
3. Velika engleska slova su samo sugestija, i to ne neka koja se baš rigorozno provodi. Gle rastav na parcijalne razlomke uostalom. 
4. Kao što mdoko reče, sve su ionako skupovi. Dakle, bilo bi dobro razlikovati f(nešto) kad je nešto shvaćeno kao element domene, od toga kad je shvaćeno kao podskup domene – što je posebno izraženo kad je domena tzv. tranzitivan skup: skup čiji je svaki element ujedno i njegov podskup.  (I o ovome je bolje da ne razmišljaš puno... zasad.; ) (I o ovome je bolje da ne razmišljaš puno... zasad.; )
| Citat: | | Citat: | | Ne da ti se pisati? |
Ubuduće budem.
Mislio sam da se tebi neće dati čitati ako to napišem tu,pa opet naniže.  |
Da se _meni_ nešto ne da čitati? Sanjaj. ;-P
| Citat: | | Citat: | | (Vennovi dijagrami ovdje ne pomažu ;-p ) |
A nekaj sa slikama bumo smislili... |
Sretno ti bilo... 
| Citat: | laž povlači bilo što.Oj logiko,nelogična li si.  |
Gr. Ajde, što bi po tvome bilo logičnije od toga? Dizajniraj tablicu istinitosti za implikaciju onako kako bi ti htio da izgleda. Kladim se da ću ti naći daleko više nelogičnosti u njoj. ;-P
| Citat: | Ok,od sada sve pišim u liniji.
Uglavnom,pisao sam ti to jedno ispod drugog radi preglednosti,svaki izraz 'def.nešto' se nadovezivao na prethodnu konkluziju,ma dobro,da ne kompliciram,ako smo precizni ko neurokirurgija onda i ostanimo takvi...da pacijenti dulje požive:-s  |
Ma gle... jasno mi je da je ovaj medij jedno, a papir drugo... upravo zato dajem hintove kako (ne)pisati i po jednom i po drugom, da se shvati... na papiru bi to vjerojatno izgledalo ok.
| Citat: | | Citat: | Citat:
Ukoliko ne bi koristio kontraprimjer što pobija jednakost,morao bi opovrgnuti inkluziju:f(X)nf(Y) C= f(XnY) ,kako ovo srušiti ? |
Dakle nemoguće je ''simbolički''(općim zapisom) srušiti gornju inkluziju,raspisivanjem doći do kontradikcije ?  |
Naravno. Kad bi ju "općim zapisom" bilo moguće srušiti, to bi značilo da je moguće dokazati njenu negaciju u općem slučaju, odnosno da _općenito_ vrijedi da f^>(X)nf^>(Y)(!C=)f^>(XnY) . A to naravno nije. Najjednostavniji primjer je valjda s praznim skupom ;-PP , no možemo proći i bez njega. Stavi f=identiteta , npr.
Shvaćaš razliku između "tvrdnja ne (.vrijedi općenito.)" (ie, postoji slučaj u kojem ne vrijedi), i "tvrdnja (.ne vrijedi.) općenito" (ie, nikada ne vrijedi)?
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 16:19 čet, 9. 12. 2004 Naslov: Postano: 16:19 čet, 9. 12. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"](Opaska:da su brojevi skupovi,da se naslutiti iz simbolike: f(7)=f({7}) )[/quote]
Ne bih rekao. 7 jest skup, ali ne skup {7} . No o tome nekom drugom prilikom... :-)
[quote][color=green]Zadatak:Nađite konkretne skupove A i B i f:A->B , X,Y C= A sa svojstvom f(XnY) C f(X)nf(Y)[/color]
Rj.:
f:IR->IR , f(x)=x^2 , X={-1},Y={1}
XnY=0=>f(XnY)=0
f(X)=1
f(Y)=1
f(X)nf(Y)=1[/quote]
Eto, vidiš što se dogodi kad ne paziš na razliku između {a} i a ? :-grr.
Naravno, {1} je odgovor, ne 1 .
[quote]Koji je najefektniji način za kreiranje protuprimjera ?Da li jednostavno ''lutanje misli'' po Kartezijevom k.sustavu ?[/quote]
Opet, ovisi o tome kako ti mozak radi. Npr. meni je sasvim očito da to ima veze s injektivnošću funkcije f : ako f dvije vrijednosti preslika u istu, presjek tih dvaju singletonova bit će prazan, dok će presjek njihovih slika biti ta zajednička vrijednost. To si upravo napravio gore, no možeš to i formalizirati: probaj dokazati da ako je f injekcija, onda vrijedi jednakost u toj formuli.
Mehanički, razmišljao bi valjda ovako:
Trebam da mi presjek slikâ nije podskup slike presjeka. Dakle, trebam neki a koji jest u presjeku slikâ (dakle a@f^>(X) & a@f^>(Y) ), a nije u slici presjeka (dakle a(!@)f^>(XnY) ). Te tri tvrdnje znače:
a=f(b) za neki b@X
a=f(c) za neki c@Y
a!=f(d) , za svaki d@XnY .
Iz toga se odmah vidi da b i c ne smiju biti jednaki (inače bi bili iz XnY ), a trebaju imati jednake funkcijske vrijednosti ( a ). Dakle, f nije injekcija, i kontraprimjer leži upravo tamo gdje se dva različita broja preslikavaju u isti.
[quote]U gornu propoziciju nije navedeno još jedno svojstvo slike odnosno ''njeno ponašanje'' s obzirom na skupovnu razliku,za domaći uradak je dano da se uspostavi točna relacija između f(X/Y) i f(X)/f(Y)[/quote]
Valjda f^>(X\Y) i f^>(X)\f^>(Y) .
( "\" ti je AltGr+Q na hrvatskoj tipkovnici)
[quote]Idem sada dokazati da vrijedi inkluzija f(X)/f(Y) C= f(X/Y) :
((Kontraprimjer ok.))
((Ova gornja inkluzija -- dokaz ok.))
[quote]Ne mogu vjerovati ali uspjevam dokazati i f(X\Y) C= f(X)\f(Y) :[/quote]
Ja mogu vjerovati. :-p
[quote](b@X i b!@Y=>f(b)!@f(Y)[/quote]
Ta tvrdnja ne vrijedi. A greška u dokazu je:
[quote]f(b)@f(Y) =>postoji [color=red]b[/color]@Y t.d. f(b)@Y kontradikcija)[/quote]
Tu. (I drugdje.:-p ) Ako je f(b)@f^>(Y) , ti već imaš definiran b . Slovo b ti je potrošeno (kaže se da je varijabla b vezana), te trebaš uvesti novo za raspisati tvrdnju. Dakle (Ec@Y)(f(b)=f(c)) . I sad, naravno, c@Y , i f(b)=f(c) , no iz toga ne slijedi c=b , odnosno b@Y . :-/
| Vincent Van Ear (napisa): | | (Opaska:da su brojevi skupovi,da se naslutiti iz simbolike: f(7)=f({7}) ) |
Ne bih rekao. 7 jest skup, ali ne skup {7} . No o tome nekom drugom prilikom... 
| Citat: | Zadatak:Nađite konkretne skupove A i B i f:A→B , X,Y C= A sa svojstvom f(XnY) C f(X)nf(Y)
Rj.:
f:IR→IR , f(x)=x^2 , X={-1},Y={1}
XnY=0⇒f(XnY)=0
f(X)=1
f(Y)=1
f(X)nf(Y)=1 |
Eto, vidiš što se dogodi kad ne paziš na razliku između {a} i a ? :-grr.
Naravno, {1} je odgovor, ne 1 .
| Citat: | | Koji je najefektniji način za kreiranje protuprimjera ?Da li jednostavno ''lutanje misli'' po Kartezijevom k.sustavu ? |
Opet, ovisi o tome kako ti mozak radi. Npr. meni je sasvim očito da to ima veze s injektivnošću funkcije f : ako f dvije vrijednosti preslika u istu, presjek tih dvaju singletonova bit će prazan, dok će presjek njihovih slika biti ta zajednička vrijednost. To si upravo napravio gore, no možeš to i formalizirati: probaj dokazati da ako je f injekcija, onda vrijedi jednakost u toj formuli.
Mehanički, razmišljao bi valjda ovako:
Trebam da mi presjek slikâ nije podskup slike presjeka. Dakle, trebam neki a koji jest u presjeku slikâ (dakle a@f^>(X) & a@f^>(Y) ), a nije u slici presjeka (dakle a(!@)f^>(XnY) ). Te tri tvrdnje znače:
a=f(b) za neki b@X
a=f(c) za neki c@Y
a!=f(d) , za svaki d@XnY .
Iz toga se odmah vidi da b i c ne smiju biti jednaki (inače bi bili iz XnY ), a trebaju imati jednake funkcijske vrijednosti ( a ). Dakle, f nije injekcija, i kontraprimjer leži upravo tamo gdje se dva različita broja preslikavaju u isti.
| Citat: | | U gornu propoziciju nije navedeno još jedno svojstvo slike odnosno ''njeno ponašanje'' s obzirom na skupovnu razliku,za domaći uradak je dano da se uspostavi točna relacija između f(X/Y) i f(X)/f(Y) |
Valjda f^>(X\Y) i f^>(X)\f^>(Y) .
( "\" ti je AltGr+Q na hrvatskoj tipkovnici)
[quote]Idem sada dokazati da vrijedi inkluzija f(X)/f(Y) C= f(X/Y) :
((Kontraprimjer ok.))
((Ova gornja inkluzija – dokaz ok.))
| Citat: | | Ne mogu vjerovati ali uspjevam dokazati i f(X\Y) C= f(X)\f(Y) : |
Ja mogu vjerovati. :-p
| Citat: | | (b@X i b!@Y⇒f(b)!@f(Y) |
Ta tvrdnja ne vrijedi. A greška u dokazu je:
| Citat: | | f(b)@f(Y) ⇒postoji b@Y t.d. f(b)@Y kontradikcija) |
Tu. (I drugdje.:-p ) Ako je f(b)@f^>(Y) , ti već imaš definiran b . Slovo b ti je potrošeno (kaže se da je varijabla b vezana), te trebaš uvesti novo za raspisati tvrdnju. Dakle (Ec@Y)(f(b)=f(c)) . I sad, naravno, c@Y , i f(b)=f(c) , no iz toga ne slijedi c=b , odnosno b@Y . :-/
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 16:22 čet, 9. 12. 2004 Naslov: Postano: 16:22 čet, 9. 12. 2004 Naslov: |
    |
|
|
[quote="mdoko"]na prvi pogled moguca zabuna da li se govori o vrijednosti funkcije za argument 7, ili o slici skupa {0, 1, ... ,6} :grebgreb: ali je jasno da do tog problema u praksi nikada nece doci jer je gotovo uvijek iz konteksta jasno na sto se misli, a ako i nije moze se napomeniti ili mozda uvesti bolja simbolika. :wink:[/quote]
Ne znam ja što ti smatraš "praksom"... :-) U analizi možda i neće, no u teoriji skupova takve stvari se svakodnevno događaju. Da, treba nam bolja simbolika. :-)
| mdoko (napisa): | na prvi pogled moguca zabuna da li se govori o vrijednosti funkcije za argument 7, ili o slici skupa {0, 1, ... ,6}  ali je jasno da do tog problema u praksi nikada nece doci jer je gotovo uvijek iz konteksta jasno na sto se misli, a ako i nije moze se napomeniti ili mozda uvesti bolja simbolika. ali je jasno da do tog problema u praksi nikada nece doci jer je gotovo uvijek iz konteksta jasno na sto se misli, a ako i nije moze se napomeniti ili mozda uvesti bolja simbolika.  |
Ne znam ja što ti smatraš "praksom"...  U analizi možda i neće, no u teoriji skupova takve stvari se svakodnevno događaju. Da, treba nam bolja simbolika. U analizi možda i neće, no u teoriji skupova takve stvari se svakodnevno događaju. Da, treba nam bolja simbolika. 
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 8:23 pet, 10. 12. 2004 Naslov: Postano: 8:23 pet, 10. 12. 2004 Naslov: |
    |
|
|
[quote] Pa sramoti te najvećim dijelom upravo zato što ga smatraš posebnim... :-/[/quote]
Dobro,probat ću ga mentalno komercijalizirati bez obzira što je on _kolekcija ničega_ .
[quote] [quote] [quote]Citat:
Citat:
f^>(0)=0 (slika praznog skupa je prazan skup), [/quote]
Ima li imalo sugestivnosti u oznaci slike ili ju ja jednostavno ne razaznajem ? [/quote]
Ne znam. Probaj ovo: . To sugestivno? [/quote]
Je.
Jelda ti ''fornije'' pisati ''normalno'' nego u toj skripti ?
Mislim,što te sprečava u pisanju skripte nego navika samog kuckanja bez nekih regula...
[quote] \P(S)->\P(T)[/quote]
\P je oznaka za partitivni skup,samo što bi P trebalo biti 'pisano P',dakle _lijepo_ slovo P.
Imam bolju,intuivniju oznaku: JP
,gdje da se javim za prihvaćanje oznake kao službene u internet komunikaciji ? :wicked:
[quote] Jednako tako je 1 oznaka za {0} ... no možda bolje da zasad o tome. [/quote]
Da,bolje je.
Ne upropastimo gledatelju rasplet filma prije nego je upoznao atmosferu istoga.
Tek sam sjeo u kinu i načeo kokice.;)
A i već ovaj foršpan što si ga dao može u gledatelju izazvati mučninu zbog nadasve degutantno-šokatne scene u kojoj je broj 1 zapravo... :crazyeyes: :crazy: ...
to je kao,učenje matematike ispočetka,dođe ti profać i kaže:
-ok,dosad smo smatrali da je 1 samo jedan groš,čovjek,pas,oblak,duh,teorem...sve je to dio velike vladine urote zataškavanja i zato se primite čvrsto za sjedalice(mozgove):1 je zapravo skup što sadrži...
[quote] sve su ionako skupovi[/quote]
Ovo ću si istetovirati na čelo dovoljno duboko da i mozak osjeti :o)
[quote][quote]
Citat:
laž povlači bilo što.Oj logiko,nelogična li si. [/quote]
Gr. Ajde, što bi po tvome bilo logičnije od toga? [/quote]
Ma dovoljno je ovo:
Iz pretpostavke da _govorim istinu_ ne mogu povući(izreći) nikakvu laž.
Slažem se.
Iz pretpostavke da _govorim laž_ mogu povući(izreći) nekakvu istinu.
Kako,ako ''lažem k'o pas'' ?
[quote] Shvaćaš razliku između "tvrdnja ne (.vrijedi općenito.)" (ie, postoji slučaj u kojem ne vrijedi), i "tvrdnja (.ne vrijedi.) općenito" (ie, nikada ne vrijedi)?[/quote]
Sada da,hvala.
[quote] probaj dokazati da ako je f injekcija, onda vrijedi jednakost u toj formuli.[/quote]
Pretpostavke: f:A->B ,injekcija
Tvrdnja: Za X,Y C= A vrijedi: f^>(XnY)=f^>(X)nf^>(Y)
Dokaz(po definiciji jednakosti skupova):
Tvrdnja:f^>(XnY) C= f^>(X)nf^>(Y)
(ova tvrdnja se dokazuje i bez zahtjevanja da je funkcija injekcija,ona vrijedi općenito za svaku funkciju)
Dokaz(po definiciji 'biti podskup'):
Proizvoljan a@f^>(XnY) , b:f(b)=a =>(*definicija slike*)postoji b@XnY sa svojstvom f(b)=a =>(*definicija presjeka*)b@X i b@Y=>(*definicija slike*)f(b)@f^>(X) i f(b)@f^>(Y)=>(*definicija presjeka*)f(b)=a@f^>(X)nf^>(Y) CUBE;)
Tvrdnja:f^>(X)nf^>(Y) C= f^>(XnY)
Dokaz(po definiciji 'biti podskup'):
Proizvoljan a@f^>(X)nf^>(Y) ,b:f(b)=a , c:f(c)=a =>(*definicija presjeka*)a@f^>(X) i a@f^>(Y)=>(*definicija slike*)postoji b@X sa svojstvom f(b)=a i postoji c@Y sa svojstvom f(c)=a=>(*svojstvo injektivne funkcije:jednakost slika u točkama povlači jednakost točaka)b@XnY(*mogli uzeti i točku c*)=>f(b)=a@f^>(XnY) CUBE;)
[quote] Mehanički, razmišljao bi valjda ovako:
Trebam da mi presjek slikâ nije podskup slike presjeka. Dakle, trebam neki a koji jest u presjeku slikâ (dakle a@f^>(X) & a@f^>(Y) ), a nije u slici presjeka (dakle a(!@)f^>(XnY) ). Te tri tvrdnje znače:
a=f(b) za neki b@X
a=f(c) za neki c@Y
a!=f(d) , za svaki d@XnY .
Iz toga se odmah vidi da b i c ne smiju biti jednaki (inače bi bili iz XnY ), a trebaju imati jednake funkcijske vrijednosti ( a ). Dakle, f nije injekcija, i kontraprimjer leži upravo tamo gdje se dva različita broja preslikavaju u isti.[/quote]
Sviđa mi se ovaj način razmišljanja.
Smijem li vidjeti kako razmišljaš u situaciji:
vrijedi li jednakost,lijeva ili desna inkluzija?Između skupova:
f^>(X\Y) i f^>(X)\f^>(Y) .
[quote] b@X i b!@Y=>f(b)!@f(Y) [/quote]
ironično je(i prejednostavno za pobiti već intuitivno u glavi) da mi je kontraprimjer za to upravo onaj kojeg sam konstruirao:
f:IR->IR , f(x)=1
X=<1,2>
Y=<3,4>
b=3/2 =>f(b)=1=>f(b)@f(Y)={1}
[quote][quote] Citat:
(b@X i b!@Y=>f(b)!@f(Y) [/quote]
Ta tvrdnja ne vrijedi. A greška u dokazu je:[/quote]
Sorry ako ću djelovati iritantno ali nismo li negdje već rekli da je tvrdnja nešto već dokazano.
Nisi li htio reći da _hipoteza_ ne vrijedi :?: :?
P.S.:
vidim da imaš novi sig,ne sviđa ti se ono što vidiš oko sebe...josh da gledaš telku tek bi vidio koliko je ta kost oglobana...
a i svakako vidim da si promijenio lokaciju. :D
| Citat: | | Pa sramoti te najvećim dijelom upravo zato što ga smatraš posebnim... :-/ |
Dobro,probat ću ga mentalno komercijalizirati bez obzira što je on _kolekcija ničega_ .
| Citat: | | Citat: | | Citat: | Citat:
Citat:
f^>(0)=0 (slika praznog skupa je prazan skup), |
Ima li imalo sugestivnosti u oznaci slike ili ju ja jednostavno ne razaznajem ? |
Ne znam. Probaj ovo: . To sugestivno? |
Je.
Jelda ti ''fornije'' pisati ''normalno'' nego u toj skripti ?
Mislim,što te sprečava u pisanju skripte nego navika samog kuckanja bez nekih regula...
\P je oznaka za partitivni skup,samo što bi P trebalo biti 'pisano P',dakle _lijepo_ slovo P.
Imam bolju,intuivniju oznaku: JP
,gdje da se javim za prihvaćanje oznake kao službene u internet komunikaciji ? 
| Citat: | | Jednako tako je 1 oznaka za {0} ... no možda bolje da zasad o tome. |
Da,bolje je.
Ne upropastimo gledatelju rasplet filma prije nego je upoznao atmosferu istoga.
Tek sam sjeo u kinu i načeo kokice.
A i već ovaj foršpan što si ga dao može u gledatelju izazvati mučninu zbog nadasve degutantno-šokatne scene u kojoj je broj 1 zapravo...   ... ...
to je kao,učenje matematike ispočetka,dođe ti profać i kaže:
-ok,dosad smo smatrali da je 1 samo jedan groš,čovjek,pas,oblak,duh,teorem...sve je to dio velike vladine urote zataškavanja i zato se primite čvrsto za sjedalice(mozgove):1 je zapravo skup što sadrži...
| Citat: | | sve su ionako skupovi |
Ovo ću si istetovirati na čelo dovoljno duboko da i mozak osjeti 
| Citat: | | Citat: |
Citat:
laž povlači bilo što.Oj logiko,nelogična li si. |
Gr. Ajde, što bi po tvome bilo logičnije od toga? |
Ma dovoljno je ovo:
Iz pretpostavke da _govorim istinu_ ne mogu povući(izreći) nikakvu laž.
Slažem se.
Iz pretpostavke da _govorim laž_ mogu povući(izreći) nekakvu istinu.
Kako,ako ''lažem k'o pas'' ?
| Citat: | | Shvaćaš razliku između "tvrdnja ne (.vrijedi općenito.)" (ie, postoji slučaj u kojem ne vrijedi), i "tvrdnja (.ne vrijedi.) općenito" (ie, nikada ne vrijedi)? |
Sada da,hvala.
| Citat: | | probaj dokazati da ako je f injekcija, onda vrijedi jednakost u toj formuli. |
Pretpostavke: f:A→B ,injekcija
Tvrdnja: Za X,Y C= A vrijedi: f^>(XnY)=f^>(X)nf^>(Y)
Dokaz(po definiciji jednakosti skupova):
Tvrdnja:f^>(XnY) C= f^>(X)nf^>(Y)
(ova tvrdnja se dokazuje i bez zahtjevanja da je funkcija injekcija,ona vrijedi općenito za svaku funkciju)
Dokaz(po definiciji 'biti podskup'):
Proizvoljan a@f^>(XnY) , b:f(b)=a ⇒(*definicija slike*)postoji b@XnY sa svojstvom f(b)=a ⇒(*definicija presjeka*)b@X i b@Y⇒(*definicija slike*)f(b)@f^>(X) i f(b)@f^>(Y)⇒(*definicija presjeka*)f(b)=a@f^>(X)nf^>(Y) CUBE;)
Tvrdnja:f^>(X)nf^>(Y) C= f^>(XnY)
Dokaz(po definiciji 'biti podskup'):
Proizvoljan a@f^>(X)nf^>(Y) ,b:f(b)=a , c:f(c)=a ⇒(*definicija presjeka*)a@f^>(X) i a@f^>(Y)⇒(*definicija slike*)postoji b@X sa svojstvom f(b)=a i postoji c@Y sa svojstvom f(c)=a⇒(*svojstvo injektivne funkcije:jednakost slika u točkama povlači jednakost točaka)b@XnY(*mogli uzeti i točku c*)⇒f(b)=a@f^>(XnY) CUBE;)
| Citat: | Mehanički, razmišljao bi valjda ovako:
Trebam da mi presjek slikâ nije podskup slike presjeka. Dakle, trebam neki a koji jest u presjeku slikâ (dakle a@f^>(X) & a@f^>(Y) ), a nije u slici presjeka (dakle a(!@)f^>(XnY) ). Te tri tvrdnje znače:
a=f(b) za neki b@X
a=f(c) za neki c@Y
a!=f(d) , za svaki d@XnY .
Iz toga se odmah vidi da b i c ne smiju biti jednaki (inače bi bili iz XnY ), a trebaju imati jednake funkcijske vrijednosti ( a ). Dakle, f nije injekcija, i kontraprimjer leži upravo tamo gdje se dva različita broja preslikavaju u isti. |
Sviđa mi se ovaj način razmišljanja.
Smijem li vidjeti kako razmišljaš u situaciji:
vrijedi li jednakost,lijeva ili desna inkluzija?Između skupova:
f^>(X\Y) i f^>(X)\f^>(Y) .
| Citat: | | b@X i b!@Y⇒f(b)!@f(Y) |
ironično je(i prejednostavno za pobiti već intuitivno u glavi) da mi je kontraprimjer za to upravo onaj kojeg sam konstruirao:
f:IR→IR , f(x)=1
X=<1,2>
Y=<3,4>
b=3/2 ⇒f(b)=1⇒f(b)@f(Y)={1}
| Citat: | | Citat: | Citat:
(b@X i b!@Y⇒f(b)!@f(Y) |
Ta tvrdnja ne vrijedi. A greška u dokazu je: |
Sorry ako ću djelovati iritantno ali nismo li negdje već rekli da je tvrdnja nešto već dokazano.
Nisi li htio reći da _hipoteza_ ne vrijedi  
P.S.:
vidim da imaš novi sig,ne sviđa ti se ono što vidiš oko sebe...josh da gledaš telku tek bi vidio koliko je ta kost oglobana...
a i svakako vidim da si promijenio lokaciju. 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 12:10 pet, 10. 12. 2004 Naslov: Postano: 12:10 pet, 10. 12. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"][quote] Pa sramoti te najvećim dijelom upravo zato što ga smatraš posebnim... :-/[/quote]
Dobro,probat ću ga mentalno komercijalizirati bez obzira što je on _kolekcija ničega_ .[/quote]
Štogod. Da si bio na mojim vježbama, uvjeren sam da ne bi skupove smatrao kolekcijama. :->
[quote]Jelda ti ''fornije'' pisati ''normalno'' nego u toj skripti ?
Mislim,što te sprečava u pisanju skripte nego navika samog kuckanja bez nekih regula...[/quote]
Ovisi koliko ozbiljno shvatiš "regule". Jedino što me _zapravo_ nervira je pisanje [ latex ] i [/ latex ] tagova. Puno bih sretniji bio s jednostavnim $ $ . :-)
[quote]\P je oznaka za partitivni skup,samo što bi P trebalo biti 'pisano P',dakle _lijepo_ slovo P.[/quote]
A čuj... beauty is in the eye of beholder. :-P <- ne_lijepo P ;- ))
[quote]Imam bolju,intuivniju oznaku: JP[/quote]
Samo naprijed. Slobodno to koristi, razumjet ću. Hoće li i drugi, preostaje da vidiš. ;-)
[quote],gdje da se javim za prihvaćanje oznake kao službene u internet komunikaciji ? :wicked:[/quote]
Vidiš, to i mene zanima. :->
Uvijek možeš napraviti nešto poput http://web.math.hr/~veky/hsmath/Tm/mathscii.html . :-)
[quote]Ne upropastimo gledatelju rasplet filma prije nego je upoznao atmosferu istoga.
Tek sam sjeo u kinu i načeo kokice.;)[/quote]
Ma kakav rasplet... to je tek pravi zaplet. ;-)
[quote]A i već ovaj foršpan što si ga dao može u gledatelju izazvati mučninu zbog nadasve degutantno-šokatne scene u kojoj je broj 1 zapravo... :crazyeyes: :crazy: ...
to je kao,učenje matematike ispočetka,dođe ti profać i kaže:
-ok,dosad smo smatrali da je 1 samo jedan groš,čovjek,pas,oblak,duh,teorem...sve je to dio velike vladine urote zataškavanja i zato se primite čvrsto za sjedalice(mozgove):1 je zapravo skup što sadrži...[/quote]
Pa nije to ništa tako nekompatibilno. Razmišljanje može slobodno nastaviti ovako:
...No groš, čovjek i pas nisu math-objekti, i užasno su komplicirani za definiranje. Oblak je malo jednostavniji, ali i dalje zahtijeva da izađemo izvan math svijeta. Duh se uopće ne može suvislo definirati. :-) Teorem doduše ima math-definiciju, ali ona je dosta nezgodna za shvatiti na samom početku, i u svakom slučaju uključuje meta-logiku koju bismo bar u ovoj fazi htjeli izbjeći.
_Ali_, u svom tom razmišljanju što je broj 1 , vidjeli smo da je potpuno svejedno _što_ je objekt u pitanju, dok god je jedinstven i možemo ga promatrati odvojeno -- staviti u singleton, rekli bi mathematičari. Dakle, treba nam samo neki specijalni objekt kojeg je lako math-definirati, jedinstven je, i može biti element skupa. Još jedan zahtjev je da ne koristi broj 1 u svojoj definiciji (da ne dobijemo cirkularnost). :-)
Lako se vidi da prazan skup savršeno dobro zadovoljava sve zahtjeve. Dakle, prirodno je 1 definirati kao {0} . :-)
[quote][quote]Gr. Ajde, što bi po tvome bilo logičnije od toga? [/quote]
Ma dovoljno je ovo:
Iz pretpostavke da _govorim istinu_ ne mogu povući(izreći) nikakvu laž.
Slažem se.
Iz pretpostavke da _govorim laž_ mogu povući(izreći) nekakvu istinu.
Kako,ako ''lažem k'o pas'' ?[/quote]
Ne znam što ti znači "lažem k'o pas". Univerzalno lagati ionako nije moguće -- to pokazuje npr. Epimenidov paradoks ("Ova rečenica je lažna."). Dakle, tu i tamo ćeš definitivno izreći neku istinu. :-)
[quote](ova tvrdnja se dokazuje i bez zahtjevanja da je funkcija injekcija,ona vrijedi općenito za svaku funkciju)[/quote]
Točno, dakle nisi morao ponovo pisati (čak ni copy/pasteati : )cijeli dokaz. Sad nije toliko bitno, no nauči se da smiješ koristiti "već dokazano" kao napomenu u daljnjim dokazima. Kad kreneš u puno kompliciranije dokaze, to će postati esencijalno, da ne ideš svaki put sve do aksiomâ...
((Dokaz ok.))
[quote]Sviđa mi se ovaj način razmišljanja.[/quote]
I mislio sam da će ti se svidjeti. Note "mehanički" gore. ;-P
[quote]Smijem li vidjeti kako razmišljaš u situaciji:
vrijedi li jednakost,lijeva ili desna inkluzija?Između skupova:
f^>(X\Y) i f^>(X)\f^>(Y) .[/quote]
Kako ja razmišljam, vjerojatno ne želiš znati (pričali smo o tome). :-)
No ovaj stil razmišljanja možeš lijepo provesti i u ovom slučaju. Go ahead. (-:
[quote]Sorry ako ću djelovati iritantno ali nismo li negdje već rekli da je tvrdnja nešto već dokazano.
Nisi li htio reći da _hipoteza_ ne vrijedi :?: :?[/quote]
_Tvoja_ tvrdnja. Tvoje tvrdnje često ne vrijede. :-p
"Tvrdnja" u nematematičkom smislu, that is. "Tvrdnja" je valjda jedina riječ tog tipa koja se koristi i u svakodnevnogovornom kontekstu...
[quote]vidim da imaš novi sig,ne sviđa ti se ono što vidiš oko sebe...josh da gledaš telku tek bi vidio koliko je ta kost oglobana...[/quote]
Mislim da nisi shvatio. ;-) ButNeverMind...
| Vincent Van Ear (napisa): | | Citat: | | Pa sramoti te najvećim dijelom upravo zato što ga smatraš posebnim... :-/ |
Dobro,probat ću ga mentalno komercijalizirati bez obzira što je on _kolekcija ničega_ . |
Štogod. Da si bio na mojim vježbama, uvjeren sam da ne bi skupove smatrao kolekcijama. :→
| Citat: | Jelda ti ''fornije'' pisati ''normalno'' nego u toj skripti ?
Mislim,što te sprečava u pisanju skripte nego navika samog kuckanja bez nekih regula... |
Ovisi koliko ozbiljno shvatiš "regule". Jedino što me _zapravo_ nervira je pisanje [ latex ] i [/ latex ] tagova. Puno bih sretniji bio s jednostavnim $ $ . 
| Citat: | | \P je oznaka za partitivni skup,samo što bi P trebalo biti 'pisano P',dakle _lijepo_ slovo P. |
A čuj... beauty is in the eye of beholder.  ← ne_lijepo P ;- )) ← ne_lijepo P ;- ))
| Citat: | | Imam bolju,intuivniju oznaku: JP |
Samo naprijed. Slobodno to koristi, razumjet ću. Hoće li i drugi, preostaje da vidiš. 
| Citat: | ,gdje da se javim za prihvaćanje oznake kao službene u internet komunikaciji ?  |
Vidiš, to i mene zanima. :→
Uvijek možeš napraviti nešto poput http://web.math.hr/~veky/hsmath/Tm/mathscii.html . 
| Citat: | Ne upropastimo gledatelju rasplet filma prije nego je upoznao atmosferu istoga.
Tek sam sjeo u kinu i načeo kokice. |
Ma kakav rasplet... to je tek pravi zaplet. 
| Citat: | A i već ovaj foršpan što si ga dao može u gledatelju izazvati mučninu zbog nadasve degutantno-šokatne scene u kojoj je broj 1 zapravo...   ... ...
to je kao,učenje matematike ispočetka,dođe ti profać i kaže:
-ok,dosad smo smatrali da je 1 samo jedan groš,čovjek,pas,oblak,duh,teorem...sve je to dio velike vladine urote zataškavanja i zato se primite čvrsto za sjedalice(mozgove):1 je zapravo skup što sadrži... |
Pa nije to ništa tako nekompatibilno. Razmišljanje može slobodno nastaviti ovako:
...No groš, čovjek i pas nisu math-objekti, i užasno su komplicirani za definiranje. Oblak je malo jednostavniji, ali i dalje zahtijeva da izađemo izvan math svijeta. Duh se uopće ne može suvislo definirati.  Teorem doduše ima math-definiciju, ali ona je dosta nezgodna za shvatiti na samom početku, i u svakom slučaju uključuje meta-logiku koju bismo bar u ovoj fazi htjeli izbjeći. Teorem doduše ima math-definiciju, ali ona je dosta nezgodna za shvatiti na samom početku, i u svakom slučaju uključuje meta-logiku koju bismo bar u ovoj fazi htjeli izbjeći.
_Ali_, u svom tom razmišljanju što je broj 1 , vidjeli smo da je potpuno svejedno _što_ je objekt u pitanju, dok god je jedinstven i možemo ga promatrati odvojeno – staviti u singleton, rekli bi mathematičari. Dakle, treba nam samo neki specijalni objekt kojeg je lako math-definirati, jedinstven je, i može biti element skupa. Još jedan zahtjev je da ne koristi broj 1 u svojoj definiciji (da ne dobijemo cirkularnost). 
Lako se vidi da prazan skup savršeno dobro zadovoljava sve zahtjeve. Dakle, prirodno je 1 definirati kao {0} . 
| Citat: | | Citat: | | Gr. Ajde, što bi po tvome bilo logičnije od toga? |
Ma dovoljno je ovo:
Iz pretpostavke da _govorim istinu_ ne mogu povući(izreći) nikakvu laž.
Slažem se.
Iz pretpostavke da _govorim laž_ mogu povući(izreći) nekakvu istinu.
Kako,ako ''lažem k'o pas'' ? |
Ne znam što ti znači "lažem k'o pas". Univerzalno lagati ionako nije moguće – to pokazuje npr. Epimenidov paradoks ("Ova rečenica je lažna."). Dakle, tu i tamo ćeš definitivno izreći neku istinu. 
| Citat: | | (ova tvrdnja se dokazuje i bez zahtjevanja da je funkcija injekcija,ona vrijedi općenito za svaku funkciju) |
Točno, dakle nisi morao ponovo pisati (čak ni copy/pasteati : )cijeli dokaz. Sad nije toliko bitno, no nauči se da smiješ koristiti "već dokazano" kao napomenu u daljnjim dokazima. Kad kreneš u puno kompliciranije dokaze, to će postati esencijalno, da ne ideš svaki put sve do aksiomâ...
((Dokaz ok.))
| Citat: | | Sviđa mi se ovaj način razmišljanja. |
I mislio sam da će ti se svidjeti. Note "mehanički" gore. ;-P
| Citat: | Smijem li vidjeti kako razmišljaš u situaciji:
vrijedi li jednakost,lijeva ili desna inkluzija?Između skupova:
f^>(X\Y) i f^>(X)\f^>(Y) . |
Kako ja razmišljam, vjerojatno ne želiš znati (pričali smo o tome). 
No ovaj stil razmišljanja možeš lijepo provesti i u ovom slučaju. Go ahead. (-:
| Citat: | Sorry ako ću djelovati iritantno ali nismo li negdje već rekli da je tvrdnja nešto već dokazano.
Nisi li htio reći da _hipoteza_ ne vrijedi   |
_Tvoja_ tvrdnja. Tvoje tvrdnje često ne vrijede. :-p
"Tvrdnja" u nematematičkom smislu, that is. "Tvrdnja" je valjda jedina riječ tog tipa koja se koristi i u svakodnevnogovornom kontekstu...
| Citat: | | vidim da imaš novi sig,ne sviđa ti se ono što vidiš oko sebe...josh da gledaš telku tek bi vidio koliko je ta kost oglobana... |
Mislim da nisi shvatio.  ButNeverMind... ButNeverMind...
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
|






