| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 0:36 pet, 21. 1. 2005 Naslov: Limes iz kucnog uratka Postano: 0:36 pet, 21. 1. 2005 Naslov: Limes iz kucnog uratka |
    |
|
|
Ne, nije ga :bow: vsego zadao: samo sto je KU zesci nego DZ. 8)
Evo 17-og limesa od njih 100 iz KU:
[latex]\displaystyle\lim_{x\to +\infty}\left(x+\sqrt[3]{1-x^3}\right)[/latex]
Uglavnom, pokusao sam stosta...
Mnoziti raznovrsnim korjenjem, uvesti neku blesavu supstituciju i slicno.
Bude li ovaj rijesen, imat cu prvih 30. Hence, 70 to go. :D
(Samo recenica upute koja vodi rjesenju bit ce sasvim dovoljna. 8))
Ne, nije ga  vsego zadao: samo sto je KU zesci nego DZ. vsego zadao: samo sto je KU zesci nego DZ. 
Evo 17-og limesa od njih 100 iz KU:
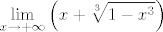
Uglavnom, pokusao sam stosta...
Mnoziti raznovrsnim korjenjem, uvesti neku blesavu supstituciju i slicno.
Bude li ovaj rijesen, imat cu prvih 30. Hence, 70 to go. 
(Samo recenica upute koja vodi rjesenju bit ce sasvim dovoljna.  ) )
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 16:17 sub, 22. 1. 2005 Naslov: Postano: 16:17 sub, 22. 1. 2005 Naslov: |
    |
|
|
Totalno nisam shvatio...
Prvo ne znam sto je 0_+ (ako si mislio na jednostrani limes, nismo ga jos primjenjivali), zatim ne kuzim o kojim kubovima se tu moze raditi (buduci je u zadatku korjenje).
Anyway, evo jos nekoliko zadataka za koje bih molio uputu:
33. [latex]\displaystyle\lim_{x\to \pi}\frac{\sin ax}{\sin bx}, a,b\in\mathbf{N}[/latex]
38. [latex]\displaystyle\lim_{x\to a}\frac{\sin x-\sin a}{x-a}, a\in\mathbf{R}[/latex]
46. [latex]\displaystyle\lim_{x\to \frac{\pi}{3}}\frac{\sin \left(x-\frac{\pi}{3}\right)}{1-2\cos x}[/latex]
49. [latex]\displaystyle\lim_{x\to 0}\frac{1+\sin x-\cos x}{1+\sin px-\cos px}, p\neq 0[/latex]
Dosao sam tocno do polovice (50/100) i zaista sam isprobao svasta na ovim zadacima, ali nista nije upalilo (45/50 i nije tako lose, ne? 8)).
Ako je moguce primijeniti trik iz nekog zadatka do tih, neka kaze tko zna. :D
Zahvaljujem. 8)
Totalno nisam shvatio...
Prvo ne znam sto je 0_+ (ako si mislio na jednostrani limes, nismo ga jos primjenjivali), zatim ne kuzim o kojim kubovima se tu moze raditi (buduci je u zadatku korjenje).
Anyway, evo jos nekoliko zadataka za koje bih molio uputu:
33. 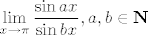
38. 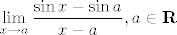
46. 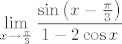
49. 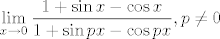
Dosao sam tocno do polovice (50/100) i zaista sam isprobao svasta na ovim zadacima, ali nista nije upalilo (45/50 i nije tako lose, ne?  ). ).
Ako je moguce primijeniti trik iz nekog zadatka do tih, neka kaze tko zna. 
Zahvaljujem. 
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 19:10 sub, 22. 1. 2005 Naslov: Postano: 19:10 sub, 22. 1. 2005 Naslov: |
    |
|
|
Ideees...
Vjekovac, nemam rijeci. :shock:
Hvala ti!!! 8)
E, da... Kolokvij u ponedjeljak...
1. Smijemo li na papiru s derivacijama i limesima imati i trig. identitete i adicijske teoreme?
Sto ako ne? Bubetati ih napamet zaista nema smisla, a izvodenje traje.
2. Kad znamo da moramo koristiti onaj teorem o sendvicu?
Naime, kod nas na vjezbama ga [b]uopce[/b] ne spominjemo (obradili ga jesmo, a primijenili najvise dvaput), pa ne bih htio opet zeznuti kao prosli put.
Ideees...
Vjekovac, nemam rijeci. 
Hvala ti!!! 
E, da... Kolokvij u ponedjeljak...
1. Smijemo li na papiru s derivacijama i limesima imati i trig. identitete i adicijske teoreme?
Sto ako ne? Bubetati ih napamet zaista nema smisla, a izvodenje traje.
2. Kad znamo da moramo koristiti onaj teorem o sendvicu?
Naime, kod nas na vjezbama ga uopce ne spominjemo (obradili ga jesmo, a primijenili najvise dvaput), pa ne bih htio opet zeznuti kao prosli put.
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 19:20 sub, 22. 1. 2005 Naslov: Postano: 19:20 sub, 22. 1. 2005 Naslov: |
    |
|
|
[quote="Smith"]Ideees...[/quote]
Ideeem... :)
Sad sam se sjetio da bi u 33. zadatku metodički bilo bolje da sam odmah supstituirao [latex]y=x-\pi[/latex]. Ovako možda izgleda da je kao neka strašna ideja oduzeti [latex]a\pi[/latex], odnosno [latex]b\pi[/latex], ali kad uvrstimo [latex]x=y+\pi[/latex] račun postaje sasvim logičan.
Općenito je najpametnije limes x->a svesti supstitucijom y=x-a na limes y->0.
-------------------
[quote="Smith"]1. Smijemo li na papiru s derivacijama i limesima imati i trig. identitete i adicijske teoreme?[/quote]
Ma dozvoljene su bilo kakve formule (samo da nisu riješeni zadaci). Najbolje sve na jednom papiru da ne bi pobudile sumnju asistenta koji čuva.
[quote="Smith"]2. Kad znamo da moramo koristiti onaj teorem o sendvicu? [/quote]
Pitanje nema smisla?! Ne moramo ga koristiti ako znamo zadatak riješiti bez njegove primjene.
Na 2. kolokviju je bio zadatak koji se najprirodnije mogao riješiti primjenom [i]sendviča[/i].
Nakon dijeljenja trebalo je dokazati ovako nešto:
[latex]\lim_{n\to\infty}\left(\frac{6}{10+3\cos(n^{10})}\right)^{n}=0[/latex]
Ako hoćeš, ti to možeš pokazati i npr. po definiciji, ali najlakše je da se odozgo ocijeni s (6/7)^n pa primijeni tm o sendviču.
Ja sam bio strog jer nisam davao sve bodove za heurističke argumente (pa ovo [i]brže raste [/i]i sl.), ali nisam inzistirao na teoremu o sendviču.
| Smith (napisa): | | Ideees... |
Ideeem... 
Sad sam se sjetio da bi u 33. zadatku metodički bilo bolje da sam odmah supstituirao 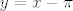 . Ovako možda izgleda da je kao neka strašna ideja oduzeti . Ovako možda izgleda da je kao neka strašna ideja oduzeti 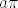 , odnosno , odnosno 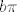 , ali kad uvrstimo , ali kad uvrstimo 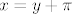 račun postaje sasvim logičan. račun postaje sasvim logičan.
Općenito je najpametnije limes x→a svesti supstitucijom y=x-a na limes y→0.
-------------------
| Smith (napisa): | | 1. Smijemo li na papiru s derivacijama i limesima imati i trig. identitete i adicijske teoreme? |
Ma dozvoljene su bilo kakve formule (samo da nisu riješeni zadaci). Najbolje sve na jednom papiru da ne bi pobudile sumnju asistenta koji čuva.
| Smith (napisa): | | 2. Kad znamo da moramo koristiti onaj teorem o sendvicu? |
Pitanje nema smisla?! Ne moramo ga koristiti ako znamo zadatak riješiti bez njegove primjene.
Na 2. kolokviju je bio zadatak koji se najprirodnije mogao riješiti primjenom sendviča.
Nakon dijeljenja trebalo je dokazati ovako nešto:
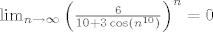
Ako hoćeš, ti to možeš pokazati i npr. po definiciji, ali najlakše je da se odozgo ocijeni s (6/7)^n pa primijeni tm o sendviču.
Ja sam bio strog jer nisam davao sve bodove za heurističke argumente (pa ovo brže raste i sl.), ali nisam inzistirao na teoremu o sendviču.
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
 Postano: 19:57 sub, 22. 1. 2005 Naslov: Postano: 19:57 sub, 22. 1. 2005 Naslov: |
    |
|
|
[quote="vjekovac"]
Sad sam se sjetio...[/quote]
Nema frke, odmah sam to bio skuzio i odmah supstituirao. 8)
[quote]Općenito je najpametnije limes x->a svesti supstitucijom y=x-a na limes y->0.[/quote]
Odlicno, ovo uvelike pomaze...
[quote]Ma dozvoljene su bilo kakve formule (samo da nisu riješeni zadaci).[/quote]
...a o ovome da ne pricam. :D
[quote]Najbolje sve na jednom papiru da ne bi pobudile sumnju asistenta koji čuva.[/quote]
Okej.
[quote]Pitanje nema smisla?! Ne moramo ga koristiti ako znamo zadatak riješiti bez njegove primjene.[/quote]
Ok.
[quote]Na 2. kolokviju je bio zadatak koji se najprirodnije mogao riješiti primjenom [i]sendviča[/i].
Nakon dijeljenja trebalo je dokazati ovako nešto:
[latex]\lim_{n\to\infty}\left(\frac{6}{10+3\cos(n^{10})}\right)^{n}=0[/latex]
Ako hoćeš, ti to možeš pokazati i npr. po definiciji, ali najlakše je da se odozgo ocijeni s (6/7)^n pa primijeni tm o sendviču.[/quote]
Aaa... Jasno.
[quote]Ja sam bio strog jer nisam davao sve bodove za heurističke argumente (pa ovo [i]brže raste [/i]i sl.), ali nisam inzistirao na teoremu o sendviču.[/quote]
Kuzim, kuzim.
Nije to bilo strogo, sve ok. Jasno mi je gdje sam fulao. 8)
Jos jednom, zaista ti puno hvala na odgovorima. :wink:
| vjekovac (napisa): |
Sad sam se sjetio... |
Nema frke, odmah sam to bio skuzio i odmah supstituirao. 
| Citat: | | Općenito je najpametnije limes x->a svesti supstitucijom y=x-a na limes y->0. |
Odlicno, ovo uvelike pomaze...
| Citat: | | Ma dozvoljene su bilo kakve formule (samo da nisu riješeni zadaci). |
...a o ovome da ne pricam. 
| Citat: | | Najbolje sve na jednom papiru da ne bi pobudile sumnju asistenta koji čuva. |
Okej.
| Citat: | | Pitanje nema smisla?! Ne moramo ga koristiti ako znamo zadatak riješiti bez njegove primjene. |
Ok.
| Citat: | Na 2. kolokviju je bio zadatak koji se najprirodnije mogao riješiti primjenom sendviča.
Nakon dijeljenja trebalo je dokazati ovako nešto:
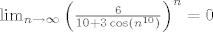
Ako hoćeš, ti to možeš pokazati i npr. po definiciji, ali najlakše je da se odozgo ocijeni s (6/7)^n pa primijeni tm o sendviču. |
Aaa... Jasno.
| Citat: | | Ja sam bio strog jer nisam davao sve bodove za heurističke argumente (pa ovo brže raste i sl.), ali nisam inzistirao na teoremu o sendviču. |
Kuzim, kuzim.
Nije to bilo strogo, sve ok. Jasno mi je gdje sam fulao. 
Jos jednom, zaista ti puno hvala na odgovorima. 
_________________
We only have one candle
To burn down to the handle...
- Sonata Arctica, Weballergy
|
|
| [Vrh] |
|
|











