|
1. zadatak:
Promatramo skup
[latex]
A=\{(x,y,z)\in [0,1]^3\colon xyz\leq\frac{1}{2}\}.
[/latex]
Lakše je izračunati volumen skupa [latex]A^c[/latex]:
[latex]
\lambda(A^c)={\int\int\int}_{A^c}\,\,dz\,dy\,dx=\int_0^1 \int_{\frac{1}{2x}}^1 \int_{\frac{1}{2xy}}^1 dz\,dy\,dx=
\int_0^1 \int_{\frac{1}{2x}}^1 (1-\frac{1}{2xy})\,dy\,dx=...
[/latex]
gdje je [latex]\lambda[/latex] u ovom slučaju volumen skupa.
Tada je vjerojatnost da točka upadne u skup [latex]A[/latex]
[latex]\frac{\lambda(A)}{\lambda([0,1]^3)}[/latex]
2. zadatrak:
Zbog [latex]x,y,z\in[0,1][/latex] uvjet je
[latex]
z\leq\sqrt{xy}
[/latex]
Stavimo
[latex]
A=\{(x,y,z)\in [0,1]^3\colon z\leq \sqrt{xy}\}
[/latex]
Ako definiramo
[latex]
f:[0,1]\times [0,1] \rightarrow \mathrm{R}\\
f(x,y)=\sqrt{xy},
[/latex]
onda je volumen skupa A zapravo volumen ispod grafa funkcije f, pa je
[latex]
\lambda(A)=\int_0^1 \int_0^1 f(x,y)\,dx\,dy=\int_0^1\,\int_0^1 \sqrt{xy}\,dx\,dy=...
[/latex]
3. zadatak:
Nisam siguran, ali možda ovako:
Biramo:
[latex]
(x,y)\in [0,10]^2 \mbox{ takve da je } x\geq 2, y\geq 2, x+y\leq 8
[/latex]
Nacrtaj to u ravnini i izračunaj površinu...
1. zadatak:
Promatramo skup
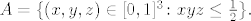
Lakše je izračunati volumen skupa 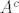 : :
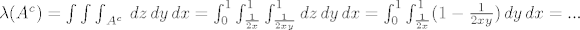
gdje je  u ovom slučaju volumen skupa. u ovom slučaju volumen skupa.
Tada je vjerojatnost da točka upadne u skup 
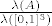
2. zadatrak:
Zbog 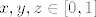 uvjet je uvjet je
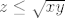
Stavimo
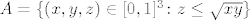
Ako definiramo
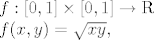
onda je volumen skupa A zapravo volumen ispod grafa funkcije f, pa je
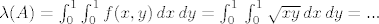
3. zadatak:
Nisam siguran, ali možda ovako:
Biramo:

Nacrtaj to u ravnini i izračunaj površinu...
|





