| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Pero_
Gost
|
|
| [Vrh] |
|
Marijan
Gost
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Pero_
Gost
|
|
| [Vrh] |
|
defar
Forumaš(ica)


Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
 Postano: 20:19 čet, 3. 2. 2005 Naslov: Postano: 20:19 čet, 3. 2. 2005 Naslov: |
    |
|
|
a sto se prvog b) dijela tice, koliko ima uredjenih k-torki (S_1, ...S_k) podskupova n-clanog skupa S za koje vrijedi S_1nS_2...nS_k=0
, jel' ovo tocno:
(S_1, ...S_k) <--> [s_i,j] E M_nk({0,1})
sad, one koje zelimo prebrojiti su takvi da u svakom redu od [s_i,j] postoji bar jedna nula, a takovih ima:
((1+1)^k - 1)^n = (2^k-1)^n (za svaki red se bira mjesto za 1 nulu, ili za dvije nule...ili za k nula)?
P.S. zao mi, krcko, sto si morao i to od mojeg uradka ispravljat :cry: no, bice bolje drugi put :D stvarno cu se skulirat 8)
a sto se prvog b) dijela tice, koliko ima uredjenih k-torki (S_1, ...S_k) podskupova n-clanog skupa S za koje vrijedi S_1nS_2...nS_k=0
, jel' ovo tocno:
(S_1, ...S_k) ↔ [s_i,j] E M_nk({0,1})
sad, one koje zelimo prebrojiti su takvi da u svakom redu od [s_i,j] postoji bar jedna nula, a takovih ima:
((1+1)^k - 1)^n = (2^k-1)^n (za svaki red se bira mjesto za 1 nulu, ili za dvije nule...ili za k nula)?
P.S. zao mi, krcko, sto si morao i to od mojeg uradka ispravljat  no, bice bolje drugi put no, bice bolje drugi put  stvarno cu se skulirat stvarno cu se skulirat 
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Marijan
Gost
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 12:56 pet, 4. 2. 2005 Naslov: Postano: 12:56 pet, 4. 2. 2005 Naslov: |
    |
|
|
Rjesenje prvog (a) je (k+1)^n.
U cetvrtom EFI je [latex](1+x){e^x+e^{-x}\over 2}(e^x-1)e^x[/latex]. Za n>=2 koeficijent uz x^n pomnozen s n! je [latex]{1\over 2}\left( 3^n-2^n+1+n(3^{n-1}-2^{n-1}+1)\right)[/latex].
U petom je trebalo konstruirati bijekciju izmedju trokuta a+b+c=n i particija 2x+3y+4z=n-3. Veza je x=b-c, y=b+c-a-1, z=a-b. Ideja je transponirati Ferrerov dijagram particije a+b+c=n koja zadovoljava nejednakost trokuta. Dobije se particija od n u dijelove 1, 2, 3 uz dodatni uvijet, a to se uz malo prtljanja moze svesti na particiju od n-3 u dijelove 2, 3, 4 bez dodatnih uvjeta. Ovo je bio najtezi zadatak.
Detaljno raspisana rjesenja mozete dobiti od mene. Stavio sam na oglasnu plocu, no vjerujem da je u medjuvremenu nestalo (mozda imaju kopiju u skriptarnici).
Rjesenje prvog (a) je (k+1)^n.
U cetvrtom EFI je 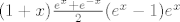 . Za n>=2 koeficijent uz x^n pomnozen s n! je . Za n>=2 koeficijent uz x^n pomnozen s n! je 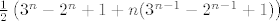 . .
U petom je trebalo konstruirati bijekciju izmedju trokuta a+b+c=n i particija 2x+3y+4z=n-3. Veza je x=b-c, y=b+c-a-1, z=a-b. Ideja je transponirati Ferrerov dijagram particije a+b+c=n koja zadovoljava nejednakost trokuta. Dobije se particija od n u dijelove 1, 2, 3 uz dodatni uvijet, a to se uz malo prtljanja moze svesti na particiju od n-3 u dijelove 2, 3, 4 bez dodatnih uvjeta. Ovo je bio najtezi zadatak.
Detaljno raspisana rjesenja mozete dobiti od mene. Stavio sam na oglasnu plocu, no vjerujem da je u medjuvremenu nestalo (mozda imaju kopiju u skriptarnici).
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
|




