| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 1:17 ned, 6. 2. 2005 Naslov: zadatak s vježbi Postano: 1:17 ned, 6. 2. 2005 Naslov: zadatak s vježbi |
    |
|
|
Kako glasi jedn. ravnine u E3 koja sadrži točke E3, T=(3,0,0) i sa ravninom x-y zatvara kut od 60°.
U rjesenju zadatka se pretpostavi da je //n//=1 (n=normala traženog pravca) i kaže se da je normala ravnine x-y =(0,0,1).
Može li mi netko objasniti kako se dodje do tih normala?[/list][/u]
Kako glasi jedn. ravnine u E3 koja sadrži točke E3, T=(3,0,0) i sa ravninom x-y zatvara kut od 60°.
U rjesenju zadatka se pretpostavi da je //n//=1 (n=normala traženog pravca) i kaže se da je normala ravnine x-y =(0,0,1).
Može li mi netko objasniti kako se dodje do tih normala?[/list][/u]
|
|
| [Vrh] |
|
Gost
|
 Postano: 2:32 ned, 6. 2. 2005 Naslov: Postano: 2:32 ned, 6. 2. 2005 Naslov: |
    |
|
|
Nesto u formulaciji zadatka nije dobro. Za ravninu Ax+By+Cz+D=0 vektor normale je (A,B,C), a za normiranje treba podijeliti s normom tog vektora. Zato je vektor normale zadane ravnine jednak (1,-1,0), a s vektorom normale trazene ravnine treba zatvarati kut od 60o tako d aje skalarni produkt s jedne strane jednak A-B, a s druge sqrt(2)/2 ako uzmemo da je trazena ravnina Ax+By+Cz+D =0 i da je vektor normale jedinicni. Tu jednadzbu mora ispunjavati svaka tocka ravnine, dakle i (3,0,0) pa je 3A+D = 0 i jos je A^2+B^2+C^2 = 1. Nije mi jasan jos jedan podatak o trazenoj ravnini, sto jos sadrzi (ono "tocke E3")?
Nesto u formulaciji zadatka nije dobro. Za ravninu Ax+By+Cz+D=0 vektor normale je (A,B,C), a za normiranje treba podijeliti s normom tog vektora. Zato je vektor normale zadane ravnine jednak (1,-1,0), a s vektorom normale trazene ravnine treba zatvarati kut od 60o tako d aje skalarni produkt s jedne strane jednak A-B, a s druge sqrt(2)/2 ako uzmemo da je trazena ravnina Ax+By+Cz+D =0 i da je vektor normale jedinicni. Tu jednadzbu mora ispunjavati svaka tocka ravnine, dakle i (3,0,0) pa je 3A+D = 0 i jos je A^2+B^2+C^2 = 1. Nije mi jasan jos jedan podatak o trazenoj ravnini, sto jos sadrzi (ono "tocke E3")?
|
|
| [Vrh] |
|
mea
Forumaš(ica)

Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
|
 Postano: 1:29 pon, 7. 2. 2005 Naslov: Postano: 1:29 pon, 7. 2. 2005 Naslov: |
    |
|
|
[quote="Anonymous"]Zato je vektor normale zadane ravnine jednak (1,-1,0)...[/quote]
Ne... ne... ne... Ne x-y=nešto. Nego xy-ravnina.
To je ravnina u kojoj su x i y koordinate točaka bilo kakve (OK, realne), a treća, z koordinata je jednaka nuli. Dakle, jednadžba te ravnine je z=0.
Dalje zaključujte sami.
[quote="Anonymous"]Nije mi jasan jos jedan podatak o trazenoj ravnini, sto jos sadrzi (ono "tocke E3")?[/quote]
[latex]E_3=(0,0,1)[/latex]
Mea
| Anonymous (napisa): | | Zato je vektor normale zadane ravnine jednak (1,-1,0)... |
Ne... ne... ne... Ne x-y=nešto. Nego xy-ravnina.
To je ravnina u kojoj su x i y koordinate točaka bilo kakve (OK, realne), a treća, z koordinata je jednaka nuli. Dakle, jednadžba te ravnine je z=0.
Dalje zaključujte sami.
| Anonymous (napisa): | | Nije mi jasan jos jedan podatak o trazenoj ravnini, sto jos sadrzi (ono "tocke E3")? |
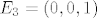
Mea
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mea
Forumaš(ica)

Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
|
|
| [Vrh] |
|
|



