| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 21:55 ned, 6. 2. 2005 Naslov: Postano: 21:55 ned, 6. 2. 2005 Naslov: |
    |
|
|
ajdemo konkretno jer ne kuzim kaj zelis reci.
zadatak ide ovako:
U unitarnom kompleksnom prostoru [latex]C^3[/latex] razapet je prostor [latex] L[/latex] vektorima [latex]a_1=(i, i, 1)[/latex] i [latex]a_2=(1,1,1)[/latex]. Odredite [latex]L*[/latex], te prikazite vektor [latex]b=(-1,1,-i+1)[/latex] kao sumu [latex]b=a+c[/latex] gdje je [latex]a\in L, c \in L*[/latex].
kako definirati skalarni produkt?
ajdemo konkretno jer ne kuzim kaj zelis reci.
zadatak ide ovako:
U unitarnom kompleksnom prostoru 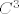 razapet je prostor razapet je prostor 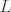 vektorima vektorima 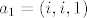 i i 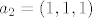 . Odredite . Odredite 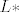 , te prikazite vektor , te prikazite vektor 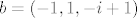 kao sumu kao sumu 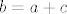 gdje je gdje je 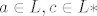 . .
kako definirati skalarni produkt?
|
|
| [Vrh] |
|
Gost
|
 Postano: 22:03 ned, 6. 2. 2005 Naslov: Postano: 22:03 ned, 6. 2. 2005 Naslov: |
    |
|
|
Evo ti primjer.
Unitarni prostor C^3 sa standardnim skalarnim produktom:
Neka su zadani vektori u=(1,i,1+i), v=(1-i, i, 2-i).
Skalarni produkt (u,v) = 1*(1+i) + i*(-i) + (1+i)*(2+i) itd, sad se dalje normalno racuna s kompleksnim brojevima. primijeti da su kod mnozenja odgovarajuih koordinata one od vektora v _kompleksno konjugirane_!
Evo ti primjer.
Unitarni prostor C^3 sa standardnim skalarnim produktom:
Neka su zadani vektori u=(1,i,1+i), v=(1-i, i, 2-i).
Skalarni produkt (u,v) = 1*(1+i) + i*(-i) + (1+i)*(2+i) itd, sad se dalje normalno racuna s kompleksnim brojevima. primijeti da su kod mnozenja odgovarajuih koordinata one od vektora v _kompleksno konjugirane_!
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 22:10 ned, 6. 2. 2005 Naslov: Re: Standardni skalarni produkt Postano: 22:10 ned, 6. 2. 2005 Naslov: Re: Standardni skalarni produkt |
    |
|
|
[quote="HijenA"]koji je standardni skalarni produkt nad kompleksnim prostorima?
ako su [latex]u, v \in\ R^3[/latex] (uzeo kao primjer dimenziju 3),
onda je skalarni produkt definiran:
[latex]<u|v>=x_1*y_1+x_2*y_2+x_3*y_3[/latex]
kako se definira nad kompleksnim prostorima? isto kao i kod realnih prostora, ili ima nekakva varijacija na temu?[/quote]
Ima varijacija na temu. (x|y):=x1*y1^conj+x2*y2^conj+x3*y3^conj , gdje je s yi^conj označen kompleksno konjugirani broj broju yi . Na primjer, ((0,2i,-5)|(2+i,i,3))=0*(2-i)+2i*(-i)+(-5)*3=2-15=-13 .
1. napomena: Da nije tako definiran, već direktno kao suma umnožaka koordinata, ne bi vrijedio aksiom pozitivnosti -- na primjer, u |C^2 , vektor (1,i) bi bio ortogonalan na samog sebe (efektivno norme nula), a vektor (i,0) bi na kvadrat davao -1 .
2. napomena: to možeš gledati i kao općeniti skalarni produkt, i u realnim prostorima -- samo što je x^conj=x za x@|R .
| HijenA (napisa): | koji je standardni skalarni produkt nad kompleksnim prostorima?
ako su 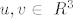 (uzeo kao primjer dimenziju 3), (uzeo kao primjer dimenziju 3),
onda je skalarni produkt definiran:
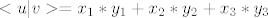
kako se definira nad kompleksnim prostorima? isto kao i kod realnih prostora, ili ima nekakva varijacija na temu? |
Ima varijacija na temu. (x|y):=x1*y1^conj+x2*y2^conj+x3*y3^conj , gdje je s yi^conj označen kompleksno konjugirani broj broju yi . Na primjer, ((0,2i,-5)|(2+i,i,3))=0*(2-i)+2i*(-i)+(-5)*3=2-15=-13 .
1. napomena: Da nije tako definiran, već direktno kao suma umnožaka koordinata, ne bi vrijedio aksiom pozitivnosti – na primjer, u |C^2 , vektor (1,i) bi bio ortogonalan na samog sebe (efektivno norme nula), a vektor (i,0) bi na kvadrat davao -1 .
2. napomena: to možeš gledati i kao općeniti skalarni produkt, i u realnim prostorima – samo što je x^conj=x za x@|R .
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
|








