| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 19:15 sri, 9. 2. 2005 Naslov: Re: Alef0 i Alef1 Postano: 19:15 sri, 9. 2. 2005 Naslov: Re: Alef0 i Alef1 |
    |
|
|
[quote="HijenA"]ali sto predstavlja [latex]\aleph_1[/latex]? ako je to prvi veci beskonacni kardinal od [latex]\aleph_0[/latex] da li on predstavlja kardinalni broj skupa |R ili nekog drugog skupa (bilo prebrojivog, bilo neprebrojivog)?[/quote]
Da. Recimo, kardinalni broj skupa svih prebrojivih ordinalâ. Baš kao što je alef0 kardinalni broj skupa svih konačnih ordinala -- jedino što se konačni ordinali zovu i ljepše: prirodni brojevi.
Konkretno, to je naravno neprebrojiv skup. alef1 ne može biti kardinalni broj nijednog prebrojivog skupa, jer je po definiciji _veći_ od alef1 .
HTH,
| HijenA (napisa): | ali sto predstavlja 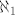 ? ako je to prvi veci beskonacni kardinal od ? ako je to prvi veci beskonacni kardinal od 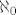 da li on predstavlja kardinalni broj skupa |R ili nekog drugog skupa (bilo prebrojivog, bilo neprebrojivog)? da li on predstavlja kardinalni broj skupa |R ili nekog drugog skupa (bilo prebrojivog, bilo neprebrojivog)? |
Da. Recimo, kardinalni broj skupa svih prebrojivih ordinalâ. Baš kao što je alef0 kardinalni broj skupa svih konačnih ordinala – jedino što se konačni ordinali zovu i ljepše: prirodni brojevi.
Konkretno, to je naravno neprebrojiv skup. alef1 ne može biti kardinalni broj nijednog prebrojivog skupa, jer je po definiciji _veći_ od alef1 .
HTH,
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 21:46 sri, 9. 2. 2005 Naslov: Re: Alef0 i Alef1 Postano: 21:46 sri, 9. 2. 2005 Naslov: Re: Alef0 i Alef1 |
    |
|
|
[quote="mdoko"][quote="HijenA"]
ali sto predstavlja [latex]\aleph_1[/latex]?
ako je to prvi veci beskonacni kardinal od [latex]\aleph_0[/latex] da li on predstavlja kardinalni broj skupa |R ili nekog drugog skupa (bilo prebrojivog, bilo neprebrojivog)?[/quote]
Kako sto predstavlja? Pa prvi kardinalni broj veci od [latex]\aleph_0[/latex]. Takav postoji po aksiomu dobre utemeljenosti.[/quote]
kakav je to broj? mislim...ako za neki skup kazem da mu je [latex]\aleph_1[/latex] kardinalni broj, sto sam rekao? nadam se da sad kuzis.
[quote]
Trebalo bi imati na umu da ne mozes reci da je [latex]\aleph_1[/latex] kardinalni broj skupa realnih brojeva. To je tzv. hipoteza kontinuuma za koju je dokazano da je nezavisna s aksimomima ZFC.[/quote]
a kako objasnjavas ovo sto je veky napisao post ispod? i sto znaci [i]hipoteza kontinuuma[/i]? mozes pojasnit taj izraz? i, ak ti se da, koji su osnovni aksiomi ZFC? i sto uopce ZFC znaci? :) znam da puno trazim, ali to me strasno interesira.
[quote]P.S. Zasto je ovo pod teorijom brojeva? Ne bi li bilo bolje ovo strpati pod teoriju skupova?[/quote]
ne znam...mislio sam, isprva, da razgovaramo o brojevima no ispalo je da razgovaramo o skupovima. bum PMal vsegu pa ce on prebacit raspravu na Teoriju skupova :)
| mdoko (napisa): | | HijenA (napisa): |
ali sto predstavlja 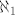 ? ?
ako je to prvi veci beskonacni kardinal od 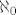 da li on predstavlja kardinalni broj skupa |R ili nekog drugog skupa (bilo prebrojivog, bilo neprebrojivog)? da li on predstavlja kardinalni broj skupa |R ili nekog drugog skupa (bilo prebrojivog, bilo neprebrojivog)? |
Kako sto predstavlja? Pa prvi kardinalni broj veci od 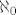 . Takav postoji po aksiomu dobre utemeljenosti. . Takav postoji po aksiomu dobre utemeljenosti. |
kakav je to broj? mislim...ako za neki skup kazem da mu je 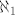 kardinalni broj, sto sam rekao? nadam se da sad kuzis. kardinalni broj, sto sam rekao? nadam se da sad kuzis.
| Citat: |
Trebalo bi imati na umu da ne mozes reci da je 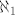 kardinalni broj skupa realnih brojeva. To je tzv. hipoteza kontinuuma za koju je dokazano da je nezavisna s aksimomima ZFC. kardinalni broj skupa realnih brojeva. To je tzv. hipoteza kontinuuma za koju je dokazano da je nezavisna s aksimomima ZFC. |
a kako objasnjavas ovo sto je veky napisao post ispod? i sto znaci hipoteza kontinuuma? mozes pojasnit taj izraz? i, ak ti se da, koji su osnovni aksiomi ZFC? i sto uopce ZFC znaci?  znam da puno trazim, ali to me strasno interesira. znam da puno trazim, ali to me strasno interesira.
| Citat: | | P.S. Zasto je ovo pod teorijom brojeva? Ne bi li bilo bolje ovo strpati pod teoriju skupova? |
ne znam...mislio sam, isprva, da razgovaramo o brojevima no ispalo je da razgovaramo o skupovima. bum PMal vsegu pa ce on prebacit raspravu na Teoriju skupova 
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 23:34 sri, 9. 2. 2005 Naslov: Re: Alef0 i Alef1 Postano: 23:34 sri, 9. 2. 2005 Naslov: Re: Alef0 i Alef1 |
    |
|
|
[quote="HijenA"]kakav je to broj?[/quote]
Hm. Kakav je broj 6.723 ? (vjekovac, nisam tebe pitao! ; )
Što misliš pod "kakav"? Na primjer, neprebrojiv je.
[quote] mislim...ako za neki skup kazem da mu je [latex]\aleph_1[/latex] kardinalni broj, sto sam rekao?[/quote]
(*1) Ako kažeš da je cardX=alef1 , rekao si da je X neprebrojiv skup, i da su svi podskupovi od X ili ekvipotentni s X , ili prebrojivi (tu pod prebrojivim mislim na konačne).
(*2) Baš kao što bi s cardX=alef0 rekao da je X beskonačan, i da su svi podskupovi od X ili ekvipotentni s X , ili konačni.
Ok?
[quote]i sto znaci [i]hipoteza kontinuuma[/i]? mozes pojasnit taj izraz?[/quote]
Hipoteza kontinuuma je da, kao što za primjer skupa kardinaliteta alef0 (najmanjeg beskonačnog skupa) imamo |N , tako bi primjer skupa kardinaliteta alef1 , najmanjeg _neprebrojivog_ skupa, bio |R .
[quote] i, ak ti se da, koji su osnovni aksiomi ZFC?[/quote]
http://planetmath.org/encyclopedia/ZermeloFraenkelAxioms.html
[quote] i sto uopce ZFC znaci? :)[/quote]
Zermelo-Fraenkel theory with Choice. Teorija u kojoj se bar principijelo može raditi više od 99% dosadašnje matematike.
[quote] znam da puno trazim, ali to me strasno interesira. [/quote]
Postoji Google. A uvijek možeš i mene uloviti na faksu. :-)
[quote]ne znam...mislio sam, isprva, da razgovaramo o brojevima no ispalo je da razgovaramo o skupovima.[/quote]
Hmm... pa brojevi su samo posebni skupovi. :-) Teorija skupova se dobrim dijelom bavi brojevima -- kardinalnim i ordinalnim. Teorija brojeva, OTOH, se uglavnom bavi samo _konačnim_ brojevima -- ovima manjima od alef0 . :-)
| HijenA (napisa): | | kakav je to broj? |
Hm. Kakav je broj 6.723 ? (vjekovac, nisam tebe pitao! ; )
Što misliš pod "kakav"? Na primjer, neprebrojiv je.
| Citat: | mislim...ako za neki skup kazem da mu je 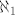 kardinalni broj, sto sam rekao? kardinalni broj, sto sam rekao? |
(*1) Ako kažeš da je cardX=alef1 , rekao si da je X neprebrojiv skup, i da su svi podskupovi od X ili ekvipotentni s X , ili prebrojivi (tu pod prebrojivim mislim na konačne).
(*2) Baš kao što bi s cardX=alef0 rekao da je X beskonačan, i da su svi podskupovi od X ili ekvipotentni s X , ili konačni.
Ok?
| Citat: | | i sto znaci hipoteza kontinuuma? mozes pojasnit taj izraz? |
Hipoteza kontinuuma je da, kao što za primjer skupa kardinaliteta alef0 (najmanjeg beskonačnog skupa) imamo |N , tako bi primjer skupa kardinaliteta alef1 , najmanjeg _neprebrojivog_ skupa, bio |R .
| Citat: | | i, ak ti se da, koji su osnovni aksiomi ZFC? |
http://planetmath.org/encyclopedia/ZermeloFraenkelAxioms.html
| Citat: | i sto uopce ZFC znaci?  |
Zermelo-Fraenkel theory with Choice. Teorija u kojoj se bar principijelo može raditi više od 99% dosadašnje matematike.
| Citat: | | znam da puno trazim, ali to me strasno interesira. |
Postoji Google. A uvijek možeš i mene uloviti na faksu. 
| Citat: | | ne znam...mislio sam, isprva, da razgovaramo o brojevima no ispalo je da razgovaramo o skupovima. |
Hmm... pa brojevi su samo posebni skupovi.  Teorija skupova se dobrim dijelom bavi brojevima – kardinalnim i ordinalnim. Teorija brojeva, OTOH, se uglavnom bavi samo _konačnim_ brojevima – ovima manjima od alef0 . Teorija skupova se dobrim dijelom bavi brojevima – kardinalnim i ordinalnim. Teorija brojeva, OTOH, se uglavnom bavi samo _konačnim_ brojevima – ovima manjima od alef0 . 
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 0:14 čet, 10. 2. 2005 Naslov: Re: Alef0 i Alef1 Postano: 0:14 čet, 10. 2. 2005 Naslov: Re: Alef0 i Alef1 |
    |
|
|
[quote="veky"][quote="HijenA"]kakav je to broj?[/quote]
Hm. Kakav je broj 6.723 ? (vjekovac, nisam tebe pitao! ; )[/quote]
decimalan :rotfl: ;-)
[quote]
Što misliš pod "kakav"? Na primjer, neprebrojiv je.
(*1) Ako kažeš da je cardX=alef1 , rekao si da je X neprebrojiv skup, i da su svi podskupovi od X ili ekvipotentni s X , ili prebrojivi (tu pod prebrojivim mislim na konačne).[/quote]
kad kazes ekvipotentni s X, onda mislis da imaju ista svojstva kao X (isti kardinalitet, prebrojivost/neprebrojivost i slicno)?
[quote]
(*2) Baš kao što bi s cardX=alef0 rekao da je X beskonačan, i da su svi podskupovi od X ili ekvipotentni s X , ili konačni.
Ok?[/quote]
ok...mislim da sam shvatio :D
[quote]
[quote]i sto znaci [i]hipoteza kontinuuma[/i]? mozes pojasnit taj izraz?[/quote]
Hipoteza kontinuuma je da, kao što za primjer skupa kardinaliteta alef0 (najmanjeg beskonačnog skupa) imamo |N , tako bi primjer skupa kardinaliteta alef1 , najmanjeg _neprebrojivog_ skupa, bio |R .[/quote]
still don't get it. mislim da si me vise zbunio nego sto sam bio zbunjen :?
[quote]
[quote] i, ak ti se da, koji su osnovni aksiomi ZFC?[/quote]
http://planetmath.org/encyclopedia/ZermeloFraenkelAxioms.html[/quote]
zahvaljujem na linku...nismo li mi vecinu tih aksioma radili iz elementarne? samo ih nismo tako zvali :)
[quote]
[quote] i sto uopce ZFC znaci? :)[/quote]
Zermelo-Fraenkel theory with Choice. Teorija u kojoj se bar principijelo može raditi više od 99% dosadašnje matematike.[/quote]
again, zahvaljujem na objasnjenju :D
[quote]
[quote] znam da puno trazim, ali to me strasno interesira. [/quote]
Postoji Google. A uvijek možeš i mene uloviti na faksu. :-)[/quote]
ma znam da postoji google. inace bi se njemu prvi obratio. medjutim, kad sam trazio onaj skalarni produkt nad kompleksnim prostorima, nasao sam sve osim toga. besides, mislim da je ovo konkretno pitanje koje potpuno, i po svemu, spada na ovaj forum...mozda ne na UTB, ali u TS sigurno :)
[quote]
[quote]ne znam...mislio sam, isprva, da razgovaramo o brojevima no ispalo je da razgovaramo o skupovima.[/quote]
Hmm... pa brojevi su samo posebni skupovi. :-) Teorija skupova se dobrim dijelom bavi brojevima -- kardinalnim i ordinalnim. Teorija brojeva, OTOH, se uglavnom bavi samo _konačnim_ brojevima -- ovima manjima od alef0 . :-)[/quote]
da...skuzio sam. zapravo...mene malo muce i definicije nekih, pa mogao bi reci, osnovnih pojmova. recimo...sto je to kardinalni broj?
po [url=http://mathworld.wolfram.com/CardinalNumber.html]Mathworldu[/url]
[quote="Mathworld"]
One of the first serious mathematical definitions of cardinal was the one devised by Gottlob Frege and Bertrand Russell, who defined a cardinal number as the set of all sets equipollent to A.[/quote]
sto konkretno znaci ova recenica?
| veky (napisa): | | HijenA (napisa): | | kakav je to broj? |
Hm. Kakav je broj 6.723 ? (vjekovac, nisam tebe pitao! ; ) |
decimalan  
| Citat: |
Što misliš pod "kakav"? Na primjer, neprebrojiv je.
(*1) Ako kažeš da je cardX=alef1 , rekao si da je X neprebrojiv skup, i da su svi podskupovi od X ili ekvipotentni s X , ili prebrojivi (tu pod prebrojivim mislim na konačne). |
kad kazes ekvipotentni s X, onda mislis da imaju ista svojstva kao X (isti kardinalitet, prebrojivost/neprebrojivost i slicno)?
| Citat: |
(*2) Baš kao što bi s cardX=alef0 rekao da je X beskonačan, i da su svi podskupovi od X ili ekvipotentni s X , ili konačni.
Ok? |
ok...mislim da sam shvatio 
| Citat: |
| Citat: | | i sto znaci hipoteza kontinuuma? mozes pojasnit taj izraz? |
Hipoteza kontinuuma je da, kao što za primjer skupa kardinaliteta alef0 (najmanjeg beskonačnog skupa) imamo |N , tako bi primjer skupa kardinaliteta alef1 , najmanjeg _neprebrojivog_ skupa, bio |R . |
still don't get it. mislim da si me vise zbunio nego sto sam bio zbunjen 
zahvaljujem na linku...nismo li mi vecinu tih aksioma radili iz elementarne? samo ih nismo tako zvali 
| Citat: |
| Citat: | i sto uopce ZFC znaci?  |
Zermelo-Fraenkel theory with Choice. Teorija u kojoj se bar principijelo može raditi više od 99% dosadašnje matematike. |
again, zahvaljujem na objasnjenju 
| Citat: |
| Citat: | | znam da puno trazim, ali to me strasno interesira. |
Postoji Google. A uvijek možeš i mene uloviti na faksu.  |
ma znam da postoji google. inace bi se njemu prvi obratio. medjutim, kad sam trazio onaj skalarni produkt nad kompleksnim prostorima, nasao sam sve osim toga. besides, mislim da je ovo konkretno pitanje koje potpuno, i po svemu, spada na ovaj forum...mozda ne na UTB, ali u TS sigurno 
| Citat: |
| Citat: | | ne znam...mislio sam, isprva, da razgovaramo o brojevima no ispalo je da razgovaramo o skupovima. |
Hmm... pa brojevi su samo posebni skupovi.  Teorija skupova se dobrim dijelom bavi brojevima – kardinalnim i ordinalnim. Teorija brojeva, OTOH, se uglavnom bavi samo _konačnim_ brojevima – ovima manjima od alef0 . Teorija skupova se dobrim dijelom bavi brojevima – kardinalnim i ordinalnim. Teorija brojeva, OTOH, se uglavnom bavi samo _konačnim_ brojevima – ovima manjima od alef0 .  |
da...skuzio sam. zapravo...mene malo muce i definicije nekih, pa mogao bi reci, osnovnih pojmova. recimo...sto je to kardinalni broj?
po Mathworldu
| Mathworld (napisa): |
One of the first serious mathematical definitions of cardinal was the one devised by Gottlob Frege and Bertrand Russell, who defined a cardinal number as the set of all sets equipollent to A. |
sto konkretno znaci ova recenica?
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 0:28 čet, 10. 2. 2005 Naslov: Re: Alef0 i Alef1 Postano: 0:28 čet, 10. 2. 2005 Naslov: Re: Alef0 i Alef1 |
    |
|
|
[quote="HijenA"]
kad kazes ekvipotentni s X, onda mislis da imaju ista svojstva kao X (isti kardinalitet, prebrojivost/neprebrojivost i slicno)?
[/quote]
Za skupove A i B kazemo da su ekvipotentni ako postoji bijekcija f : A -> B.
[quote]
[quote]
[quote]i sto znaci [i]hipoteza kontinuuma[/i]? mozes pojasnit taj izraz?[/quote]
Hipoteza kontinuuma je da, kao što za primjer skupa kardinaliteta alef0 (najmanjeg beskonačnog skupa) imamo |N , tako bi primjer skupa kardinaliteta alef1 , najmanjeg _neprebrojivog_ skupa, bio |R .[/quote]
still don't get it. mislim da si me vise zbunio nego sto sam bio zbunjen :?
[/quote]
Postavlja se pitanje da li postoji beskonacan podskup od |R koji nije ekvipotentan niti sa |N, niti sa |R. Hipoteza kontinuuma kaze da takav skup ne postoji.
[quote]
zahvaljujem na linku...nismo li mi vecinu tih aksioma radili iz elementarne? samo ih nismo tako zvali :)
[/quote]
Ne.
[quote]
da...skuzio sam. zapravo...mene malo muce i definicije nekih, pa mogao bi reci, osnovnih pojmova. recimo...sto je to kardinalni broj?
po [url=http://mathworld.wolfram.com/CardinalNumber.html]Mathworldu[/url]
[quote="Mathworld"]
One of the first serious mathematical definitions of cardinal was the one devised by Gottlob Frege and Bertrand Russell, who defined a cardinal number as the set of all sets equipollent to A.[/quote]
sto konkretno znaci ova recenica?[/quote]
Ta recenica je pokusaj definicije kardinalnog broja, ali ne bas jako dobra, naime objekt o kojem se gore govori (skup svih skupova ekvipotentnih s A) u velikoj vecini slucajeva (osim za prazan skup) uopce nije skup.
Kardinalni brojevi se definiaju preko ordinalnih brojeva, ali mislim da nema smisla da to sada ovdje kucam (potrajalo bi), nego ti preporucam da uzmes neku knjigu iz knjiznice (mislim da postoji skripta iz TS-a od prof. Vukovica) i pogldas ono sto te interesira.
| HijenA (napisa): |
kad kazes ekvipotentni s X, onda mislis da imaju ista svojstva kao X (isti kardinalitet, prebrojivost/neprebrojivost i slicno)?
|
Za skupove A i B kazemo da su ekvipotentni ako postoji bijekcija f : A → B.
| Citat: |
| Citat: |
| Citat: | | i sto znaci hipoteza kontinuuma? mozes pojasnit taj izraz? |
Hipoteza kontinuuma je da, kao što za primjer skupa kardinaliteta alef0 (najmanjeg beskonačnog skupa) imamo |N , tako bi primjer skupa kardinaliteta alef1 , najmanjeg _neprebrojivog_ skupa, bio |R . |
still don't get it. mislim da si me vise zbunio nego sto sam bio zbunjen 
|
Postavlja se pitanje da li postoji beskonacan podskup od |R koji nije ekvipotentan niti sa |N, niti sa |R. Hipoteza kontinuuma kaze da takav skup ne postoji.
| Citat: |
zahvaljujem na linku...nismo li mi vecinu tih aksioma radili iz elementarne? samo ih nismo tako zvali 
|
Ne.
| Citat: |
da...skuzio sam. zapravo...mene malo muce i definicije nekih, pa mogao bi reci, osnovnih pojmova. recimo...sto je to kardinalni broj?
po Mathworldu
| Mathworld (napisa): |
One of the first serious mathematical definitions of cardinal was the one devised by Gottlob Frege and Bertrand Russell, who defined a cardinal number as the set of all sets equipollent to A. |
sto konkretno znaci ova recenica? |
Ta recenica je pokusaj definicije kardinalnog broja, ali ne bas jako dobra, naime objekt o kojem se gore govori (skup svih skupova ekvipotentnih s A) u velikoj vecini slucajeva (osim za prazan skup) uopce nije skup.
Kardinalni brojevi se definiaju preko ordinalnih brojeva, ali mislim da nema smisla da to sada ovdje kucam (potrajalo bi), nego ti preporucam da uzmes neku knjigu iz knjiznice (mislim da postoji skripta iz TS-a od prof. Vukovica) i pogldas ono sto te interesira.
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 1:24 čet, 10. 2. 2005 Naslov: Re: Alef0 i Alef1 Postano: 1:24 čet, 10. 2. 2005 Naslov: Re: Alef0 i Alef1 |
    |
|
|
[quote="HijenA"][quote="veky"]
Hm. Kakav je broj 6.723 ? (vjekovac, nisam tebe pitao! ; )[/quote]
decimalan :rotfl: ;-)[/quote]
Mhm. Okej, onda je alef1 kardinalan. :lol:
[quote]kad kazes ekvipotentni s X, onda mislis da imaju ista svojstva kao X (isti kardinalitet, prebrojivost/neprebrojivost i slicno)?[/quote]
Mislim da imaju isti kardinalitet. Time naravno i "prebrojivost/neprebrojivost". [size=9]Ovo "ista svojstva" se in a way svodi na to, ako uzmeš u obzir da su skupovi bez ikakve dodatne strukture takvi da je jedini zahtjev na izomorfizam, da bude bijekcija. Dakle, ako ne gledaš prirodu individualnih elemenata, sve što ti ostaje je njihov broj -- koliko ih ima.[/size]
[quote][quote]Hipoteza kontinuuma je da, kao što za primjer skupa kardinaliteta alef0 (najmanjeg beskonačnog skupa) imamo |N , tako bi primjer skupa kardinaliteta alef1 , najmanjeg _neprebrojivog_ skupa, bio |R .[/quote]
still don't get it. mislim da si me vise zbunio nego sto sam bio zbunjen :?[/quote]
Ok. Pogledaj izjavu [*2] gore. Kad to kažem na takav način, vidiš da je to definicija najmanjeg beskonačnog skupa, zar ne? That is, X je beskonačan, i svaki strogo manji (po kardinalitetu) od X je konačan.
E sad, da te netko pita primjer takvog skupa, mogao bi mu odgovoriti npr. " |N ". Ili " |Z ". Ili " |Q ". Zar ne?
E sad pogledaj izjavu [*1] . Ona je vrlo slična, samo zamijeni "beskonačan" sa sljedećom stepenicom, "neprebrojiv". So, to je definicija najmanjeg neprebrojivog skupa. That is, X je neprebrojiv, i svaki strogo manji (po kardinalitetu) od X je prebrojiv (uključivši i konačne).
Međutim, da te netko pita za primjer _takvog_ skupa... hm. Vjerojatno bi prvo pomislio " |R ". Na kraju krajeva, to i jest valjda prvi skup za koji se nauči da je neprebrojiv. No to još uvijek ne znači da je najmanji takav.
S druge strane, može se vidjeti da je |R ekvipotentan s \P(\N) . A \P(\N) ima strogo više elemenata od \N , i to *toliko više* da je tu tvrdnju čak za proizvoljan A ( card\P(A)>cardA ) prilično lako dokazati. :-)
Ukratko, |R je zaista ogroman skup. Da parafraziram standardni "argument" ljudi koji vjeruju u postojanje vanzemaljskih civilizacijâ, "bila bi šteta da tako ogromno prostranstvo bude nenastanjeno". Bila bi šteta da ta ogromna rupa između |R (odnosno \P(\N) ) i \N ne sadrži nijedan kardinalan broj. Pa ipak, naravno, to nije argument.
Vidjeli smo kvaziargumente za obje tvrdnje, zašto bi bilo "logično očekivati" da je card|R prvi nakon card\N , kao i zašto bi bilo "lijepo vjerovati" da između ima nešto. Sad bi možda bilo vrijeme da navedemo prave, math-ZFC argumente, i da vidimo kako stvari "zapravo" stoje... no to ne možemo. To je ova nezavisnost o kojoj mdoko pričaše gore. Jednostavno, ni jedna ni druga tvrdnja ne mogu se dokazati u ZFC .
[quote]zahvaljujem na linku...nismo li mi vecinu tih aksioma radili iz elementarne? samo ih nismo tako zvali :)[/quote]
Sumnjam. Možda sam u nekoj digresiji spomenuo neki :oops: ;-) , ali baš da smo ih _radili_, ne bih rekao.
[quote]ma znam da postoji google. inace bi se njemu prvi obratio. medjutim, kad sam trazio onaj skalarni produkt nad kompleksnim prostorima, nasao sam sve osim toga.[/quote]
Naravno. Trebala ti je konkretna formula, i nisi imao prave engleske riječi. No ovo je dijametralno suprotna stvar -- treba ti uvod u jedno dosta široko područje, i u njemu je terminologija prilično internacionalna -- a i ono što nije, ima smisla očekivati da će ti trebati prije ili kasnije, pa možeš naučiti. :-) Ako i u ovom postu bude hrpa stvari koje ne uspiješ pohvatati, vjerujem da ćeš i sam shvatiti da je jednostavnije uloviti mene na faksu IRL koji put. ;-)
[quote] besides, mislim da je ovo konkretno pitanje koje potpuno, i po svemu, spada na ovaj forum...mozda ne na UTB, ali u TS sigurno :)[/quote]
E vidiš, problem IMO leži u ovom "konkretno". :-) Na tvoje pitanje je odavno odgovoreno, ali to je otvorilo 5 drugih zanimljivih tema za raspravu. Nemam ništa protiv, no ovako imam osjećaj da se tvoja zbunjenost samo akumulira. Ako ti možeš handleati to, sve ok.
[quote]da...skuzio sam. zapravo...mene malo muce i definicije nekih, pa mogao bi reci, osnovnih pojmova. recimo...sto je to kardinalni broj?[/quote]
Najmanji ordinal u svojoj klasi ekvipotentnosti. :-)
Ordinali su generalizacija prirodnih brojeva -- posebno iskonstruirani skupovi kojima možeš brojiti. Na ordinalima možeš uvesti "relaciju" ekvipotentnosti ("relacija", kao i ostali pojmovi u toj grani poslije, su u navodnicima, jer to nije striktno relacija u smislu EM1 -- na primjer, nije relacija na nekom skupu, jer svi ordinali ne čine skup -- ali mnoge stvari slično vrijede), zna se kako: A je ekvipotentan s B :akko postoji bijekcija s A na B .
Sad se dokaže da je ta "relacija" zapravo "relacija ekvivalencije", pa svaki ordinal ima svoju "klasu". "Klase" su neprazne (baš kao u EM : ), a ordinali imaju (među ostalim) zanimljivo svojstvo da ako postoji ordinal s nekim svojstvom, onda uvijek postoji i najmanji takav. Dakle, u ovom slučaju, svaka "klasa ekvipotentnosti" ima najmanji element, i on se zove kardinalni broj.
[quote]One of the first serious mathematical definitions of cardinal was the one devised by Gottlob Frege and Bertrand Russell, who defined a cardinal number as the set of all sets equipollent to A.
sto konkretno znaci ova recenica?[/quote]
Puno lipih stvari, malo toga prihvatljivo današnjem mathu. :-o
Remember, taj Russel je isti onaj iz Russelovog paradoksa. ;-)
Pokušali su definirati, na primjer, broj 1 kao skup svih singletonova. Broj 2 kao skup svih parova. Broj alef0 kao skup svih beskonačnih prebrojivih skupova. (Broj 0 kao skup svih praznih skupova. ;-) ) Problem s tim pristupom, kao što mdoko reče, je to što to općenito nisu skupovi (osim ovog "skupa svih praznih skupova", koji je jednostavno {0} -- svi prazni skupovi su jednaki. : ) -- preveliki su za to.
Ukratko, greška je bila u tome što su ono opisano u mom gornjem odlomku napravili bez navodnika (i bez ordinala) -- stvaran skup svih skupova, relaciju ekvivalencije na njemu, klase koje su onda činile particiju... i naravno, definirati kardinalni broj na najprirodniji mogući način -- kao klasu ekvipotentnosti. As I said, to nije dobar pristup, jer te klase nisu skupovi, i tako bismo već u definiciji kardinalnih brojeva izašli iz svijeta ZFCa.
| HijenA (napisa): | | veky (napisa): |
Hm. Kakav je broj 6.723 ? (vjekovac, nisam tebe pitao! ; ) |
decimalan   |
Mhm. Okej, onda je alef1 kardinalan. 
| Citat: | | kad kazes ekvipotentni s X, onda mislis da imaju ista svojstva kao X (isti kardinalitet, prebrojivost/neprebrojivost i slicno)? |
Mislim da imaju isti kardinalitet. Time naravno i "prebrojivost/neprebrojivost". Ovo "ista svojstva" se in a way svodi na to, ako uzmeš u obzir da su skupovi bez ikakve dodatne strukture takvi da je jedini zahtjev na izomorfizam, da bude bijekcija. Dakle, ako ne gledaš prirodu individualnih elemenata, sve što ti ostaje je njihov broj – koliko ih ima.
| Citat: | | Citat: | | Hipoteza kontinuuma je da, kao što za primjer skupa kardinaliteta alef0 (najmanjeg beskonačnog skupa) imamo |N , tako bi primjer skupa kardinaliteta alef1 , najmanjeg _neprebrojivog_ skupa, bio |R . |
still don't get it. mislim da si me vise zbunio nego sto sam bio zbunjen  |
Ok. Pogledaj izjavu [*2] gore. Kad to kažem na takav način, vidiš da je to definicija najmanjeg beskonačnog skupa, zar ne? That is, X je beskonačan, i svaki strogo manji (po kardinalitetu) od X je konačan.
E sad, da te netko pita primjer takvog skupa, mogao bi mu odgovoriti npr. " |N ". Ili " |Z ". Ili " |Q ". Zar ne?
E sad pogledaj izjavu [*1] . Ona je vrlo slična, samo zamijeni "beskonačan" sa sljedećom stepenicom, "neprebrojiv". So, to je definicija najmanjeg neprebrojivog skupa. That is, X je neprebrojiv, i svaki strogo manji (po kardinalitetu) od X je prebrojiv (uključivši i konačne).
Međutim, da te netko pita za primjer _takvog_ skupa... hm. Vjerojatno bi prvo pomislio " |R ". Na kraju krajeva, to i jest valjda prvi skup za koji se nauči da je neprebrojiv. No to još uvijek ne znači da je najmanji takav.
S druge strane, može se vidjeti da je |R ekvipotentan s \P(\N) . A \P(\N) ima strogo više elemenata od \N , i to *toliko više* da je tu tvrdnju čak za proizvoljan A ( card\P(A)>cardA ) prilično lako dokazati. 
Ukratko, |R je zaista ogroman skup. Da parafraziram standardni "argument" ljudi koji vjeruju u postojanje vanzemaljskih civilizacijâ, "bila bi šteta da tako ogromno prostranstvo bude nenastanjeno". Bila bi šteta da ta ogromna rupa između |R (odnosno \P(\N) ) i \N ne sadrži nijedan kardinalan broj. Pa ipak, naravno, to nije argument.
Vidjeli smo kvaziargumente za obje tvrdnje, zašto bi bilo "logično očekivati" da je card|R prvi nakon card\N , kao i zašto bi bilo "lijepo vjerovati" da između ima nešto. Sad bi možda bilo vrijeme da navedemo prave, math-ZFC argumente, i da vidimo kako stvari "zapravo" stoje... no to ne možemo. To je ova nezavisnost o kojoj mdoko pričaše gore. Jednostavno, ni jedna ni druga tvrdnja ne mogu se dokazati u ZFC .
| Citat: | zahvaljujem na linku...nismo li mi vecinu tih aksioma radili iz elementarne? samo ih nismo tako zvali  |
Sumnjam. Možda sam u nekoj digresiji spomenuo neki   , ali baš da smo ih _radili_, ne bih rekao. , ali baš da smo ih _radili_, ne bih rekao.
| Citat: | | ma znam da postoji google. inace bi se njemu prvi obratio. medjutim, kad sam trazio onaj skalarni produkt nad kompleksnim prostorima, nasao sam sve osim toga. |
Naravno. Trebala ti je konkretna formula, i nisi imao prave engleske riječi. No ovo je dijametralno suprotna stvar – treba ti uvod u jedno dosta široko područje, i u njemu je terminologija prilično internacionalna – a i ono što nije, ima smisla očekivati da će ti trebati prije ili kasnije, pa možeš naučiti.  Ako i u ovom postu bude hrpa stvari koje ne uspiješ pohvatati, vjerujem da ćeš i sam shvatiti da je jednostavnije uloviti mene na faksu IRL koji put. Ako i u ovom postu bude hrpa stvari koje ne uspiješ pohvatati, vjerujem da ćeš i sam shvatiti da je jednostavnije uloviti mene na faksu IRL koji put. 
| Citat: | besides, mislim da je ovo konkretno pitanje koje potpuno, i po svemu, spada na ovaj forum...mozda ne na UTB, ali u TS sigurno  |
E vidiš, problem IMO leži u ovom "konkretno".  Na tvoje pitanje je odavno odgovoreno, ali to je otvorilo 5 drugih zanimljivih tema za raspravu. Nemam ništa protiv, no ovako imam osjećaj da se tvoja zbunjenost samo akumulira. Ako ti možeš handleati to, sve ok. Na tvoje pitanje je odavno odgovoreno, ali to je otvorilo 5 drugih zanimljivih tema za raspravu. Nemam ništa protiv, no ovako imam osjećaj da se tvoja zbunjenost samo akumulira. Ako ti možeš handleati to, sve ok.
| Citat: | | da...skuzio sam. zapravo...mene malo muce i definicije nekih, pa mogao bi reci, osnovnih pojmova. recimo...sto je to kardinalni broj? |
Najmanji ordinal u svojoj klasi ekvipotentnosti. 
Ordinali su generalizacija prirodnih brojeva – posebno iskonstruirani skupovi kojima možeš brojiti. Na ordinalima možeš uvesti "relaciju" ekvipotentnosti ("relacija", kao i ostali pojmovi u toj grani poslije, su u navodnicima, jer to nije striktno relacija u smislu EM1 – na primjer, nije relacija na nekom skupu, jer svi ordinali ne čine skup – ali mnoge stvari slično vrijede), zna se kako: A je ekvipotentan s B :akko postoji bijekcija s A na B .
Sad se dokaže da je ta "relacija" zapravo "relacija ekvivalencije", pa svaki ordinal ima svoju "klasu". "Klase" su neprazne (baš kao u EM : ), a ordinali imaju (među ostalim) zanimljivo svojstvo da ako postoji ordinal s nekim svojstvom, onda uvijek postoji i najmanji takav. Dakle, u ovom slučaju, svaka "klasa ekvipotentnosti" ima najmanji element, i on se zove kardinalni broj.
| Citat: | One of the first serious mathematical definitions of cardinal was the one devised by Gottlob Frege and Bertrand Russell, who defined a cardinal number as the set of all sets equipollent to A.
sto konkretno znaci ova recenica? |
Puno lipih stvari, malo toga prihvatljivo današnjem mathu. 
Remember, taj Russel je isti onaj iz Russelovog paradoksa. 
Pokušali su definirati, na primjer, broj 1 kao skup svih singletonova. Broj 2 kao skup svih parova. Broj alef0 kao skup svih beskonačnih prebrojivih skupova. (Broj 0 kao skup svih praznih skupova.  ) Problem s tim pristupom, kao što mdoko reče, je to što to općenito nisu skupovi (osim ovog "skupa svih praznih skupova", koji je jednostavno {0} – svi prazni skupovi su jednaki. : ) – preveliki su za to. ) Problem s tim pristupom, kao što mdoko reče, je to što to općenito nisu skupovi (osim ovog "skupa svih praznih skupova", koji je jednostavno {0} – svi prazni skupovi su jednaki. : ) – preveliki su za to.
Ukratko, greška je bila u tome što su ono opisano u mom gornjem odlomku napravili bez navodnika (i bez ordinala) – stvaran skup svih skupova, relaciju ekvivalencije na njemu, klase koje su onda činile particiju... i naravno, definirati kardinalni broj na najprirodniji mogući način – kao klasu ekvipotentnosti. As I said, to nije dobar pristup, jer te klase nisu skupovi, i tako bismo već u definiciji kardinalnih brojeva izašli iz svijeta ZFCa.
|
|
| [Vrh] |
|
fmb
Forumaš(ica)


Pridružen/a: 07. 02. 2004. (12:34:47)
Postovi: (B6)16
|
 Postano: 9:28 ned, 13. 2. 2005 Naslov: Re: Alef0 i Alef1 Postano: 9:28 ned, 13. 2. 2005 Naslov: Re: Alef0 i Alef1 |
    |
|
|
[quote="HijenA"]koja je razlika izmedju alef0 i alef1?
AFAIK alef0 je kardinalni broj skupa prirodnih brojeva.
moze mi netko u kratkim crtama objasnit razliku?[/quote]
Evo konacno da se javi i asistent iz teorije skupova... Sorry, tek sad sam vidila cijeli topic. Pa da ne citiram dijelove, jer su vecina tocni, evo kratkog sazetka o alefima... Osobito radi onih studenata koji to sad marljivo uce, ali mozda pomogne i onima koji su se izgubili u topicu. Sviju koji su se dobro snašli u prethodnim postovima upozoravam da ovo ne čitaju jer je veći dio ponavljanje.
Dakle, alefi su oznake za beskonacne kardinalne brojeve tj. brojeve elemenata beskonacnih skupova. Ideja je da imamo niz alef0<alef1<alef2<... u kojem nijedan beskonacni kard. broj nije izostavljen. Dva skupa imaju jednak kardinalni broj (ovo je definicija) ako postoji bijekcija između ta dva skupa. U priči o kardinalnim brojevima ne zanima nas nikakva dodatna struktura skupova kojima brojimo elemente tj. baš nas briga mogu li se njihovi elementi npr. množiti (kao npr. elementi iz N) ili komponirati (kao npr. skup svih funkcija R->R) ili urediti (kao npr. skupovi brojeva) itd. Nista od tog se ne smije podrazumijevati kad prebrajamo elemente nekog skupa kao sto se to nije pretpostavljalo ni kad smo prebrajali skup { :D , 8) , :twisted: } koji ima 3 elementa i ne znamo s njima ništa drugo (matematički :wink: ) raditi osim prebrojati ih.
Alef0 je dakle najmanji beskonačan k.broj i to je kardinalni broj bilo kojeg prebrojivog skupa (N, Z, Q, ... - svi oni imaju jednako mnogo elemenata i :!: samo takve koji imaju jednako elemenata kao N zovemo prebrojivi). Kardinalni broj skupa R (oznaka:[i]c[/i]) je strogo veci od alef0 tj. on je sigurno neki od onih ostalih alefa. On je mozda jednak alef1, a mozda i nije. Hipoteza kontinuuma kaze da jest. :!: Ali ona se ne moze ni dokazati ni opovrgnuti unutar standardne (ZFC) teorije skupova s kojom obično radimo kad pričamo o skupovima. Alef1 je pak prvi k. broj veći od alef0 (budući je dakle [i]c[/i] neki broj veći od alef0, a alef1 najmanji koji je od njeg veći, sigurno je alef1<=[i]c[/i]).
Što znamo o skupu s kardinalnim brojem alef1? Kao što veky reče, jedan (nažalost najjednostavniji) način da si predstavimo jedan takav skup je skup svih prebrojivih ordinala. Da sad ne odemo u priču o ordinalima, mogli bismo to reći i ovako: :idea: alef1 je skup svih dobrih uređaja na N tj. svih načina (dakle ne samo standardni <) da poredamo prirodne brojeve tako da su linearno uređeni, a da pritom svaki podskup od N u pojedinom takvom uređaju ima najmanji element. Primjer jednog uređaju < neekvivalentnog dobrog uređaja na N je idući: definiram da je n manji od m ako je m paran, a n neparan, ili su oba iste parnosti i n<m. To izgleda ovako:
0,2,4,6,8,...., svi parni, ..., 1,3,5,7,..., svi neparni,...
Evo, ne bih više. Nadam se da je bilo od pomoći. Pozdrav,
FMB :patkica: (puta alef1 :D )
| HijenA (napisa): | koja je razlika izmedju alef0 i alef1?
AFAIK alef0 je kardinalni broj skupa prirodnih brojeva.
moze mi netko u kratkim crtama objasnit razliku? |
Evo konacno da se javi i asistent iz teorije skupova... Sorry, tek sad sam vidila cijeli topic. Pa da ne citiram dijelove, jer su vecina tocni, evo kratkog sazetka o alefima... Osobito radi onih studenata koji to sad marljivo uce, ali mozda pomogne i onima koji su se izgubili u topicu. Sviju koji su se dobro snašli u prethodnim postovima upozoravam da ovo ne čitaju jer je veći dio ponavljanje.
Dakle, alefi su oznake za beskonacne kardinalne brojeve tj. brojeve elemenata beskonacnih skupova. Ideja je da imamo niz alef0<alef1<alef2<... u kojem nijedan beskonacni kard. broj nije izostavljen. Dva skupa imaju jednak kardinalni broj (ovo je definicija) ako postoji bijekcija između ta dva skupa. U priči o kardinalnim brojevima ne zanima nas nikakva dodatna struktura skupova kojima brojimo elemente tj. baš nas briga mogu li se njihovi elementi npr. množiti (kao npr. elementi iz N) ili komponirati (kao npr. skup svih funkcija R→R) ili urediti (kao npr. skupovi brojeva) itd. Nista od tog se ne smije podrazumijevati kad prebrajamo elemente nekog skupa kao sto se to nije pretpostavljalo ni kad smo prebrajali skup {  , ,  , ,  } koji ima 3 elementa i ne znamo s njima ništa drugo (matematički } koji ima 3 elementa i ne znamo s njima ništa drugo (matematički  ) raditi osim prebrojati ih. ) raditi osim prebrojati ih.
Alef0 je dakle najmanji beskonačan k.broj i to je kardinalni broj bilo kojeg prebrojivog skupa (N, Z, Q, ... - svi oni imaju jednako mnogo elemenata i  samo takve koji imaju jednako elemenata kao N zovemo prebrojivi). Kardinalni broj skupa R (oznaka:c) je strogo veci od alef0 tj. on je sigurno neki od onih ostalih alefa. On je mozda jednak alef1, a mozda i nije. Hipoteza kontinuuma kaze da jest. samo takve koji imaju jednako elemenata kao N zovemo prebrojivi). Kardinalni broj skupa R (oznaka:c) je strogo veci od alef0 tj. on je sigurno neki od onih ostalih alefa. On je mozda jednak alef1, a mozda i nije. Hipoteza kontinuuma kaze da jest.  Ali ona se ne moze ni dokazati ni opovrgnuti unutar standardne (ZFC) teorije skupova s kojom obično radimo kad pričamo o skupovima. Alef1 je pak prvi k. broj veći od alef0 (budući je dakle c neki broj veći od alef0, a alef1 najmanji koji je od njeg veći, sigurno je alef1⇐c). Ali ona se ne moze ni dokazati ni opovrgnuti unutar standardne (ZFC) teorije skupova s kojom obično radimo kad pričamo o skupovima. Alef1 je pak prvi k. broj veći od alef0 (budući je dakle c neki broj veći od alef0, a alef1 najmanji koji je od njeg veći, sigurno je alef1⇐c).
Što znamo o skupu s kardinalnim brojem alef1? Kao što veky reče, jedan (nažalost najjednostavniji) način da si predstavimo jedan takav skup je skup svih prebrojivih ordinala. Da sad ne odemo u priču o ordinalima, mogli bismo to reći i ovako:  alef1 je skup svih dobrih uređaja na N tj. svih načina (dakle ne samo standardni <) da poredamo prirodne brojeve tako da su linearno uređeni, a da pritom svaki podskup od N u pojedinom takvom uređaju ima najmanji element. Primjer jednog uređaju < neekvivalentnog dobrog uređaja na N je idući: definiram da je n manji od m ako je m paran, a n neparan, ili su oba iste parnosti i n<m. To izgleda ovako: alef1 je skup svih dobrih uređaja na N tj. svih načina (dakle ne samo standardni <) da poredamo prirodne brojeve tako da su linearno uređeni, a da pritom svaki podskup od N u pojedinom takvom uređaju ima najmanji element. Primjer jednog uređaju < neekvivalentnog dobrog uređaja na N je idući: definiram da je n manji od m ako je m paran, a n neparan, ili su oba iste parnosti i n<m. To izgleda ovako:
0,2,4,6,8,...., svi parni, ..., 1,3,5,7,..., svi neparni,...
Evo, ne bih više. Nadam se da je bilo od pomoći. Pozdrav,
FMB  (puta alef1 (puta alef1  ) )
_________________
"Have patience. Go where you must, and hope."
(Gandalf in J.R.R.Tolkien's "The Lord of the Rings")
|
|
| [Vrh] |
|
|














