| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
buba
Forumaš(ica)


Pridružen/a: 29. 10. 2004. (21:53:15)
Postovi: (57B)16
Spol: 
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
 Postano: 21:17 pon, 21. 2. 2005 Naslov: Postano: 21:17 pon, 21. 2. 2005 Naslov: |
    |
|
|
OvaK;
funkcija h je injekcija ako za svaki x, y iz domene vrijedi
x != y => h(x)!=h(y); e sad, ti imaš dvije injekcije (koristim tvoje oznake za funkcije f & g) f koja ide sa domene od f u |R; i g koja ide sa domene od g u |R; isto tako kompozicija je definirana ako f ide sa domene od f u svoju sliku; a g sa domene od g u svoju sliku, pri čemu slika od f mora biti podskup od domene od g; e, sad možemo dokazati ovu lemu :D daklem...
x =! y => f(x) =! f(y) //jer je f injekcija;
=> g(h(x)) =! g(h(y)) // ovo jer je g injekcija; kužiš? (njen argument je element iz slike od f)
E sad, pogledaš početeak i kraj.. i kaj smo dobili;
x =!y => g(h(x)) =! g(h(y)) :); tj. različitim elementima iz domene je kompozicija funkcija (f 0 g) pridružila različite elemente kodomene.
Funkcija je surjekcija ako za svaki y iz kodomene egzistira x iz domene takav da je f(x) = y (ovo je sama definicija); e, sad mi imamo dvije funkcije koje su surjekcije; znači za svaki y iz kodomene od f postoji x iz domene od f takav da je f(x) = y; ali isto tako i za svaki z iz kodomene od g egzistira y iz domene od g takav da je g (y)=z; no, uoči da je dotični y iz domene od g upravo onaj f(x) iz slike od f; znači imamo:
1) za svaki y iz kodomene od f [i]egzistira x[/i] iz domene od f takav da je
f(x)=y;
2) [i]za svaki z[/i] iz kodomene od g egzistira f(x) iz domene od g takav da je
[i] g(f(x))=z;[/i]
I pogledaš ono u "italics" i dobiš da za svaki z iz kodomene (f0g) egzistira x iz domene (f0g) takav da je g(f(x))=z :wink:
OvaK;
funkcija h je injekcija ako za svaki x, y iz domene vrijedi
x != y => h(x)!=h(y); e sad, ti imaš dvije injekcije (koristim tvoje oznake za funkcije f & g) f koja ide sa domene od f u |R; i g koja ide sa domene od g u |R; isto tako kompozicija je definirana ako f ide sa domene od f u svoju sliku; a g sa domene od g u svoju sliku, pri čemu slika od f mora biti podskup od domene od g; e, sad možemo dokazati ovu lemu  daklem... daklem...
x =! y => f(x) =! f(y) //jer je f injekcija;
=> g(h(x)) =! g(h(y)) // ovo jer je g injekcija; kužiš? (njen argument je element iz slike od f)
E sad, pogledaš početeak i kraj.. i kaj smo dobili;
x =!y => g(h(x)) =! g(h(y))  ; tj. različitim elementima iz domene je kompozicija funkcija (f 0 g) pridružila različite elemente kodomene. ; tj. različitim elementima iz domene je kompozicija funkcija (f 0 g) pridružila različite elemente kodomene.
Funkcija je surjekcija ako za svaki y iz kodomene egzistira x iz domene takav da je f(x) = y (ovo je sama definicija); e, sad mi imamo dvije funkcije koje su surjekcije; znači za svaki y iz kodomene od f postoji x iz domene od f takav da je f(x) = y; ali isto tako i za svaki z iz kodomene od g egzistira y iz domene od g takav da je g (y)=z; no, uoči da je dotični y iz domene od g upravo onaj f(x) iz slike od f; znači imamo:
1) za svaki y iz kodomene od f egzistira x iz domene od f takav da je
f(x)=y;
2) za svaki z iz kodomene od g egzistira f(x) iz domene od g takav da je
g(f(x))=z;
I pogledaš ono u "italics" i dobiš da za svaki z iz kodomene (f0g) egzistira x iz domene (f0g) takav da je g(f(x))=z 
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
 Postano: 1:03 uto, 22. 2. 2005 Naslov: Postano: 1:03 uto, 22. 2. 2005 Naslov: |
    |
|
|
Evo kratki i pregledniji dokaz...
Dakle, imamo funkcije
[latex]f:X\rightarrow Y\\ g:Y\rightarrow Z[/latex]
Ako su f,g surjekcije, tada je
[latex]f(X)=Y\\ g(Y)=Z[/latex]
Pa onda vrijedi:
[latex](g\circ f)(X)=g(f(X))=g(Y)=Z[/latex],
pa je g komponirano f surjekcija.
Ak' su f,g injekcije, onda vrijede inkluzije
[latex]f(x_{1})=f(x_{2})\Longrightarrow x_{1}=x_{2}\\ g(y_{1})=g(y_{2})\Longrightarrow y_{1}=y_{2}[/latex]
A to povlači ove inkluzije
[latex](g\circ f)(x_{1})=(g\circ f)(x_{2})\Longrightarrow g(f(x_{1}))=g(f(x_{2}))\Longrightarrow f(x_{1})=f(x_{2})\Longrightarrow x_{1}=x_{2}[/latex]
Stoga je g komponirano f injekcija.
Evo kratki i pregledniji dokaz...
Dakle, imamo funkcije
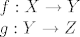
Ako su f,g surjekcije, tada je
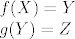
Pa onda vrijedi:
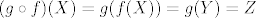 , ,
pa je g komponirano f surjekcija.
Ak' su f,g injekcije, onda vrijede inkluzije
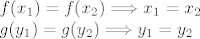
A to povlači ove inkluzije
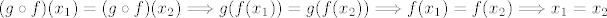
Stoga je g komponirano f injekcija.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
|
| [Vrh] |
|
defar
Forumaš(ica)


Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
 Postano: 15:11 uto, 22. 2. 2005 Naslov: Postano: 15:11 uto, 22. 2. 2005 Naslov: |
    |
|
|
[quote="Meri"][quote]
g komponirano f[/quote]
Mislim da ide [u]f komponirano sa g[/u]; ako je f unutarnja funkcija, onda ona djeluja prva; ke ne? :slonic:[/quote]
da, f djelluje prva, ali se u duhu pisanja s lijeva na desno, valjda, govori "g komponirano f". :-)
| Meri (napisa): |
Mislim da ide f komponirano sa g; ako je f unutarnja funkcija, onda ona djeluja prva; ke ne?  |
da, f djelluje prva, ali se u duhu pisanja s lijeva na desno, valjda, govori "g komponirano f". 
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
mea
Forumaš(ica)

Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 17:58 uto, 22. 2. 2005 Naslov: Postano: 17:58 uto, 22. 2. 2005 Naslov: |
    |
|
|
[quote="Meri"]
Valjda? Ja sam uvjerena da je f komponirano g; još smo bili i upozoreni na predavanju... 8)[/quote]
I ja tako mislim. Kaže se [i]f kompozicija g[/i] odnosno [i]f komponirano g[/i], čita se prvo ona koja prva djeluje.
[quote]da, f djelluje prva, ali se u duhu pisanja s lijeva na desno, valjda, govori "g komponirano f".[/quote]
Ispravnija duhovnost :) pisanja bila bi zdesna na lijevo...who cares... :wink:
| Meri (napisa): |
Valjda? Ja sam uvjerena da je f komponirano g; još smo bili i upozoreni na predavanju...  |
I ja tako mislim. Kaže se f kompozicija g odnosno f komponirano g, čita se prvo ona koja prva djeluje.
| Citat: | | da, f djelluje prva, ali se u duhu pisanja s lijeva na desno, valjda, govori "g komponirano f". |
Ispravnija duhovnost  pisanja bila bi zdesna na lijevo...who cares... pisanja bila bi zdesna na lijevo...who cares... 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
|










