| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
 Postano: 3:44 pet, 15. 4. 2005 Naslov: Postano: 3:44 pet, 15. 4. 2005 Naslov: |
    |
|
|
[quote="vjekovac"]Lako je pokazati da ne postoji linearna rekurzija s konstantnim koeficijentima. (Naime tada bi f morala biti specijalnog oblika.)[/quote]
Ja sam baš dobil' suprotno:
[latex]\displaystyle f(x)=\frac{e^{x}}{1+x+\frac{1}{2}x^{2}+\frac{x^{3}}{6}}\\
=f(x)+xf(x)+\frac{1}{2}x^{2}f(x)+\frac{x^{3}}{6}f(x)=e^{x}\\
\sum_{n\geq 0}a_{n}x^{n}
+x\sum_{n\geq 1}a_{n-1}x^{n-1}
+\frac{1}{2}x^{2}\sum_{n\geq 2}a_{n-2}x^{n-2}
+\frac{x^{3}}{6}\sum_{n\geq 3}a_{n-3}x^{n-3}=e^{x}\\
\sum_{n\geq 0}a_{n}x^{n}+\sum_{n\geq 1}a_{n-1}x^{n}+\sum_{n\geq 2}\frac{1}{2}a_{n-2}x^{n}+\sum_{n\geq 3}\frac{1}{6}a_{n-3}x^{n}=e^{x}\\
a_{0}+a_{1}x+a_{2}x^{2}+\sum_{n\geq 3}a_{n}x^{n}+
a_{0}x+a_{1}x^{2}+\sum_{n\geq 3}a_{n-1}x^{n}+
\frac{1}{2}a_{0}x^{2}+\sum_{n\geq 3}\frac{1}{2}a_{n-2}x^{n}+\sum_{n\geq 3}\frac{a_{n-3}}{6}x^{n}=e^{x}\\
a_{0}+(a_{0}+a_{1})x+(\frac{1}{2}a_{0}+a_{1}+a_{2})x^{2}+
\sum_{n\geq 3}(a_{n}+a_{n-1}+\frac{1}{2}a_{n-2}+\frac{a_{n-3}}{6})x^{n}=e^{x}[/latex]
Kako je [latex]e^{x}=\sum_{n\geq 0}\frac{x^{n}}{n!}[/latex], izjednačavanjem koeficijenata uz x na nultu, prvu i drugu, dobivamo sistem jednadžbi,
[latex]a_{0}=1\\
a_{0}+a_{1}=1\\
\frac{1}{2}a_{0}+a_{1}+a_{2}=\frac{1}{2}[/latex]
a rješenja sistema [latex]a_{0}=1, a_{1}=0, a_{2}=0[/latex] su očito početni uvjeti rekurzije, koja se dobije izjednačavanjem koeficijenata uz x na n-tu. Dakle, tražena rekurzija je
[latex]\displaystyle a_{n}+a_{n-1}+\frac{1}{2}a_{n-2}+\frac{1}{6}a_{n-3}=\frac{1}{n!}[/latex]
za n>=3.
| vjekovac (napisa): | | Lako je pokazati da ne postoji linearna rekurzija s konstantnim koeficijentima. (Naime tada bi f morala biti specijalnog oblika.) |
Ja sam baš dobil' suprotno:
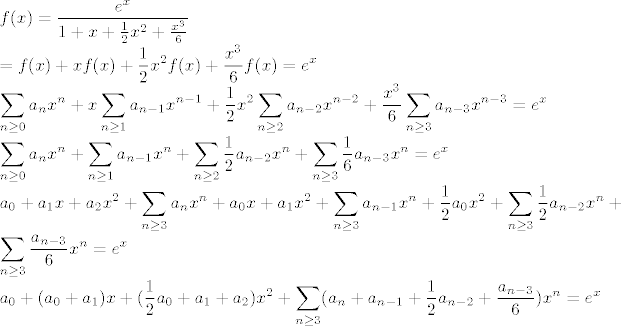
Kako je 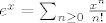 , izjednačavanjem koeficijenata uz x na nultu, prvu i drugu, dobivamo sistem jednadžbi, , izjednačavanjem koeficijenata uz x na nultu, prvu i drugu, dobivamo sistem jednadžbi,
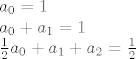
a rješenja sistema 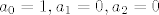 su očito početni uvjeti rekurzije, koja se dobije izjednačavanjem koeficijenata uz x na n-tu. Dakle, tražena rekurzija je su očito početni uvjeti rekurzije, koja se dobije izjednačavanjem koeficijenata uz x na n-tu. Dakle, tražena rekurzija je
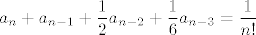
za n>=3.
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|








