| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 18:35 čet, 21. 4. 2005 Naslov: Postano: 18:35 čet, 21. 4. 2005 Naslov: |
    |
|
|
U petom se 1000x1000 kvadrat raspili na 10x20 pravokutnike. Ima ih 5000, sto je vise od broja krugova. Jedini problem je sto jedan krug moze zasijeci do 4 pravokutnika... rjesava se tako da se pravokutnici razmaknu malo vise od promjera kruga. Zbog toga ce ih biti manje od 5000, ali jos uvijek vise nego krugova (tocan broj je 4320, sto znaci da je krugova zapravo moglo biti 4319).
Meni su najzanimljivija rjesenja 3. zadatka. Trebalo je dokazati ovo:
[latex]\displaystyle{\sum_{i=0}^{\lfloor n/2\rfloor} {n-i\choose i} = F_{n+1}}[/latex]
(desno je (n+1)-vi Fibonaccijev broj)
"Sluzbeno" rjesenje je pokazati da sume zadovoljavaju Fibonaccijevu rekurziju s pomaknutim pocetnim uvjetima. Koristi se Pascalova formula za binomne koeficijente.
Moglo se dokazati kombinatorno: F_(n+1) je broj binarnih nizova duljine n-1 bez susjednih jedinica. Ako nizove grupiramo prema broju jedinica, dobivamu upravo sumu na lijevoj strani. Toga se sjetio Predrag Sladecek :miniklap:
Vrlo originalan dokaz ponudio je Crni :ok: Ubacio je sume bin. koeficijenata u funkciju izvodnicu i zamijenio redoslijed sumacije...
[latex]\displaystyle{\sum_{n\ge 0}\sum_{i=0}^{\lfloor n/2\rfloor} {n-i\choose i}x^n = \sum_{i\ge 0}\sum_{n\ge 2i }{n-i\choose i}x^n=[j=n-2i]=}[/latex]
[latex]\displaystyle{\sum_{i\ge 0}\sum_{j\ge 0} {2i+j-i\choose i}x^{2i+j}=\sum_{i\ge 0}x^{2i}\sum_{j\ge 0} {i+j\choose i}x^j=\sum_{i\ge 0}{x^{2i}\over (1-x)^{i+1}}=}[/latex]
[latex]\displaystyle{{1\over 1-x}\sum_{i\ge 0} \left({x^2\over 1-x}\right)^i={1\over 1-x}\cdot {1\over 1-{x^2\over 1-x}}={1\over 1-x-x^2}}[/latex]
Ovo je upravo funkcija izvodnica pomaknutih Fibonaccijevih brojeva. Gotovo!
U petom se 1000x1000 kvadrat raspili na 10x20 pravokutnike. Ima ih 5000, sto je vise od broja krugova. Jedini problem je sto jedan krug moze zasijeci do 4 pravokutnika... rjesava se tako da se pravokutnici razmaknu malo vise od promjera kruga. Zbog toga ce ih biti manje od 5000, ali jos uvijek vise nego krugova (tocan broj je 4320, sto znaci da je krugova zapravo moglo biti 4319).
Meni su najzanimljivija rjesenja 3. zadatka. Trebalo je dokazati ovo:
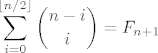
(desno je (n+1)-vi Fibonaccijev broj)
"Sluzbeno" rjesenje je pokazati da sume zadovoljavaju Fibonaccijevu rekurziju s pomaknutim pocetnim uvjetima. Koristi se Pascalova formula za binomne koeficijente.
Moglo se dokazati kombinatorno: F_(n+1) je broj binarnih nizova duljine n-1 bez susjednih jedinica. Ako nizove grupiramo prema broju jedinica, dobivamu upravo sumu na lijevoj strani. Toga se sjetio Predrag Sladecek 
Vrlo originalan dokaz ponudio je Crni  Ubacio je sume bin. koeficijenata u funkciju izvodnicu i zamijenio redoslijed sumacije... Ubacio je sume bin. koeficijenata u funkciju izvodnicu i zamijenio redoslijed sumacije...
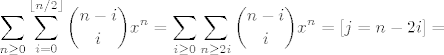
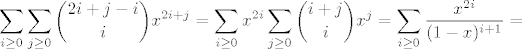
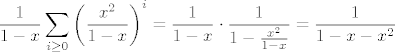
Ovo je upravo funkcija izvodnica pomaknutih Fibonaccijevih brojeva. Gotovo!
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
hermione
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gordan
Forumaš(ica)


Pridružen/a: 03. 11. 2002. (18:01:44)
Postovi: (192)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
|






