| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
 Postano: 9:18 pon, 21. 2. 2005 Naslov: Postano: 9:18 pon, 21. 2. 2005 Naslov: |
    |
|
|
Neka je S[k] skup svih skupova brojeva za koje vrijedi svojstvo, a brojevi su manji od k.
Pogledajmo skup S[k+2].
On moze ili ne mora sadrzavati element k+2.
1) ukoliko ga ne sadrzi, ima isto elemenata kao S[k+1].
2) ukoliko ga sadrzi, onda on moze nastaviti sve elemente skupa S[k], a moze biti i sam kao jedno rjesenje.
Rjesenje je kardinalitet tog skupa (mozemo ga oznaciti sa s[k]).
Dakle, rekurzija je s[k+2]=s[k]+s[k+1]+1.
Nju probaj rijesiti sam.
Neka je S[k] skup svih skupova brojeva za koje vrijedi svojstvo, a brojevi su manji od k.
Pogledajmo skup S[k+2].
On moze ili ne mora sadrzavati element k+2.
1) ukoliko ga ne sadrzi, ima isto elemenata kao S[k+1].
2) ukoliko ga sadrzi, onda on moze nastaviti sve elemente skupa S[k], a moze biti i sam kao jedno rjesenje.
Rjesenje je kardinalitet tog skupa (mozemo ga oznaciti sa s[k]).
Dakle, rekurzija je s[k+2]=s[k]+s[k+1]+1.
Nju probaj rijesiti sam.
_________________ 
Zadnja promjena: ahri; 3:08 uto, 22. 2. 2005; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
 Postano: 1:23 pon, 11. 4. 2005 Naslov: Postano: 1:23 pon, 11. 4. 2005 Naslov: |
    |
|
|
Mislim da je ahrijevo rješenje krivo.
Neka je [latex]S=\{s_{1},...,s_{n}\}[/latex] n-člani skup nekih uzastopnih prirodnih brojeva i neka je [latex]s_{1}<s_{2}<...<s_{n}[/latex]. Familija svih podskupova od S takvih da ne sadrže uzastopne elemente se može rastaviti u dvije disjunktne. Jedna ([latex]A_{1}[/latex]) sadrži samo one podskupove koji sadrže najmanji element, a druga ([latex]A_{2}[/latex]) sadrži samo one koji ne sadrže najmanji element. Uvedimo sada oznake:
[latex]a_{n}^{(1)}=|A_{1}|\\a_{n}^{(2)}=|A_{2}|\\a_{n}=a_{n}^{(1)}+a_{n}^{(2)}[/latex]
Neka je [latex]P\in A_{1}[/latex]. Tada je [latex]s_{1}\in P[/latex], pa svi ostali elementi iz P (ukoliko ih ima) čine neki podskup od [latex]\{s_{3},...,s_{n}\}[/latex] sa zadanim svojstvom. Tada je [latex]a_{n}^{(1)}=a_{n-2}[/latex]. Ako je [latex]P\in A_{2}[/latex], onda je [latex]s_{1}\notin P[/latex], pa P može biti bilo koji podskup sa zadanim svojstvom od [latex]\{ s_{2},...,s_{n}\}[/latex]. Prema tome je [latex]a_{n}^{(2)}=a_{n-1}[/latex]. Zbrajanjem ove dvije dobivene jednadžbe dobivamo rekurziju [latex]a_{n}=a_{n-1}+a_{n-2}[/latex] uz očite uvjete [latex]a_{0}=1, a_{1}=2[/latex]. Rješenje rekurzije je
[latex]\displaystyle a_{n}=\frac{3+\sqrt{5}}{2\sqrt{5}}\cdot \left( \frac{1+\sqrt{5}}{2}\right)^{n}-\frac{3-\sqrt{5}}{2\sqrt{5}}\cdot \left( \frac{1-\sqrt{5}}{2}\right)^{n}[/latex]
Pa bi onda rješenje zadatka bilo
[latex]\displaystyle\frac{3+\sqrt{5}}{2\sqrt{5}}\cdot \left( \frac{1+\sqrt{5}}{2}\right)^{n}-\frac{3-\sqrt{5}}{2\sqrt{5}}\cdot \left( \frac{1-\sqrt{5}}{2}\right)^{n}-1[/latex]
Mislim da je ahrijevo rješenje krivo.
Neka je 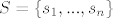 n-člani skup nekih uzastopnih prirodnih brojeva i neka je n-člani skup nekih uzastopnih prirodnih brojeva i neka je 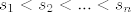 . Familija svih podskupova od S takvih da ne sadrže uzastopne elemente se može rastaviti u dvije disjunktne. Jedna ( . Familija svih podskupova od S takvih da ne sadrže uzastopne elemente se može rastaviti u dvije disjunktne. Jedna (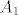 ) sadrži samo one podskupove koji sadrže najmanji element, a druga ( ) sadrži samo one podskupove koji sadrže najmanji element, a druga (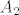 ) sadrži samo one koji ne sadrže najmanji element. Uvedimo sada oznake: ) sadrži samo one koji ne sadrže najmanji element. Uvedimo sada oznake:
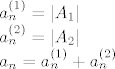
Neka je 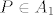 . Tada je . Tada je 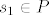 , pa svi ostali elementi iz P (ukoliko ih ima) čine neki podskup od , pa svi ostali elementi iz P (ukoliko ih ima) čine neki podskup od 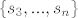 sa zadanim svojstvom. Tada je sa zadanim svojstvom. Tada je 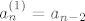 . Ako je . Ako je 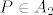 , onda je , onda je 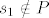 , pa P može biti bilo koji podskup sa zadanim svojstvom od , pa P može biti bilo koji podskup sa zadanim svojstvom od 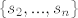 . Prema tome je . Prema tome je 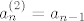 . Zbrajanjem ove dvije dobivene jednadžbe dobivamo rekurziju . Zbrajanjem ove dvije dobivene jednadžbe dobivamo rekurziju 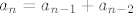 uz očite uvjete uz očite uvjete 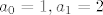 . Rješenje rekurzije je . Rješenje rekurzije je
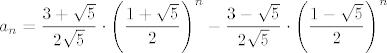
Pa bi onda rješenje zadatka bilo
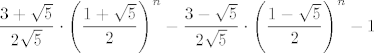
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:25 pon, 11. 4. 2005 Naslov: Postano: 12:25 pon, 11. 4. 2005 Naslov: |
    |
|
|
[quote="Tonci"][quote="Crni"]
Neka je [latex]P\in A_{1}[/latex]. Tada je [latex]s_{1}\in P[/latex], pa svi ostali elementi iz P ([b]ukoliko ih ima[/b]) čine neki podskup od [latex]\{s_{3},...,s_{n}\}[/latex] sa zadanim svojstvom. Tada je [latex]a_{n}^{(1)}=a_{n-2}[/latex]. [/quote]
A ukoliko ih nema? Onda cine prazan skup, a njega nismo racunali... Odatle Ahrijevih +1.[/quote]
Prazan skup je podskup [u]svakog[/u] skupa i ima svojstvo da ne sadrži dva uzastopna prirodna broja. To je bar trivijalno.
[color=red]Edit: Da malo bolje pojasnim Tonciju, skup [latex]P\setminus \{s_{1}\}[/latex] je podskup od [latex]\{s_{3},...,s_{n}\}[/latex] za zadanim svojstvom, pa makar bio i prazan. Dodatno definiramo: [latex]\{s_{k},...,s_{n}\}=\emptyset[/latex] za k>n.[/color]
| Tonci (napisa): | | Crni (napisa): |
Neka je 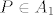 . Tada je . Tada je 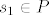 , pa svi ostali elementi iz P (ukoliko ih ima) čine neki podskup od , pa svi ostali elementi iz P (ukoliko ih ima) čine neki podskup od 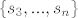 sa zadanim svojstvom. Tada je sa zadanim svojstvom. Tada je 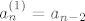 . . |
A ukoliko ih nema? Onda cine prazan skup, a njega nismo racunali... Odatle Ahrijevih +1. |
Prazan skup je podskup svakog skupa i ima svojstvo da ne sadrži dva uzastopna prirodna broja. To je bar trivijalno.
Edit: Da malo bolje pojasnim Tonciju, skup 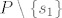 je podskup od je podskup od 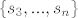 za zadanim svojstvom, pa makar bio i prazan. Dodatno definiramo: za zadanim svojstvom, pa makar bio i prazan. Dodatno definiramo: 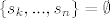 za k>n. za k>n.
Zadnja promjena: Crni; 14:37 uto, 12. 4. 2005; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 10:42 uto, 12. 4. 2005 Naslov: Postano: 10:42 uto, 12. 4. 2005 Naslov: |
    |
|
|
[quote="Crni"][quote="Anonymous"]pproblem je ekvivalentan ovome: odredi broj binarnih nizova bez uzastopnih jedinica[/quote]
Si siguran da tak' ide zadatak?
Stavljanjem jedinice ili nule na prvo mjesto niza duljine n>=1, jednoznačno se određuju brojevi na ostalih n-1 mjesta, pa je rješenje 2. Kaj je tu ekvivalentno?[/quote]
Ne kaze "[i]bez uzastopnih jedinica [b]i nula[/b][/i]", nego samo "[i]bez uzastopnih jedinica[/i]". 8)
U ekvivalentnost necu ulaziti. :o Treba ici na nastavu... :(
| Crni (napisa): | | Anonymous (napisa): | | pproblem je ekvivalentan ovome: odredi broj binarnih nizova bez uzastopnih jedinica |
Si siguran da tak' ide zadatak?
Stavljanjem jedinice ili nule na prvo mjesto niza duljine n>=1, jednoznačno se određuju brojevi na ostalih n-1 mjesta, pa je rješenje 2. Kaj je tu ekvivalentno? |
Ne kaze "bez uzastopnih jedinica i nula", nego samo "bez uzastopnih jedinica". 
U ekvivalentnost necu ulaziti.  Treba ici na nastavu... Treba ici na nastavu... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
 Postano: 20:00 uto, 12. 4. 2005 Naslov: Postano: 20:00 uto, 12. 4. 2005 Naslov: |
    |
|
|
[quote="Anonymous"]Crni, zadatak je opisan u knjizi prof. Veljana, str. 116, primjer 8.[/quote]
Ispričavam se zbog površnosti u čitanju. :oops:
[quote]Pise da postoji ocita bijekcija izmedju ta dva problema.[/quote]
Znači, tražimo broj nizova duljine n bez susjednih jedinica.
Neka je j broj jedinica u takvom nizu. Tada je broj nula očito n-j. Poslažimo sve jedinice jednu do druge. Zatim umetnemo između svake dvije jedinice po jednu nulu. Tada je broj umetnutih nula j-1, pa je broj preostalih nula n-2j+1. Sada imamo j+1 različitih blokova (j-1 između svake jedinice, jedan na kraju i jedan na početku niza) za umetanje ostalih nula, pa je broj načina za umetanje preostalih nula jednak broju slabih rastava broja n-2j+1 na j+1 dijelova i to je
[latex]\displaystyle {(n-2j+1)+(j+1)-1\choose (j+1)-1}={n-j+1\choose j}[/latex]
Kako broj jedinica nemre bit' veći od n, onda je broj svih nizova duljine n bez susjednih jedinica jednak
[latex]\displaystyle \sum_{j=0}^{n}{n-j+1\choose j}[/latex]
Sumu sam izračunal pomoću funkcije izvodnice:
[latex]\displaystyle f(x)=\sum_{n\geq 0}\sum_{k=0}^{n}{n-k+1\choose k}x^{n}\\
=\sum_{k\geq 0}\sum_{n\geq k}{n-k+1\choose k}x^{n}\\
=\sum_{k\geq 0}\sum_{n\geq 0}{n+1\choose k}x^{n+k}\\
=\sum_{n\geq 0}x^{n}\sum_{k\geq 0}{n+1\choose k}x^{k}\\
=\sum_{n\geq 0}x^{n}(1+x)^{n+1}\\
=(1+x)\sum_{n\geq 0}(x+x^{2})^{n}\\
=\frac{1+x}{1-x-x^{2}}[/latex]...
...pa se dalje faktorizacijom nazivnika, rastavom na parcijalne razlomke itd. dolazi do rezultata.
[color=red]Edit: ispričavam se zbog gluposti kaj sam ih bil' ovdje napisal' (tek sam kasnije skužil neke stvari). :oops: [/color]
| Anonymous (napisa): | | Crni, zadatak je opisan u knjizi prof. Veljana, str. 116, primjer 8. |
Ispričavam se zbog površnosti u čitanju. 
| Citat: | | Pise da postoji ocita bijekcija izmedju ta dva problema. |
Znači, tražimo broj nizova duljine n bez susjednih jedinica.
Neka je j broj jedinica u takvom nizu. Tada je broj nula očito n-j. Poslažimo sve jedinice jednu do druge. Zatim umetnemo između svake dvije jedinice po jednu nulu. Tada je broj umetnutih nula j-1, pa je broj preostalih nula n-2j+1. Sada imamo j+1 različitih blokova (j-1 između svake jedinice, jedan na kraju i jedan na početku niza) za umetanje ostalih nula, pa je broj načina za umetanje preostalih nula jednak broju slabih rastava broja n-2j+1 na j+1 dijelova i to je
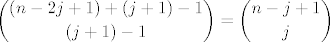
Kako broj jedinica nemre bit' veći od n, onda je broj svih nizova duljine n bez susjednih jedinica jednak
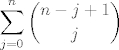
Sumu sam izračunal pomoću funkcije izvodnice:
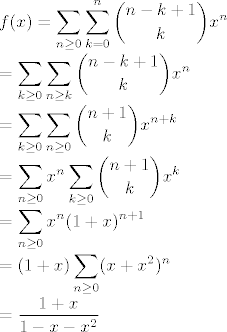 ... ...
...pa se dalje faktorizacijom nazivnika, rastavom na parcijalne razlomke itd. dolazi do rezultata.
Edit: ispričavam se zbog gluposti kaj sam ih bil' ovdje napisal' (tek sam kasnije skužil neke stvari). 
Zadnja promjena: Crni; 19:25 čet, 14. 4. 2005; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:50 sri, 13. 4. 2005 Naslov: Postano: 23:50 sri, 13. 4. 2005 Naslov: |
    |
|
|
Danas napokon pogledam na 116. str. Veljanove knjige i mislim si, koji mi je vrag bil' da ovo sve raspisujem. Uglavnom, bijekcija je fakat očita.
Dakle, za gosta koji nije skužil' očitost, funkcija koja od takvog niza radi skup prirodnih brojeva bez uzastopnih, šljaka na principu da skupi sve indekse pozicija na kojima stoje jedinice (kako nema uzastopnih jedinica, nema ni uzastopnih indeksa), pa onda od tih indeksa napravi skup koji očito da nema uzastopnih brojeva i koji je očito podskup od [n], jer i niz ima n pozicija. Isto tak se i od svakog takvog podskupa [latex]\{a_{1},...,a_{r}\}[/latex] od [n] generira niz bez uzastopnih jedinica:
[latex]---...---a_{1}-...-a_{r}----...---[/latex]
Dakle, na pozicije sa indeksima koji odgovaraju članovima skupa se stave jedinice, a na ostale pozicije nule.
Danas napokon pogledam na 116. str. Veljanove knjige i mislim si, koji mi je vrag bil' da ovo sve raspisujem. Uglavnom, bijekcija je fakat očita.
Dakle, za gosta koji nije skužil' očitost, funkcija koja od takvog niza radi skup prirodnih brojeva bez uzastopnih, šljaka na principu da skupi sve indekse pozicija na kojima stoje jedinice (kako nema uzastopnih jedinica, nema ni uzastopnih indeksa), pa onda od tih indeksa napravi skup koji očito da nema uzastopnih brojeva i koji je očito podskup od [n], jer i niz ima n pozicija. Isto tak se i od svakog takvog podskupa 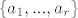 od [n] generira niz bez uzastopnih jedinica: od [n] generira niz bez uzastopnih jedinica:
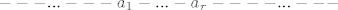
Dakle, na pozicije sa indeksima koji odgovaraju članovima skupa se stave jedinice, a na ostale pozicije nule.
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
|















