|
Obično (pot)puna indukcija znači sljedeće:
BAZA: Dokažemo tvrdnju za n=1.
KORAK: Uzmemo n>=2. Pretpostavimo da tvrdnja vrijedi za sve prirodne brojeve <n (tj. da vrijedi za 1,2,...,n-1) i iz toga izvedemo da tvrdnja vrijedi i za taj n.
To je samo jedna od varijanti indukcije.
Dakle, klasična indukcija bi bila (namjerno pišem n-1 umjesto n):
[latex]BAZA:\quad T(1)\\KORAK:\quad (\forall n\in\mathbf{N}\setminus\{1\})\Big(T(n-1)\Rightarrow T(n)\Big)[/latex]
dok je potpuna indukcija:
[latex]BAZA:\quad T(1)\\KORAK:\quad (\forall n\in\mathbf{N}\setminus\{1\})\Big(T(1)\&T(2)\&\ldots\&T(n-1)\Rightarrow T(n)\Big)[/latex]
(Neki bi logičar vjerojatno prigovorio da nam kod potpune indukcije niti ne treba BAZA, nego je možemo shvatiti kao tvrdnju iz KORAKA za n=1. Naime, dokazati T(1) je isto što i iz "ničega" izvesti T(1).)
Obično (pot)puna indukcija znači sljedeće:
BAZA: Dokažemo tvrdnju za n=1.
KORAK: Uzmemo n>=2. Pretpostavimo da tvrdnja vrijedi za sve prirodne brojeve <n (tj. da vrijedi za 1,2,...,n-1) i iz toga izvedemo da tvrdnja vrijedi i za taj n.
To je samo jedna od varijanti indukcije.
Dakle, klasična indukcija bi bila (namjerno pišem n-1 umjesto n):
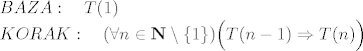
dok je potpuna indukcija:
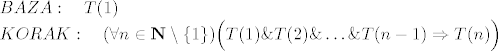
(Neki bi logičar vjerojatno prigovorio da nam kod potpune indukcije niti ne treba BAZA, nego je možemo shvatiti kao tvrdnju iz KORAKA za n=1. Naime, dokazati T(1) je isto što i iz "ničega" izvesti T(1).)
|




