| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 20:03 sri, 22. 6. 2005 Naslov: Što se traži u ovom zadatku? Postano: 20:03 sri, 22. 6. 2005 Naslov: Što se traži u ovom zadatku? |
    |
|
|
Neka je S n-člani skup. Koliko ima dvočlanih skupova {X, Y} gdje su X, Y podskupovi od S, a presjek X i Y je prazan skup.
-----
recimo da je n=10, a S=(1,2,3,.....,10). Ja sam mislio da je jedno od mogućih rješenja ((3,4),(6,7)). Dakle po meni prebrojim koliko ima dvočlanih podskupova od S (n povrh 2) pa to pomnožim sa (n povrh 2)-1 i sve skupa podjelim s 2 jer nije bitan poredak odabira skupova. Ali rješenje je (3^n - 1)/2 pa moje rješenje nije dobro. Pošto sam prilično siguran da je moje rješenje točno za moje čitanje zadatka može li mi netko molim vas reći što se onda zapravo traži u zadatku od mene :-(
Neka je S n-člani skup. Koliko ima dvočlanih skupova {X, Y} gdje su X, Y podskupovi od S, a presjek X i Y je prazan skup.
-----
recimo da je n=10, a S=(1,2,3,.....,10). Ja sam mislio da je jedno od mogućih rješenja ((3,4),(6,7)). Dakle po meni prebrojim koliko ima dvočlanih podskupova od S (n povrh 2) pa to pomnožim sa (n povrh 2)-1 i sve skupa podjelim s 2 jer nije bitan poredak odabira skupova. Ali rješenje je (3^n - 1)/2 pa moje rješenje nije dobro. Pošto sam prilično siguran da je moje rješenje točno za moje čitanje zadatka može li mi netko molim vas reći što se onda zapravo traži u zadatku od mene 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 20:28 sri, 22. 6. 2005 Naslov: Postano: 20:28 sri, 22. 6. 2005 Naslov: |
    |
|
|
Nigdje ne pise da su X i Y dvoclani! :)
:idea: [b]Ideja:[/b] Definiraj funkciju f:S->{0,1,2}:
f(x) = 1 <=> x € X
f(x) = 2 <=> x € Y
f(x) = 0 <=> inace (tj. x nije ni u jednom)
Dakle, pitanje je koliko ima takvih funkcija, uz dodatak da su funkcije f(x) i g(x) "jednake" ako za svaki x vrijedi f(x)=g(x)=0 ili f(x)+g(x)=3 (tj. smijemo zamijeniti jedinice i dvojke, odnosno smijemo zamijeniti mjesta skupovima X i Y jer je {X,Y} skup, a ne uredjeni par).
E sad: funkcija s gornjom definicijom ima 3^n. :) No, to ukljucuje i funkciju f(x)=0, sto bi za {X,Y} dalo jednoclani skup {0,0} (0="prazan skup"). Zato ih ima 3^n-1, a gornja opaska daje dijeljenje s 2 :arrow: ima ih (3^n-1)/2 :D
Jasno, to treba malo formalnije zapisati nego sto sam ja tu objasnio... ;)
Nigdje ne pise da su X i Y dvoclani! 
 Ideja: Definiraj funkciju f:S→{0,1,2}: Ideja: Definiraj funkciju f:S→{0,1,2}:
f(x) = 1 ⇔ x € X
f(x) = 2 ⇔ x € Y
f(x) = 0 ⇔ inace (tj. x nije ni u jednom)
Dakle, pitanje je koliko ima takvih funkcija, uz dodatak da su funkcije f(x) i g(x) "jednake" ako za svaki x vrijedi f(x)=g(x)=0 ili f(x)+g(x)=3 (tj. smijemo zamijeniti jedinice i dvojke, odnosno smijemo zamijeniti mjesta skupovima X i Y jer je {X,Y} skup, a ne uredjeni par).
E sad: funkcija s gornjom definicijom ima 3^n.  No, to ukljucuje i funkciju f(x)=0, sto bi za {X,Y} dalo jednoclani skup {0,0} (0="prazan skup"). Zato ih ima 3^n-1, a gornja opaska daje dijeljenje s 2 No, to ukljucuje i funkciju f(x)=0, sto bi za {X,Y} dalo jednoclani skup {0,0} (0="prazan skup"). Zato ih ima 3^n-1, a gornja opaska daje dijeljenje s 2  ima ih (3^n-1)/2 ima ih (3^n-1)/2 
Jasno, to treba malo formalnije zapisati nego sto sam ja tu objasnio... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Gost
|
 Postano: 10:30 čet, 23. 6. 2005 Naslov: Postano: 10:30 čet, 23. 6. 2005 Naslov: |
    |
|
|
Znam da gnjavim i da sam trebao ne sjedit na ušima na elementarnoj ali imam još par pitanja :-)
Prvi dio gornjeg zadatka pita koliko ima parova (x,y) disjunktnih podskupova od S? ((x,y podskupovi od S, x presjek y = prazan skup))
tu mi je jasno da trpam elemente iz S u tri kutije - X, Y i smeće. Jedan od slučajeva je da su x i y prazni, a cijeli S je u smeću. Tada dobivam (prazan skup, prazan skup) kao rješenje. Prazan skup je podskup od Sa, prazan skup presjek prazan skup je opet prazan skup pa je sve OK.
ALI u drugom dijelu zadatka više ne govorimo o paru (uređenom skupu X i Ya) već o njihovom skupu (neuređenom paru). Ja bi tada samo podjelio 3^n s 2 ali kao što ste rekli trebam izbacit taj specifičan slučaj {prazan skup, prazan skup}.
Dakle zaključak - kada govorimo o uređenoj k-torci (u našem slučaju 2-torka) onda je OK da bude (X=prazan skup, Y=prazan skup), ali kada se radi o skupu {X, Y} tada njegovi elementi ne smiju biti prazi skupovi, ali samo jedan element može
hvala!
Znam da gnjavim i da sam trebao ne sjedit na ušima na elementarnoj ali imam još par pitanja 
Prvi dio gornjeg zadatka pita koliko ima parova (x,y) disjunktnih podskupova od S? ((x,y podskupovi od S, x presjek y = prazan skup))
tu mi je jasno da trpam elemente iz S u tri kutije - X, Y i smeće. Jedan od slučajeva je da su x i y prazni, a cijeli S je u smeću. Tada dobivam (prazan skup, prazan skup) kao rješenje. Prazan skup je podskup od Sa, prazan skup presjek prazan skup je opet prazan skup pa je sve OK.
ALI u drugom dijelu zadatka više ne govorimo o paru (uređenom skupu X i Ya) već o njihovom skupu (neuređenom paru). Ja bi tada samo podjelio 3^n s 2 ali kao što ste rekli trebam izbacit taj specifičan slučaj {prazan skup, prazan skup}.
Dakle zaključak - kada govorimo o uređenoj k-torci (u našem slučaju 2-torka) onda je OK da bude (X=prazan skup, Y=prazan skup), ali kada se radi o skupu {X, Y} tada njegovi elementi ne smiju biti prazi skupovi, ali samo jedan element može
hvala!
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 13:54 čet, 23. 6. 2005 Naslov: Postano: 13:54 čet, 23. 6. 2005 Naslov: |
    |
|
|
Nisam siguran da sam razumio sto je tu pitanje... :-s
Ako te buni onaj -1... :| Kad imas situaciju X=Y=0 (prazan skup), tj. cijeli S je "u smecu" (kako si to lijepo i suptilno napisao ;)), onda je tvoj [b]dvoclani[/b] skup {X,Y} jednak {0,0}. :) No, skupovi ne trpe ponavljanje, pa je {0,0}={0}, dakle [b]jednoclan[/b], pa to ne mozemo brojati. 8) Zato taj slucaj ne racunamo, pa odatle -1. 8)
Nisam siguran da sam razumio sto je tu pitanje... 
Ako te buni onaj -1...  Kad imas situaciju X=Y=0 (prazan skup), tj. cijeli S je "u smecu" (kako si to lijepo i suptilno napisao Kad imas situaciju X=Y=0 (prazan skup), tj. cijeli S je "u smecu" (kako si to lijepo i suptilno napisao  ), onda je tvoj dvoclani skup {X,Y} jednak {0,0}. ), onda je tvoj dvoclani skup {X,Y} jednak {0,0}.  No, skupovi ne trpe ponavljanje, pa je {0,0}={0}, dakle jednoclan, pa to ne mozemo brojati. No, skupovi ne trpe ponavljanje, pa je {0,0}={0}, dakle jednoclan, pa to ne mozemo brojati.  Zato taj slucaj ne racunamo, pa odatle -1. Zato taj slucaj ne racunamo, pa odatle -1. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:42 pet, 24. 6. 2005 Naslov: Postano: 0:42 pet, 24. 6. 2005 Naslov: |
    |
|
|
Možda je bolje reći dvočlanih familija {X,Y} podskupova od S. Nađimo broj takvih familija.
Nađimo prvo broj familija koje sadrže prazan skup. To je očito [latex]2^{n}-1[/latex], jer ovaj drugi član familije može biti bilo koji neprazan skup.
Nađimo sada broj takvih familija koje sadrže samo neprazne podskupove. Neka je [latex]k\in \{ 1,...,n\}[/latex] i T k-člani podskup od S. Broj particija od T u dva bloka se računa pomoću rekurzije
S(k,2)=S(k-1,1)+2S(k-1,2)
ili jednostavnije zapisano
[latex]a_{k}=1+2a_{k-1}\\
a_{1}=0[/latex]
Rješenje rekurzije je [latex]a_{k}=2^{k-1}-1[/latex]. k-člani skup možemo izabrati na [latex]{n\choose k}[/latex] načina, pa je broj takvih familija jednak
[latex]\displaystyle\sum_{k=1}^{n}{n\choose k}(2^{k-1}-1)=\frac{1}{2}3^{n}-2^{n}+\frac{1}{2}[/latex]
Onda je rješenje zadatka
[latex]\displaystyle\frac{3^{n}-1}{2}[/latex]
za prirodni n.
Možda je bolje reći dvočlanih familija {X,Y} podskupova od S. Nađimo broj takvih familija.
Nađimo prvo broj familija koje sadrže prazan skup. To je očito 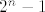 , jer ovaj drugi član familije može biti bilo koji neprazan skup. , jer ovaj drugi član familije može biti bilo koji neprazan skup.
Nađimo sada broj takvih familija koje sadrže samo neprazne podskupove. Neka je 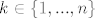 i T k-člani podskup od S. Broj particija od T u dva bloka se računa pomoću rekurzije i T k-člani podskup od S. Broj particija od T u dva bloka se računa pomoću rekurzije
S(k,2)=S(k-1,1)+2S(k-1,2)
ili jednostavnije zapisano
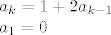
Rješenje rekurzije je 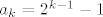 . k-člani skup možemo izabrati na . k-člani skup možemo izabrati na 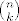 načina, pa je broj takvih familija jednak načina, pa je broj takvih familija jednak
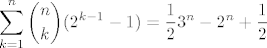
Onda je rješenje zadatka
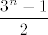
za prirodni n.
|
|
| [Vrh] |
|
Godot
Gost
|
 Postano: 1:00 pon, 24. 4. 2006 Naslov: Postano: 1:00 pon, 24. 4. 2006 Naslov: |
    |
|
|
[quote="gost"]
Prvi dio gornjeg zadatka pita koliko ima parova (x,y) disjunktnih podskupova od S?[/quote]
Moze li neko dati dati rjesenje na primjeu, kad je S={a,b}, odnosno S je dvoclani skup? Da li bi onda bilo rjesenje: (0,0), (0,a), (0,b), (a,0), (b,0), ((a,b),0), (0,(a,b)), (a,b), (b,a)?
Isto i za ovaj:
[quote="gost"]
Neka je S n-člani skup. Koliko ima dvočlanih skupova {X, Y} gdje su X, Y podskupovi od S, a presjek X i Y je prazan skup. [/quote]
Isto takav odgovor na primjeru kad je S={a,b} [ili S={a,b,c}(ako sa S={a,b} nije moguce)]. Po meni bi za S={a,b} trebalo biti: {0,a}, {0, b} {0, (a,b)} i {a,b}. Al mi tu nije jasno, ako je to uopce dobro, kako je {0,a} ili {0,b} dvoclani skup i zar nije {a,b}={0,(a,b)} ako uopce tako ide.
E sad moguce da su neke greske u ovim zagradama, pa neka ih neko tocno napise.
Hvala
| gost (napisa): |
Prvi dio gornjeg zadatka pita koliko ima parova (x,y) disjunktnih podskupova od S? |
Moze li neko dati dati rjesenje na primjeu, kad je S={a,b}, odnosno S je dvoclani skup? Da li bi onda bilo rjesenje: (0,0), (0,a), (0,b), (a,0), (b,0), ((a,b),0), (0,(a,b)), (a,b), (b,a)?
Isto i za ovaj:
| gost (napisa): |
Neka je S n-člani skup. Koliko ima dvočlanih skupova {X, Y} gdje su X, Y podskupovi od S, a presjek X i Y je prazan skup. |
Isto takav odgovor na primjeru kad je S={a,b} [ili S={a,b,c}(ako sa S={a,b} nije moguce)]. Po meni bi za S={a,b} trebalo biti: {0,a}, {0, b} {0, (a,b)} i {a,b}. Al mi tu nije jasno, ako je to uopce dobro, kako je {0,a} ili {0,b} dvoclani skup i zar nije {a,b}={0,(a,b)} ako uopce tako ide.
E sad moguce da su neke greske u ovim zagradama, pa neka ih neko tocno napise.
Hvala
|
|
| [Vrh] |
|
|







