|
Jako bih cijenio ako bi mi netko mogao pomoci oko dokaza teorema.
Tj, da je nxn matrica A slicna matrici J = (P^-1)AP koja ima s Jordanovih blokova na dijagonali, gdje je s broj linearno nezavisnih svojstvenih vektora od A.
Dokaz ide indukcijom po n.
Baza je ocita.
korak:
[i]I.[/i] neka je A singularna
[b]1.[/b] r = rang A < n
r je dimenzija stupcanog potprostora matrice kojega razapinje r linearno nezavisnih vektora [latex]w_i[/latex]
[latex]Aw_i = \lambda w_i[/latex] ili [latex]Aw_i = \lambda w_i + w_{i-1}[/latex] (po pretpostavci indukcije) [b]Kako to slijedi iz pretpostavke indukcije?![/b]
[b]2.[/b] nulprostor i stupcani prostor imaju presjek, dimenzije p. U 1. treba biti p niski koje polaze od tih svojstvenih vektora. Svaki od njih je u stupcanom potprostoru, pa je linearna kombinacija stupaca, dakle:
[latex]w_i = Ay_i[/latex]
[b]3.[/b]nulprostor je uvijek dimenzije n - r, stoga sadrzi n - p - r dodatnih vektora baze, [latex]z_i[/latex], koji leze izvan presjeka sa stupcanim prostorom.
Sad se pokaze da su ti vektori linearno nezavisni, kazemo da [latex]y_i[/latex] treba zapisati neposredno iza vektora [latex]w_i[/latex] iz kojeg je izveden i time nadopunjuje niske za [latex]\lambda _i = 0[/latex], a [latex]z_i[/latex] dolaze na sam kraj.
Ako je A regularna, oduzmemo joj neku svojstvenu vrijednost * I, pa postane singluarna.
Dakle, ako bi mi netko znao pojasniti ovaj, dokaz (pogotovo odgovoriti na boldano pitanje), puno bi mi pomogao :D[/b]
Jako bih cijenio ako bi mi netko mogao pomoci oko dokaza teorema.
Tj, da je nxn matrica A slicna matrici J = (P^-1)AP koja ima s Jordanovih blokova na dijagonali, gdje je s broj linearno nezavisnih svojstvenih vektora od A.
Dokaz ide indukcijom po n.
Baza je ocita.
korak:
I. neka je A singularna
1. r = rang A < n
r je dimenzija stupcanog potprostora matrice kojega razapinje r linearno nezavisnih vektora 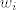
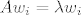 ili ili 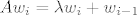 (po pretpostavci indukcije) Kako to slijedi iz pretpostavke indukcije?! (po pretpostavci indukcije) Kako to slijedi iz pretpostavke indukcije?!
2. nulprostor i stupcani prostor imaju presjek, dimenzije p. U 1. treba biti p niski koje polaze od tih svojstvenih vektora. Svaki od njih je u stupcanom potprostoru, pa je linearna kombinacija stupaca, dakle:
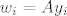
3.nulprostor je uvijek dimenzije n - r, stoga sadrzi n - p - r dodatnih vektora baze, 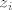 , koji leze izvan presjeka sa stupcanim prostorom. , koji leze izvan presjeka sa stupcanim prostorom.
Sad se pokaze da su ti vektori linearno nezavisni, kazemo da 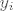 treba zapisati neposredno iza vektora treba zapisati neposredno iza vektora 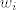 iz kojeg je izveden i time nadopunjuje niske za iz kojeg je izveden i time nadopunjuje niske za 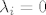 , a , a 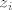 dolaze na sam kraj. dolaze na sam kraj.
Ako je A regularna, oduzmemo joj neku svojstvenu vrijednost * I, pa postane singluarna.
Dakle, ako bi mi netko znao pojasniti ovaj, dokaz (pogotovo odgovoriti na boldano pitanje), puno bi mi pomogao  [/b] [/b]
_________________
Bri
|






