| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Queen
Gost
|
 Postano: 15:59 pet, 1. 7. 2005 Naslov: Pomoc!!! Postano: 15:59 pet, 1. 7. 2005 Naslov: Pomoc!!! |
    |
|
|
Molio bi pomoc oko ovih zadataka, jer idem na komisiju.
1. f(x) = -arctg ( x^2 + 2x + 3 / 4 ) Odredite f ( [ -1,2> ) i f ^ -1 ( [ -pi / 4 , pi / 2 > )
2. f(x) = ln arcsin( x+2 / 5-x ) + sin ln( 2x -1 ) Odredite domenu
3. A = { arctg ( 3n^2 + 3 / 2n^2 + n ) : n iz N } odredite sup i inf skupa (ako postoje)
Sada, prvo gledam ovaj dio ( 3n^2 + 3 / 2n^2 + n ) i koristim Xn < Xn+1 => ( 3n^2 + 3 / 2n^2 + n ) < ( 3 (n+1)^2 + 3 / 2 (n+1)^2 + n+1 )
Kada se to izracuna dobijem -n^2 + 3n + 3 < 0 n1 = (3 - squr21)/2 n2 = (3 + squr21)/2 To je parabola okrenuta prema dolje i trazim gdje su n<0 i sada danje ne ide ...
5. NIz (an) je zadan rekurzivnom fordmulom
an+1 = 1/2 an^2 + 3/8 a1 = 3/8
Pokazi da je niz konvergentan i odredi mu limes
Sada , ja sam umjesto an stavio L da ko da sam dobio L = 1/2 L^2 + 3/8 i nakon racunala dobijem kvadretnu jednadbu -4L^2 + 8L - 3 =0 iz cega dobijem daj je L1 = 3/2 i L2 = 1/2
Da li treba provjetiti konvergentnos za oba ta L1 i L2 i kako odbaciti krivoga ...
Puno Hvala na svakoj pomoci !
Molio bi pomoc oko ovih zadataka, jer idem na komisiju.
1. f(x) = -arctg ( x^2 + 2x + 3 / 4 ) Odredite f ( [ -1,2> ) i f ^ -1 ( [ -pi / 4 , pi / 2 > )
2. f(x) = ln arcsin( x+2 / 5-x ) + sin ln( 2x -1 ) Odredite domenu
3. A = { arctg ( 3n^2 + 3 / 2n^2 + n ) : n iz N } odredite sup i inf skupa (ako postoje)
Sada, prvo gledam ovaj dio ( 3n^2 + 3 / 2n^2 + n ) i koristim Xn < Xn+1 => ( 3n^2 + 3 / 2n^2 + n ) < ( 3 (n+1)^2 + 3 / 2 (n+1)^2 + n+1 )
Kada se to izracuna dobijem -n^2 + 3n + 3 < 0 n1 = (3 - squr21)/2 n2 = (3 + squr21)/2 To je parabola okrenuta prema dolje i trazim gdje su n<0 i sada danje ne ide ...
5. NIz (an) je zadan rekurzivnom fordmulom
an+1 = 1/2 an^2 + 3/8 a1 = 3/8
Pokazi da je niz konvergentan i odredi mu limes
Sada , ja sam umjesto an stavio L da ko da sam dobio L = 1/2 L^2 + 3/8 i nakon racunala dobijem kvadretnu jednadbu -4L^2 + 8L - 3 =0 iz cega dobijem daj je L1 = 3/2 i L2 = 1/2
Da li treba provjetiti konvergentnos za oba ta L1 i L2 i kako odbaciti krivoga ...
Puno Hvala na svakoj pomoci !
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 19:05 pet, 1. 7. 2005 Naslov: Postano: 19:05 pet, 1. 7. 2005 Naslov: |
    |
|
|
Mozda mi se cini, ali nema zadatka s brojem 4. :grebgreb:
Ne da mi se sve, pa samo limes. 8) Stos s uvrstavanjem L mozes raditi tek ako pokazes da uopce imas limes! :-s
Primjer: a1 = 1, a(n+1) = -an (dakle: 1, -1, 1, -1,...)
L = -L => L = 0 => limes je 0 (a niz ocito ima gomilista -1 i 1, pa nema limes)
Za tvoj zadatak (indukcijom po n):
Tvrdnja: 0 < an < 1/2
1. 0 < a1 = 3/8 < 4/8 = 1/2
Pretp. da je 0 < ak < 1/2 za k<n
2. an = 1/2 a(n-1)^2 + 3/8 < 1/2 (1/2)^2 + 3/8 = 1/2 => an < 1/2
(an > 0 je ocito)
Dakle, imas omedjenu funkciju.
Dapace, a(n+1) > an. Pretpostavimo suprotno: postoji k a(k+1) <= ak
ak >= a(k+1) = 1/2 ak^2 + 3/8 / *8
8ak >= 4ak^2 + 3
4ak^2 - 8ak + 3 <= 0
4(ak - 1)^2 - 1 <= 0
4(ak - 1)^2 <= 1
2|ak - 1| <= 1 (ak < 1/2 => ak-1 < -1/2 < 0 => |ak-1| = 1-ak)
1 - ak <= 1/2
ak >= 1/2 (kontradikcija s ak < 1/2)
Dakle, niz je omedjen i monoton (dapace, monotono rastuci) :arrow: konvergentan. :D
Sad uvrstis L:
L = 1/2 L^2 + 3/8
L^2-2L+1=1/4
(L-1)^2=1/4
L-1=1/2 ili L-1=-1/2
L=3/2 ili L=1/2
Posto su svi an<1/2, limes ne moze biti 3/2 :arrow: limes je 1/2. 8)
P.S. Umalo nisam odgovorio na ovo; de malo informativniji subject ubuduce... :roll:
Mozda mi se cini, ali nema zadatka s brojem 4. 
Ne da mi se sve, pa samo limes.  Stos s uvrstavanjem L mozes raditi tek ako pokazes da uopce imas limes! Stos s uvrstavanjem L mozes raditi tek ako pokazes da uopce imas limes! 
Primjer: a1 = 1, a(n+1) = -an (dakle: 1, -1, 1, -1,...)
L = -L => L = 0 => limes je 0 (a niz ocito ima gomilista -1 i 1, pa nema limes)
Za tvoj zadatak (indukcijom po n):
Tvrdnja: 0 < an < 1/2
1. 0 < a1 = 3/8 < 4/8 = 1/2
Pretp. da je 0 < ak < 1/2 za k<n
2. an = 1/2 a(n-1)^2 + 3/8 < 1/2 (1/2)^2 + 3/8 = 1/2 => an < 1/2
(an > 0 je ocito)
Dakle, imas omedjenu funkciju.
Dapace, a(n+1) > an. Pretpostavimo suprotno: postoji k a(k+1) <= ak
ak >= a(k+1) = 1/2 ak^2 + 3/8 / *8
8ak >= 4ak^2 + 3
4ak^2 - 8ak + 3 <= 0
4(ak - 1)^2 - 1 <= 0
4(ak - 1)^2 <= 1
2|ak - 1| <= 1 (ak < 1/2 => ak-1 < -1/2 < 0 => |ak-1| = 1-ak)
1 - ak <= 1/2
ak >= 1/2 (kontradikcija s ak < 1/2)
Dakle, niz je omedjen i monoton (dapace, monotono rastuci)  konvergentan. konvergentan. 
Sad uvrstis L:
L = 1/2 L^2 + 3/8
L^2-2L+1=1/4
(L-1)^2=1/4
L-1=1/2 ili L-1=-1/2
L=3/2 ili L=1/2
Posto su svi an<1/2, limes ne moze biti 3/2  limes je 1/2. limes je 1/2. 
P.S. Umalo nisam odgovorio na ovo; de malo informativniji subject ubuduce... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Ana
Forumaš(ica)


Pridružen/a: 16. 01. 2005. (20:41:07)
Postovi: (89)16
Spol: 
|
 Postano: 22:46 pet, 1. 7. 2005 Naslov: Postano: 22:46 pet, 1. 7. 2005 Naslov: |
    |
|
|
Evo drugog (za ostale nisam sigurna):
1. (5 - x) različito od 0 (jer je to nazivnik)
2. ( x+2 / 5-x ) iz intervala od -1 do 1, tj. (-1) <= (x+2 / 5-x ) <= 1 (mora biti u domeni arcsin-a)
3. arcsin( x+2 / 5-x ) > 0 (jer je pod logaritmom)
4. ( 2x -1 ) > 0 (kao kod 2.)
5. ln( 2x -1 ) ok za sve (jer je domena sinusa cijeli R)
Naravno, izračunaš dane nejednadžbe i domena je presjek uvjeta od 1. - 5. (mislim da bi trebalo ispasti od 1/2, 3/2).
Naravno, nisam sigurna u ovo pa molim da me svi, koji vide da sam pogriješila, isprave...
Sretno na ispitu! :wink:
Evo drugog (za ostale nisam sigurna):
1. (5 - x) različito od 0 (jer je to nazivnik)
2. ( x+2 / 5-x ) iz intervala od -1 do 1, tj. (-1) <= (x+2 / 5-x ) <= 1 (mora biti u domeni arcsin-a)
3. arcsin( x+2 / 5-x ) > 0 (jer je pod logaritmom)
4. ( 2x -1 ) > 0 (kao kod 2.)
5. ln( 2x -1 ) ok za sve (jer je domena sinusa cijeli R)
Naravno, izračunaš dane nejednadžbe i domena je presjek uvjeta od 1. - 5. (mislim da bi trebalo ispasti od 1/2, 3/2).
Naravno, nisam sigurna u ovo pa molim da me svi, koji vide da sam pogriješila, isprave...
Sretno na ispitu! 
|
|
| [Vrh] |
|
Ana
Forumaš(ica)


Pridružen/a: 16. 01. 2005. (20:41:07)
Postovi: (89)16
Spol: 
|
|
| [Vrh] |
|
amimica
Forumaš(ica)

Pridružen/a: 14. 04. 2004. (15:40:42)
Postovi: (CA)16
|
 Postano: 18:47 ned, 3. 7. 2005 Naslov: Postano: 18:47 ned, 3. 7. 2005 Naslov: |
    |
|
|
1. Nacrtaj parabolu g(x)=-x^2/4-x/2-3/4 i tada se s grafa vidi da je g([-1,2>)=[-11/4,-1/2>. Ako definiramo h(x)=arctg(x), onda opet iz grafa funkcije h čitamo f([-1,2>)=h(g([-1,2>))=h([-11/4,-1/2>)=[-arctg(11/4),arctg(1/2)>.
Napomena: arctg je neparna funkcija, pa je arctg(-x)=-arctg x
Kada tražiš f^{-1}([-pi/4,pi/2>) zapravo rješavaš dvije nejednadžbe
[latex]
-\frac{\pi}{4}\leq-\mathrm{arctg}\left(\frac{x^2+2x+3}{4}\right)<\frac{\pi}{2}
[/latex]
(druga je uvijek ispunjena jer je slika funkcije arctg <-pi/2,pi/2>)
i dobije se rješenje
[latex]
[-1-\sqrt{2},-1+\sqrt{2}]
[/latex]
3. Dobije se kvadratna nejednadžba -n^2+3n+3<0 i sada je za
[latex]
n>\frac{3+\sqrt{21}}{2}\approx 3.791
[/latex]
x_n<x_{n+1},
tj. imamo ovakvu situaciju
x_1>=x_2>=x_3>=x_4<x_5<x_6<x_7<...,
pa je (arctg je rastuća)
inf S=arctg(x_4)=arctg(51/36)
sup S=max{arctg x_1,lim_n x_n}=max{arctg(2),arctg(3/2)}=arctg(2)
1. Nacrtaj parabolu g(x)=-x^2/4-x/2-3/4 i tada se s grafa vidi da je g([-1,2>)=[-11/4,-1/2>. Ako definiramo h(x)=arctg(x), onda opet iz grafa funkcije h čitamo f([-1,2>)=h(g([-1,2>))=h([-11/4,-1/2>)=[-arctg(11/4),arctg(1/2)>.
Napomena: arctg je neparna funkcija, pa je arctg(-x)=-arctg x
Kada tražiš f^{-1}([-pi/4,pi/2>) zapravo rješavaš dvije nejednadžbe
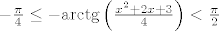
(druga je uvijek ispunjena jer je slika funkcije arctg ←pi/2,pi/2>)
i dobije se rješenje
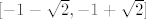
3. Dobije se kvadratna nejednadžba -n^2+3n+3<0 i sada je za
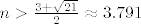
x_n<x_{n+1},
tj. imamo ovakvu situaciju
x_1>=x_2>=x_3>=x_4<x_5<x_6<x_7<...,
pa je (arctg je rastuća)
inf S=arctg(x_4)=arctg(51/36)
sup S=max{arctg x_1,lim_n x_n}=max{arctg(2),arctg(3/2)}=arctg(2)
|
|
| [Vrh] |
|
Queen
Gost
|
|
| [Vrh] |
|
Queen
Gost
|
|
| [Vrh] |
|
|







