|
[quote="Jadran"]1.U ovisnosti o parametru aeR odredite broj realnih rjesenja jednadzbe
(x^2+1)^(1/3) - (x)^(2/3)=a[/quote]
Tako je. Promatramo funkciju zadanu formulom
[latex]f(x)=(x^2+1)^{\frac{1}{3}}-(x^2)^{\frac{1}{3}}[/latex]
Nakon malo deriviranja i računanja limesa vidi se da:
f strogo raste na <-oo,0], a strogo pada na [0,+oo>
[latex]\lim_{x\to -\infty}f(x)=0,\quad\lim_{x\to +\infty}f(x)=0[/latex]
f(0)=1
Iz gornjeg slijedi (možeš si ugrubo skicirati graf da ti bude lakše):
za a€<-oo,0]u<1,+oo> jdžba f(x)=a nema rješenja
za a=1 jdžba f(x)=a ima jedno rješenje (i to je x=0)
za a€<0,1> jdžba f(x)=a ima dva rješenja
[quote="Jadran"]
2.Izracunajte
∑ n=0 do beskonačno ( (n + 1)(n + 2)(n + 3) / (2^n) )[/quote]
Najjednostavnije je ovako:
Jednakost
[latex]\sum_{n=0}^{\infty}x^n=\frac{1}{1-x},\quad |x|<1[/latex]
triput deriviramo pa dobijemo
[latex]\sum_{n=3}^{\infty}n(n-1)(n-2) x^{n-3}=\frac{6}{(1-x)^4},\quad |x|<1[/latex]
Sada malo pomaknemo indeks sumacije (pišemo n+3 umjesto n):
[latex]\sum_{n=0}^{\infty}(n+3)(n+2)(n+1) x^{n}=\frac{6}{(1-x)^4},\quad |x|<1[/latex]
i uvrstimo x=1/2
[latex]\sum_{n=0}^{\infty}(n+3)(n+2)(n+1) (\frac{1}{2})^{n}=\frac{6}{(1-\frac{1}{2})^4}=96[/latex]
| Jadran (napisa): | 1.U ovisnosti o parametru aeR odredite broj realnih rjesenja jednadzbe
(x^2+1)^(1/3) - (x)^(2/3)=a |
Tako je. Promatramo funkciju zadanu formulom
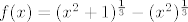
Nakon malo deriviranja i računanja limesa vidi se da:
f strogo raste na ←oo,0], a strogo pada na [0,+oo>
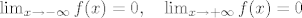
f(0)=1
Iz gornjeg slijedi (možeš si ugrubo skicirati graf da ti bude lakše):
za a€←oo,0]u<1,+oo> jdžba f(x)=a nema rješenja
za a=1 jdžba f(x)=a ima jedno rješenje (i to je x=0)
za a€<0,1> jdžba f(x)=a ima dva rješenja
| Jadran (napisa): |
2.Izracunajte
∑ n=0 do beskonačno ( (n + 1)(n + 2)(n + 3) / (2^n) ) |
Najjednostavnije je ovako:
Jednakost
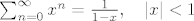
triput deriviramo pa dobijemo
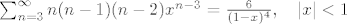
Sada malo pomaknemo indeks sumacije (pišemo n+3 umjesto n):
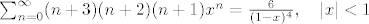
i uvrstimo x=1/2
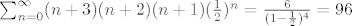
|





