| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 20:33 sri, 7. 9. 2005 Naslov: Nezavisne slučajne varijable Postano: 20:33 sri, 7. 9. 2005 Naslov: Nezavisne slučajne varijable |
    |
|
|
Molim jednu malu pomoć, ako bi mi netko mogao dokazat... X, Y, Z nezavisne slučajne varijable. Dokaži da su tad i X+Y i Z nezavisne! Ili X, Y, Z nezavisne, g proizvoljna fja. Da li su g(X,Y) i Z nezavisne??? Puno hvala!!
Molim jednu malu pomoć, ako bi mi netko mogao dokazat... X, Y, Z nezavisne slučajne varijable. Dokaži da su tad i X+Y i Z nezavisne! Ili X, Y, Z nezavisne, g proizvoljna fja. Da li su g(X,Y) i Z nezavisne??? Puno hvala!!
|
|
| [Vrh] |
|
alf
Forumaš(ica)


Pridružen/a: 29. 04. 2003. (20:53:54)
Postovi: (30)16
Spol: 
Lokacija: ZG
|
 Postano: 10:50 čet, 8. 9. 2005 Naslov: Postano: 10:50 čet, 8. 9. 2005 Naslov: |
    |
|
|
Sto mislis o ovome:
Slucaj [b]X+Y i Z:[/b]
[b]Pretpostavka:[/b] X,Y,Z su nezavisni tj. [latex] \forall A,B,C \subseteq R [/latex] vrijedi
[latex]
P(X \in A, Y \in B, Z \in C)=P(X \in A)P(Y \in B)P(Z \in C)[/latex]
[b]Tvrdnja:[/b]
X+Y i Z su nezavisni tj. [latex]
\forall A,B \subseteq R [/latex] vrijedi [latex]
P(X +Y \in A, Z \in B)=P(X+Y \in A)P(Z \in B)
[/latex]
dokaz:
Pretpostavimo suprotno, tj da [latex]
\exists A,B \subseteq R[/latex] t.d. vrijedi
[latex]
P(X+Y \in A,Z \in B) \neq P(X+Y \in A)P(Z \in B) (*)
[/latex]
Neka je
[latex]
C=\{ \omega_i \in \Omega : X(\omega_i)+Y(\omega_i) \in A \}
[/latex]
Sada
[latex] \forall \omega_i \in \Omega[/latex]
definiramo skup [latex] A_i=A - Y(\omega_i)[/latex]
Stavimo
[latex] C_y=\{ \omega \in \Omega : X(\omega) \in \bigcup_i A_i \}[/latex]
Analogno definiramo [latex]C_x[/latex] i vrijedi da je [latex]C=C_y=C_x[/latex]
Stoga mozemo pisati da je:
[latex] P(X+Y \in A)=P(X \in C_y, Y \in C_x)=[/latex](zbog nezavisnosti od X i Y)[latex]=P(X \in C_y)P(Y \in C_x)[/latex]
Sada (*) prelazi u:
[latex]
P(X\in C_y,Y \in C_x,Z \in B) \neq P(X \in C_y)P(Y \in C_x)P(Z \in B)
[/latex]
Sto je kontradikcija s nezavisnoscu od X,Y,Z
Q.E.D.
Sto mislis o ovome:
Slucaj X+Y i Z:
Pretpostavka: X,Y,Z su nezavisni tj. 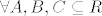 vrijedi vrijedi
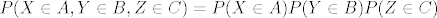
Tvrdnja:
X+Y i Z su nezavisni tj. 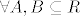 vrijedi vrijedi 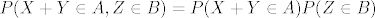
dokaz:
Pretpostavimo suprotno, tj da 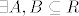 t.d. vrijedi t.d. vrijedi
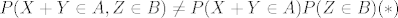
Neka je
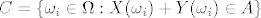
Sada
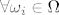
definiramo skup 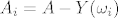
Stavimo
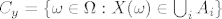
Analogno definiramo 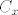 i vrijedi da je i vrijedi da je 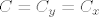
Stoga mozemo pisati da je:
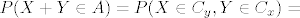 (zbog nezavisnosti od X i Y) (zbog nezavisnosti od X i Y)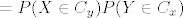
Sada (*) prelazi u:
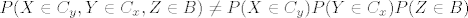
Sto je kontradikcija s nezavisnoscu od X,Y,Z
Q.E.D.
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 18:47 čet, 22. 9. 2005 Naslov: Re: Nezavisne slučajne varijable Postano: 18:47 čet, 22. 9. 2005 Naslov: Re: Nezavisne slučajne varijable |
    |
|
|
[quote="Anonymous"]X, Y, Z nezavisne, g proizvoljna fja. Da li su g(X,Y) i Z nezavisne??? Puno hvala!![/quote]
novija verzija knjige, zadatak 18, str. 165
| Anonymous (napisa): | | X, Y, Z nezavisne, g proizvoljna fja. Da li su g(X,Y) i Z nezavisne??? Puno hvala!! |
novija verzija knjige, zadatak 18, str. 165
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
|






