| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
dr.gonzo
Forumaš(ica)


Pridružen/a: 09. 09. 2005. (15:12:13)
Postovi: (7)16
|
 Postano: 16:18 čet, 29. 9. 2005 Naslov: Postano: 16:18 čet, 29. 9. 2005 Naslov: |
    |
|
|
Pa, ukoliko nisam negdje pogrijesio, rekao bih da ne vrijedi...
Uglavnom zbog toga sto u Q ne vrijedi nesto poput Leme: "Svaki omeden monoton niz konvergira" (sto vrijedi u R)
Npr. uzmimo niz decimalnih aproksimacija broja [latex]\pi[/latex] u Q (primjer iz knjige Cauchyjevog nekonvergentnog niza u Q)
On dakle nema limes u Q, ali ima u R. To znaci da i svaki njegov podniz ima limes u R i to taj isti (dakle [latex]\pi[/latex] (zbog TM4.5)). No to znaci da nema limes u Q (kad bi imao limes u Q to bi ujedno bio i limes u R, pa bi imao 2 razlicita limesa u R)
Imamo dakle, ogranicen niz u Q ciji nijedan podniz nije konvergentan u Q, tj. koji nema gomilista.
Nadam se da sam bio jasan :D
Pa, ukoliko nisam negdje pogrijesio, rekao bih da ne vrijedi...
Uglavnom zbog toga sto u Q ne vrijedi nesto poput Leme: "Svaki omeden monoton niz konvergira" (sto vrijedi u R)
Npr. uzmimo niz decimalnih aproksimacija broja  u Q (primjer iz knjige Cauchyjevog nekonvergentnog niza u Q) u Q (primjer iz knjige Cauchyjevog nekonvergentnog niza u Q)
On dakle nema limes u Q, ali ima u R. To znaci da i svaki njegov podniz ima limes u R i to taj isti (dakle  (zbog TM4.5)). No to znaci da nema limes u Q (kad bi imao limes u Q to bi ujedno bio i limes u R, pa bi imao 2 razlicita limesa u R) (zbog TM4.5)). No to znaci da nema limes u Q (kad bi imao limes u Q to bi ujedno bio i limes u R, pa bi imao 2 razlicita limesa u R)
Imamo dakle, ogranicen niz u Q ciji nijedan podniz nije konvergentan u Q, tj. koji nema gomilista.
Nadam se da sam bio jasan 
_________________
BEWARE
Today: the Doctor
Tomorrow: You
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
|
| [Vrh] |
|
dr.gonzo
Forumaš(ica)


Pridružen/a: 09. 09. 2005. (15:12:13)
Postovi: (7)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 12:14 pon, 3. 10. 2005 Naslov: Postano: 12:14 pon, 3. 10. 2005 Naslov: |
    |
|
|
Teorem kaze da svaki beskonacni, omedjeni podskup od [latex]\mathbb{R}^n[/latex] ima gomiliste. :)
[url=http://mathworld.wolfram.com/Bolzano-WeierstrassTheorem.html]Dokaz[/url] se temelji na potpunosti od [latex]\mathbb{R}^n[/latex]. :-s Dakle, kad bi pokusali na [latex]\mathbb{Q}^n[/latex], dokaz ne bi prosao. :(
Primjer koji je dr.gonzo dao je, po meni, ok. 8) Skup [i]S[/i] navedenih aproksimacija broja [latex]\pi[/latex] stvarno [b]je[/b] beskonacan (prebrojiv) i ogranicen. :)
Pogledajmo zasto dokaz teorema "pada" u slucaju kad se igramo s [latex]\mathbb{Q}[/latex]: da li je [i]S[/i] i zatvoren? :-k Neka je [latex]S' := \mathbb{Q} \setminus S[/latex]. :) Lako je pokazati da oko svake tocke iz [i]S'[/i] imamo otvorenu okolinu koja ne sadrzi tocke iz [i]S[/i], tj. koja je podskup od [i]S'[/i] :arrow: [i]S'[/i] je otvoren, pa je [i]S[/i] zatvoren. 8) A nema gomiliste u [latex]\mathbb{Q}[/latex] (naravno, ima u [latex]\mathbb{R}[/latex], sto nam i BW teorem kaze). 8)
Teorem kaze da svaki beskonacni, omedjeni podskup od  ima gomiliste. ima gomiliste. 
Dokaz se temelji na potpunosti od  . .  Dakle, kad bi pokusali na Dakle, kad bi pokusali na 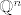 , dokaz ne bi prosao. , dokaz ne bi prosao. 
Primjer koji je dr.gonzo dao je, po meni, ok.  Skup S navedenih aproksimacija broja Skup S navedenih aproksimacija broja  stvarno je beskonacan (prebrojiv) i ogranicen. stvarno je beskonacan (prebrojiv) i ogranicen. 
Pogledajmo zasto dokaz teorema "pada" u slucaju kad se igramo s 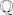 : da li je S i zatvoren? : da li je S i zatvoren?  Neka je Neka je  . .  Lako je pokazati da oko svake tocke iz S' imamo otvorenu okolinu koja ne sadrzi tocke iz S, tj. koja je podskup od S' Lako je pokazati da oko svake tocke iz S' imamo otvorenu okolinu koja ne sadrzi tocke iz S, tj. koja je podskup od S'  S' je otvoren, pa je S zatvoren. S' je otvoren, pa je S zatvoren.  A nema gomiliste u A nema gomiliste u 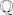 (naravno, ima u (naravno, ima u  , sto nam i BW teorem kaze). , sto nam i BW teorem kaze). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
dr.gonzo
Forumaš(ica)


Pridružen/a: 09. 09. 2005. (15:12:13)
Postovi: (7)16
|
 Postano: 13:28 pon, 3. 10. 2005 Naslov: Postano: 13:28 pon, 3. 10. 2005 Naslov: |
    |
|
|
[quote="vsego"]Teorem kaze da svaki beskonacni, omedjeni podskup od [latex]\mathbb{R}^n[/latex] ima gomiliste. :)[/quote]
Zapravo, teorem iz knjige prof. Ungara je Bolzano-Weierstrassov teorem za nizove, koji kaze:
"Svaki ograden niz [latex]{(P_k)}_k[/latex] u [latex]\mathbb{R}^n[/latex] ima gomiliste."
Napominjem ovo jer sam prvo pomislio da je ovo mozda specijalni slucaj teorema gore (tj. da se lako pokaze iz njega preko skupa vrijednosti niza), ali kako gomiliste niza i gomiliste skupa nisu bas isti pokaze se da npr. za niz (odnosno skup vrijednosti niza):
[latex]P_k={(-1)^k}[/latex]
teorem kojeg je naveo vsego ne govori nista (skup vrijednosti je konacan), dok tm za nizove govori da postoji gomiliste (u ovom slucaju dva gomilista -1 i 1).
Iako bi se, mozda, tm za nizove mogao dokazati iz prethodnog rastavljanjem na slucajeve kada je skup vrijednosti niza konacan odnosno beskonacan... ali nisam bas siguran jer i dalje ostaje pitanje razlike gomilista skupa i niza... :?
| vsego (napisa): | Teorem kaze da svaki beskonacni, omedjeni podskup od  ima gomiliste. ima gomiliste.  |
Zapravo, teorem iz knjige prof. Ungara je Bolzano-Weierstrassov teorem za nizove, koji kaze:
"Svaki ograden niz 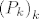 u u  ima gomiliste." ima gomiliste."
Napominjem ovo jer sam prvo pomislio da je ovo mozda specijalni slucaj teorema gore (tj. da se lako pokaze iz njega preko skupa vrijednosti niza), ali kako gomiliste niza i gomiliste skupa nisu bas isti pokaze se da npr. za niz (odnosno skup vrijednosti niza):

teorem kojeg je naveo vsego ne govori nista (skup vrijednosti je konacan), dok tm za nizove govori da postoji gomiliste (u ovom slucaju dva gomilista -1 i 1).
Iako bi se, mozda, tm za nizove mogao dokazati iz prethodnog rastavljanjem na slucajeve kada je skup vrijednosti niza konacan odnosno beskonacan... ali nisam bas siguran jer i dalje ostaje pitanje razlike gomilista skupa i niza... 
_________________
BEWARE
Today: the Doctor
Tomorrow: You
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 19:46 pon, 3. 10. 2005 Naslov: Postano: 19:46 pon, 3. 10. 2005 Naslov: |
    |
|
|
Onda se to zove BW za nizove. 8)
[quote="dr.gonzo"]Iako bi se, mozda, tm za nizove mogao dokazati iz prethodnog rastavljanjem na slucajeve kada je skup vrijednosti niza konacan odnosno beskonacan... ali nisam bas siguran jer i dalje ostaje pitanje razlike gomilista skupa i niza... :?[/quote]
Dakle, teorem opet kaze [b]za sve[/b] nizove. :D
Naravno da postoji konvergentan podniz i da je limes u tom skupu ako je skup slika konacan, jer to znaci da u bar jednu tocku skupa slika mora uletjeti beskonacno mnogo elemenata niza, sto je onda i gomiliste niza. :D Za to ti netrebaju nikakvi pametni teoremi, ne? ;)
Onda se to zove BW za nizove. 
| dr.gonzo (napisa): | Iako bi se, mozda, tm za nizove mogao dokazati iz prethodnog rastavljanjem na slucajeve kada je skup vrijednosti niza konacan odnosno beskonacan... ali nisam bas siguran jer i dalje ostaje pitanje razlike gomilista skupa i niza...  |
Dakle, teorem opet kaze za sve nizove. 
Naravno da postoji konvergentan podniz i da je limes u tom skupu ako je skup slika konacan, jer to znaci da u bar jednu tocku skupa slika mora uletjeti beskonacno mnogo elemenata niza, sto je onda i gomiliste niza.  Za to ti netrebaju nikakvi pametni teoremi, ne? Za to ti netrebaju nikakvi pametni teoremi, ne? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
|







