| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
 Postano: 18:34 ned, 27. 11. 2005 Naslov: definicija bidual ?? Postano: 18:34 ned, 27. 11. 2005 Naslov: definicija bidual ?? |
    |
|
|
[i]Gledam ovu definiciju i nikak da skužim o čemu se radi.[/i]
[b]Def. [/b] [latex]x \in V, f \in V'[/latex] definiramo funkciju [latex]\hat{x}:V' \rightarrow F[/latex] na slijedeći način: [latex]\hat{x}(f):= <x,f> = f(x), (\hat{x}\in V'') [/latex], time smo definirali funkciju [latex]\varphi:V \rightarrow V'', \varphi(x)=\hat{x} [/latex]. [latex] V'' [/latex] je bidual od [latex] V [/latex].
[i]Kužim da bi V'' trebao biti dualni prostor od V', ali nikako mi nije jasno ako je [latex]\hat{x}(f) := <x,f> = f(x)[/latex] pa kaj nije to onda potpuno ista stvar zapisana na drugi način :shock: . Uopće ne kužim kaj je tu novog definirano?
Ako se nađe neka dobra duša da prosvijetli mene blesavog bio bih joj jako zahvalan :pray:[/i]
Gledam ovu definiciju i nikak da skužim o čemu se radi.
Def. 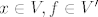 definiramo funkciju definiramo funkciju 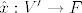 na slijedeći način: na slijedeći način: 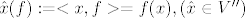 , time smo definirali funkciju , time smo definirali funkciju 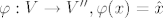 . . 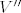 je bidual od je bidual od 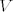 . .
Kužim da bi V'' trebao biti dualni prostor od V', ali nikako mi nije jasno ako je 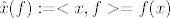 pa kaj nije to onda potpuno ista stvar zapisana na drugi način pa kaj nije to onda potpuno ista stvar zapisana na drugi način  . Uopće ne kužim kaj je tu novog definirano? . Uopće ne kužim kaj je tu novog definirano?
Ako se nađe neka dobra duša da prosvijetli mene blesavog bio bih joj jako zahvalan 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 19:20 ned, 27. 11. 2005 Naslov: Postano: 19:20 ned, 27. 11. 2005 Naslov: |
    |
|
|
Mi zelimo definirati funkciju (za koju cemo kasnije pokazati da je izomorfizam) [latex]\varphi \colon V \to V''[/latex]
Uzmimo, dakle neki element domene: [latex]x \in V[/latex].
Njemu cemo pridruziti [latex]\hat{x} \in V''[/latex].
Definiramo [latex]\hat{x} \colon V' \to \mathbb{F}[/latex] ovako:
Za [latex]f \in V'[/latex] (dakle [latex]f \colon V \to \mathbb{F}[/latex]) definiramo [latex]\hat{x}(f) := f(x)[/latex]
Uocimo da je [latex]\hat{x}[/latex] linearan funkcional, pa je prema tome sa [latex]\varphi(x) := \hat{x}[/latex] dobro definirana funkcija [latex]\varphi \colon V \to V''[/latex].
Nadam se da je sada jasnije.
Onaj [latex]<x,f>[/latex] mi stvarno nije jasan, jer je [latex]x\in V[/latex], a [latex]f \in V'[/latex]. Odakle ti to?
Mi zelimo definirati funkciju (za koju cemo kasnije pokazati da je izomorfizam) 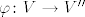
Uzmimo, dakle neki element domene: 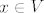 . .
Njemu cemo pridruziti  . .
Definiramo 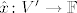 ovako: ovako:
Za 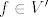 (dakle (dakle 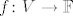 ) definiramo ) definiramo 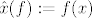
Uocimo da je 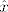 linearan funkcional, pa je prema tome sa linearan funkcional, pa je prema tome sa 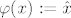 dobro definirana funkcija dobro definirana funkcija 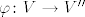 . .
Nadam se da je sada jasnije.
Onaj 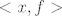 mi stvarno nije jasan, jer je mi stvarno nije jasan, jer je 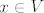 , a , a 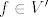 . Odakle ti to? . Odakle ti to?
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 19:34 ned, 27. 11. 2005 Naslov: Postano: 19:34 ned, 27. 11. 2005 Naslov: |
    |
|
|
[quote="venovako"]@mdoko:
Mozda se misli na teorem o reprezentaciji linearnih funkcionala, pa je [latex]f(x)[/latex] efektivno skalarni produkt [latex]x[/latex]-a sa (za dani funkcional [latex]f\in V'[/latex] jedinstvenim) vektorom, kojeg, zasto ne, opet nazovemo [latex]f[/latex] ([latex]\in V[/latex]).
Ali to mi izgleda kao pretjerana petljavina.[/quote]
Moguce, ali to je stvarno pretjerana petljavina. Takodjer stvara dodatnu zabunu kada se vidi po prvi put.
| venovako (napisa): | @mdoko:
Mozda se misli na teorem o reprezentaciji linearnih funkcionala, pa je 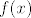 efektivno skalarni produkt efektivno skalarni produkt  -a sa (za dani funkcional -a sa (za dani funkcional 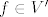 jedinstvenim) vektorom, kojeg, zasto ne, opet nazovemo jedinstvenim) vektorom, kojeg, zasto ne, opet nazovemo  ( (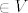 ). ).
Ali to mi izgleda kao pretjerana petljavina. |
Moguce, ali to je stvarno pretjerana petljavina. Takodjer stvara dodatnu zabunu kada se vidi po prvi put.
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
 Postano: 21:20 ned, 27. 11. 2005 Naslov: Postano: 21:20 ned, 27. 11. 2005 Naslov: |
    |
|
|
[quote="mdoko"]Mi zelimo definirati funkciju (za koju cemo kasnije pokazati da je izomorfizam) [latex]\varphi \colon V \to V''[/latex]
Uzmimo, dakle neki element domene: [latex]x \in V[/latex].
Njemu cemo pridruziti [latex]\hat{x} \in V''[/latex].
Definiramo [latex]\hat{x} \colon V' \to \mathbb{F}[/latex] ovako:
Za [latex]f \in V'[/latex] (dakle [latex]f \colon V \to \mathbb{F}[/latex]) definiramo [latex]\hat{x}(f) := f(x)[/latex]
Uocimo da je [latex]\hat{x}[/latex] linearan funkcional, pa je prema tome sa [latex]\varphi(x) := \hat{x}[/latex] dobro definirana funkcija [latex]\varphi \colon V \to V''[/latex].
Nadam se da je sada jasnije.
[/quote]
hmm..je malo jasnije. dal to sad znači da je [latex]\varphi(x)(f) = \hat{x}(f) [/latex] ?
ako je [latex] \hat{x}\in V''[/latex] zar nemamo onda odmah [latex]V''[/latex] kao skup svih takvih funkcionala i nazovemo ga bidualni prostor od [latex]V[/latex] . zašto nam treba [latex]\varphi [/latex] ??
[quote="mdoko"]
Onaj [latex]<x,f>[/latex] mi stvarno nije jasan, jer je [latex]x\in V[/latex], a [latex]f \in V'[/latex]. Odakle ti to?[/quote]
ma iz definicije od prije...neda mi se sad pisat, al to nije ni bitno kod ovog
| mdoko (napisa): | Mi zelimo definirati funkciju (za koju cemo kasnije pokazati da je izomorfizam) 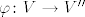
Uzmimo, dakle neki element domene: 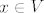 . .
Njemu cemo pridruziti  . .
Definiramo 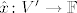 ovako: ovako:
Za 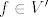 (dakle (dakle 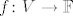 ) definiramo ) definiramo 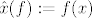
Uocimo da je 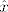 linearan funkcional, pa je prema tome sa linearan funkcional, pa je prema tome sa 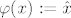 dobro definirana funkcija dobro definirana funkcija 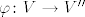 . .
Nadam se da je sada jasnije.
|
hmm..je malo jasnije. dal to sad znači da je 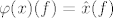 ? ?
ako je  zar nemamo onda odmah zar nemamo onda odmah 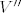 kao skup svih takvih funkcionala i nazovemo ga bidualni prostor od kao skup svih takvih funkcionala i nazovemo ga bidualni prostor od 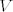 . zašto nam treba . zašto nam treba 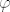 ?? ??
| mdoko (napisa): |
Onaj 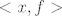 mi stvarno nije jasan, jer je mi stvarno nije jasan, jer je 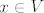 , a , a 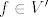 . Odakle ti to? . Odakle ti to? |
ma iz definicije od prije...neda mi se sad pisat, al to nije ni bitno kod ovog
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
 Postano: 9:58 pon, 28. 11. 2005 Naslov: Postano: 9:58 pon, 28. 11. 2005 Naslov: |
    |
|
|
Oznaka < x,f> = f(x).
< , > je bilinearni funkcional na VxV' (i nedegeneriran :)
Ta oznaka naglašava da je f(x) linearno i po f, i po x, i daje više ravnopravnosti f-u i x-u, što se upravo vidi kod izomorfnosti V i V''.
Naravno, ovo sve izgleda vrlo komplicirano za iste stvari: V, V' i V'' su izomorfni, ali to vrijedi samo za KONAČNODIMENZIONALNE prostore.
Općenito, V' nisu svi, nego svi NEPREKINUTI linearni funkcionali na recimo normiranom prostoru, i tada V izomorfno V'' vrijedi samo ponekad (refleksivni prostori), koji imaju posebna svojstva ...
Na konačnodimenzionalnom prostoru svaki linearni funkcional je neprekinut, pa je ono što smo radili točno, premda zamalo trivijalno.
- Nenad Antonić
Oznaka < x,f> = f(x).
< , > je bilinearni funkcional na VxV' (i nedegeneriran 
Ta oznaka naglašava da je f(x) linearno i po f, i po x, i daje više ravnopravnosti f-u i x-u, što se upravo vidi kod izomorfnosti V i V''.
Naravno, ovo sve izgleda vrlo komplicirano za iste stvari: V, V' i V'' su izomorfni, ali to vrijedi samo za KONAČNODIMENZIONALNE prostore.
Općenito, V' nisu svi, nego svi NEPREKINUTI linearni funkcionali na recimo normiranom prostoru, i tada V izomorfno V'' vrijedi samo ponekad (refleksivni prostori), koji imaju posebna svojstva ...
Na konačnodimenzionalnom prostoru svaki linearni funkcional je neprekinut, pa je ono što smo radili točno, premda zamalo trivijalno.
- Nenad Antonić
|
|
| [Vrh] |
|
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
|
| [Vrh] |
|
|







