| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ivo34
Forumaš(ica)


Pridružen/a: 03. 02. 2005. (10:11:04)
Postovi: (171)16
Spol: 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
ivo34
Forumaš(ica)


Pridružen/a: 03. 02. 2005. (10:11:04)
Postovi: (171)16
Spol: 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 17:14 pon, 28. 11. 2005 Naslov: Postano: 17:14 pon, 28. 11. 2005 Naslov: |
    |
|
|
[quote="ivo34"]Mislim da sam te shvatio, jel bi onda rjesenje
bilo ovak nesto:
12 + 22/(2-n^(1/n)) + 12/(2-n^(2/n)) + 2/(2-n^(3/n))
Jel mi tocno ovo rjesenje? :?:
[/quote]
:shock: :shock: :shock: :shock: :shock:
Kako ti rjesenje moze ostati u terminima od n? Promisli, sto bi taj n tu trebao znaciti?
Inace rjesenje je 96. (Nisam rjesavao rucno rijesila Mathematica 5).
Dakle ovako:
Oznacimo [latex]f(x) = \frac{1}{1-x} = \sum_{n=0}^\infty x^n[/latex]
Sada ocito vrijedi: [latex]
\sum_{n=0}^\infty \frac{1}{2^n} = f(\frac{1}{2}) = 2\ (*)
[/latex]
[latex]
f'(x) = \frac{1}{(1-x)^2} = \sum_{n=0}^\infty n x^{n-1}
[/latex]
Definirajmo funkciju g ovako:
[latex]
g(x) = xf'(x) = \frac{x}{(1-x)^2} = \sum_{n=0}^\infty n x^n
[/latex]
I uocimo:
[latex]
\sum_{n=0}^\infty \frac{n}{2^n} = g(\frac{1}{2}) = 2\ (**)
[/latex]
[latex]
g'(x) = \frac{1}{(1-x)^2} + \frac{2x}{(1-x)^3} = \sum_{n=0}^\infty n^2 x^{n-1}
[/latex]
Kao i gore definirajmo h:
[latex]
h(x) = xg'(x) = \frac{x}{(1-x)^2} + \frac{2x^2}{(1-x)^3} = \sum_{n=0}^\infty n^2 x^{n}
[/latex]
Odakle ponovno vidimo:
[latex]
\sum_{n=0}^\infty \frac{n^2}{2^n} = h(\frac{1}{2}) = 6\ (***)
[/latex]
Analogno kao i gore dobijemo (molim pitanje ako ovo nije jasno):
[latex]
\sum_{n=0}^\infty \frac{n^3}{2^n} = \frac{1}{2} h'(\frac{1}{2}) = 26\ (****)
[/latex]
Sada, koristeci rezultate oznacene s (*), (**), (***) i (****) dobijemo:
[latex]
6\sum_{n=0}^\infty\frac{1}{2^n}+11\sum_{n=0}^\infty\frac{n}{2^n}+6\sum_{n=0}^\infty\frac{n^2}{2^n}+\sum_{n=0}^\infty\frac{n^3}{2^n} = 96
[/latex]
Da li je sada jasno kako se ovo rjesava i zasto sve ovo vrijedi.
[quote]
Krivo sam se bio izrazio za d'Alamberta :roll: , nisam dobio
da konvergira u 1/2, nego da je [color=red]limes n+1 reda kroz
n red jednak 1/2,[/color] sto nam govori da red konvergira.
Nadam se da je to tocno? :)[/quote]
:ccc:
Valjda si mislio "limes od (n+1 [b]clan[/b] reda)/( n-ti [b]clan[/b] reda)"
Edit: typo
| ivo34 (napisa): | Mislim da sam te shvatio, jel bi onda rjesenje
bilo ovak nesto:
12 + 22/(2-n^(1/n)) + 12/(2-n^(2/n)) + 2/(2-n^(3/n))
Jel mi tocno ovo rjesenje? 
|
    
Kako ti rjesenje moze ostati u terminima od n? Promisli, sto bi taj n tu trebao znaciti?
Inace rjesenje je 96. (Nisam rjesavao rucno rijesila Mathematica 5).
Dakle ovako:
Oznacimo 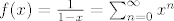
Sada ocito vrijedi: 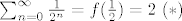
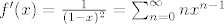
Definirajmo funkciju g ovako:
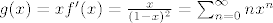
I uocimo:
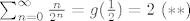
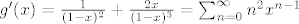
Kao i gore definirajmo h:
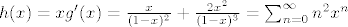
Odakle ponovno vidimo:
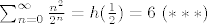
Analogno kao i gore dobijemo (molim pitanje ako ovo nije jasno):
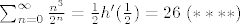
Sada, koristeci rezultate oznacene s (*), (**), (***) i (****) dobijemo:
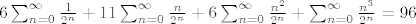
Da li je sada jasno kako se ovo rjesava i zasto sve ovo vrijedi.
| Citat: |
Krivo sam se bio izrazio za d'Alamberta  , nisam dobio , nisam dobio
da konvergira u 1/2, nego da je limes n+1 reda kroz
n red jednak 1/2, sto nam govori da red konvergira.
Nadam se da je to tocno?  |

Valjda si mislio "limes od (n+1 clan reda)/( n-ti clan reda)"
Edit: typo
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
Zadnja promjena: mdoko; 20:47 pon, 28. 11. 2005; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ivo34
Forumaš(ica)


Pridružen/a: 03. 02. 2005. (10:11:04)
Postovi: (171)16
Spol: 
|
 Postano: 20:44 pon, 28. 11. 2005 Naslov: Postano: 20:44 pon, 28. 11. 2005 Naslov: |
    |
|
|
OK, mislim da sam sad stvarno skuzio, jedino mi nije
jasna ona zadnja suma, sta ne bi trebalo bit suma n^3/2^n,
ti si napisao n^2/2^n? Inace, ideja je i za tu zadnju sumu
izderivirati h, definirat novu f-ju sa x*h'(x) i uvrstit 1/2, jel
tako?
Inace, hvala PUNO na ulozenom trudu jer si i jednom dibidusu
za redove kao sto sam ja uspio objasnit neke stvari. 8) :D
OK, mislim da sam sad stvarno skuzio, jedino mi nije
jasna ona zadnja suma, sta ne bi trebalo bit suma n^3/2^n,
ti si napisao n^2/2^n? Inace, ideja je i za tu zadnju sumu
izderivirati h, definirat novu f-ju sa x*h'(x) i uvrstit 1/2, jel
tako?
Inace, hvala PUNO na ulozenom trudu jer si i jednom dibidusu
za redove kao sto sam ja uspio objasnit neke stvari.  
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
ivo34
Forumaš(ica)


Pridružen/a: 03. 02. 2005. (10:11:04)
Postovi: (171)16
Spol: 
|
|
| [Vrh] |
|
|











