| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 0:10 sri, 30. 11. 2005 Naslov: Postano: 0:10 sri, 30. 11. 2005 Naslov: |
    |
|
|
[latex]F_n = \frac{(1+\sqrt{5})^n - (1-\sqrt{5})^n}{2^n\sqrt{5}}[/latex]
Provjeris za n=0,1 i pretpostavis da vrijedi za sve <= n. :) Provjeravamo za n+1:
[latex]$\begin{align*}
F_{n+1} &= F_n + F_{n-1} \\
&= \frac{(1+\sqrt{5})^n - (1-\sqrt{5})^n}{2^n\sqrt{5}} + \frac{(1+\sqrt{5})^{n-1} - (1-\sqrt{5})^{n-1}}{2^{n-1}\sqrt{5}} \\
&= \frac{(1+\sqrt{5})^n - (1-\sqrt{5})^n}{2^n\sqrt{5}} + \frac{2(1+\sqrt{5})^{n-1} - 2(1-\sqrt{5})^{n-1}}{2^n\sqrt{5}} \\
&= \frac{(1+\sqrt{5})^n - (1-\sqrt{5})^n+2(1+\sqrt{5})^{n-1} - 2(1-\sqrt{5})^{n-1}}{2^n\sqrt{5}} \\
&= \frac{(1+\sqrt{5})^{n-1}((1+\sqrt{5})+2) - (1-\sqrt{5})^{n-1}((1-\sqrt{5})+2)}{2^n\sqrt{5}} \\
&= \frac{(1+\sqrt{5})^{n-1}(3+\sqrt{5}) - (1-\sqrt{5})^{n-1}(3-\sqrt{5})}{2^n\sqrt{5}}
\end{align*}$[/latex]
Primijeti:
[latex](1\pm\sqrt{5})^2 = 1 \pm2\sqrt{5} + 5 = 6 \pm2\sqrt{5} = 2(3\pm\sqrt{5})[/latex]
Dakle:
[latex]$\begin{align*}
F_{n+1} &= \frac{2^{-1}(1+\sqrt{5})^{n-1}(1+\sqrt{5})^2 - 2^{-1}(1-\sqrt{5})^{n-1}(1-\sqrt{5})^2}{2^n\sqrt{5}} \\
&= \frac{(1+\sqrt{5})^{n+1} - (1-\sqrt{5})^{n+1}}{2^{n+1}\sqrt{5}}
\end{align*}$[/latex]
Inace, zdravije je da napises [b]sto[/b] si radio, nego da cekas da ti netko rijesi "od nule"... ;)
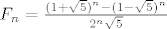
Provjeris za n=0,1 i pretpostavis da vrijedi za sve ⇐ n.  Provjeravamo za n+1: Provjeravamo za n+1:
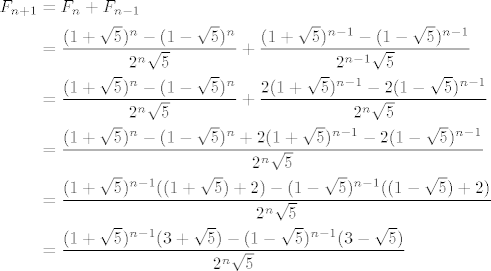
Primijeti:
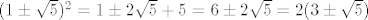
Dakle:
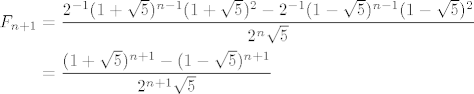
Inace, zdravije je da napises sto si radio, nego da cekas da ti netko rijesi "od nule"... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 0:26 sri, 30. 11. 2005 Naslov: Postano: 0:26 sri, 30. 11. 2005 Naslov: |
    |
|
|
[quote="vsego"]
[latex]$\begin{align*}
F_{n+1} &= \frac{2^{-1}(1+\sqrt{5})^{n-1}(1+\sqrt{5})^2 - 2^{-1}(1-\sqrt{5})^{n-1}(1-\sqrt{5})^2}{2^n\sqrt{5}} \\
&= \frac{(1+\sqrt{5})^{n+1} - (1-\sqrt{5})^{n+1}}{2^{n+1}\sqrt{5}}
\end{align*}$[/latex]
Inace, zdravije je da napises [b]sto[/b] si radio, nego da cekas da ti netko rijesi "od nule"... ;)[/quote]
E hvala ti prije svega!
Kada sam ja rješavao došao sam do istoga zaključka kao i ti, međutim ja sam išao iz binetove formule, pa dokazao da T(1) vrijedi, tada sam uvrstio za prvi slijedeći...i isto dobio (i ostao u sumnji)
Je li može tako?
(Ako ne kužiš što govorim pa da sliku ubacim (budući da latex ne znam).)
| vsego (napisa): |
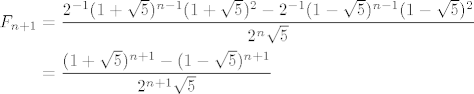
Inace, zdravije je da napises sto si radio, nego da cekas da ti netko rijesi "od nule"...  |
E hvala ti prije svega!
Kada sam ja rješavao došao sam do istoga zaključka kao i ti, međutim ja sam išao iz binetove formule, pa dokazao da T(1) vrijedi, tada sam uvrstio za prvi slijedeći...i isto dobio (i ostao u sumnji)
Je li može tako?
(Ako ne kužiš što govorim pa da sliku ubacim (budući da latex ne znam).)
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Lord R
Forumaš(ica)


Pridružen/a: 15. 11. 2005. (01:03:34)
Postovi: (5D)16
Spol: 
|
 Postano: 1:17 sri, 30. 11. 2005 Naslov: Postano: 1:17 sri, 30. 11. 2005 Naslov: |
    |
|
|
[quote="vsego"]To sam otprilike i ja napravio (samo raspisano). 8)
Ali pazi: [latex]F_n = \frac{(1+\sqrt{5})^n - (1-\sqrt{5})^n}{2^n\sqrt{5}}[/latex]
Dakle, [latex]F_n[/latex] ovisi o [latex]F_{n-1}[/latex] [size=19][color=red][b]i[/b][/color][/size] [latex]F_{n-2}[/latex] :arrow: bazu indukcije moras provjeriti za dvije vrijednosti (kako sam napisao: za 0 i 1). 8)[/quote]
Ahaaa, da i drugu bazu!!!
I ja sam bio prvi puta krenuo na tvoj način samo sam bio zapeo na rastavljanju, no sada je super,...cool, kužim sve i još jednom ti puno hvala!
| vsego (napisa): | To sam otprilike i ja napravio (samo raspisano). 
Ali pazi: 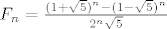
Dakle, 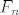 ovisi o ovisi o 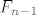 i i 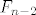  bazu indukcije moras provjeriti za dvije vrijednosti (kako sam napisao: za 0 i 1). bazu indukcije moras provjeriti za dvije vrijednosti (kako sam napisao: za 0 i 1).  |
Ahaaa, da i drugu bazu!!!
I ja sam bio prvi puta krenuo na tvoj način samo sam bio zapeo na rastavljanju, no sada je super,...cool, kužim sve i još jednom ti puno hvala!
|
|
| [Vrh] |
|
|










