| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gordan
Forumaš(ica)


Pridružen/a: 03. 11. 2002. (18:01:44)
Postovi: (192)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 23:17 čet, 15. 12. 2005 Naslov: Postano: 23:17 čet, 15. 12. 2005 Naslov: |
    |
|
|
Probat cu ovako jer ne znam ljepse...
[code:1]
e_1 e_7
V_1-------------V_2------------V_7
| |
|e_2 |e_8
| e_3 |
V_3-------------V_4
| |
| |
|e_4 |e_5
| e_6 |
V_5-------------V_6
[/code:1]
Za pocetak (korijen) uzmes bilo koji vrh. Recimo V_1
BFS
Pronades sve vrhove koji su bridom povezani s V_1. To su V_2 i V_3. Njih dodas u stablo(naravno zajedno s bridom koji povezuje vrh iz kojeg si trazio s vrhom kojeg si nasao). Sada trazis iz vrhova koje si nasao u proslom koraku - za V_2 trazis sve vrhove koji su bridom povezani sa njim, osim vrhova koji se vec nalaze u stablu (dakle V_1, V_2, V_3). To su V_4 i V_7, njih dodas u stablo. Za V_3 radis istu stvar i nades V_5 (V_4 je vec u stablu), njega takoder dodas u stablo. U zadnjem koraku si pronasao V_7, V_4 i V_5, pa iz njih trazis susjede koji jos nisu u stablu. iz V_7 ne vidis nista, iz V_4 nades V_6, iz V_5 ne nades nista. Njega takoder dodas u stablo. Nastavljas sa trazenjem iz vrhova koje si nasao u prethodnom koraku, a to je samo V_6, ali ne nalazis nijedan novi vrh, sto je znak za kraj algoritma.
Stablo koje si dobio izgleda ovako:
[code:1]
e_1 e_7
V_1-------------V_2------------V_7
| |
|e_2 |e_8
| |
V_3 V_4
| |
| |
|e_4 |e_5
| |
V_5 V_6
[/code:1]
DFS
Opet pocnes s V_1, trazis vrh koji mu je susjedan, nalazis V_2, dodajes ga u stablo i ides na V_2. Iz V_2 trazis susjedan koji nije u stablu, nalazis V_7, dodajes ga u stablo i ides na V_7. Iz V_7 ne nalazis nijedan susjedan vrh pa se vracas natrag na V_2. Trazis novi vrh iz V_2 i vidis V_4, dodas ga, i ides na V_4, iz V_4 vidis V_3, dodas ga i ides na V_3. Iz V_3 vidis V_5, dodas ga i ides na njega, iz njega vidis V_6, dodas ga i ides na njega. Iz V_6 ne vidis novi vrh pa se vracas na V_5, opet nema novog pa se vracas na V_3, pa na V_4, pa na V_2, pa na V_1. Iz V_1 takoder nema novog vrha, sto je znak za kraj algoritma (alternativno, ako unaprijed znas koliko vrhova moras imati u stablu, sto ces kad vidis graf ocito znati, znas da je gotovo cim dodas zadnji vrh)
Dobijes ovakvo stablo:
[code:1]
e_1 e_7
V_1-------------V_2------------V_7
|
|e_8
e_3 |
V_3-------------V_4
|
|
|e_4
| e_6
V_5-------------V_6
[/code:1]
Uglavnom BFS ti je, iako to mozda iz ovog primjera nije ocito, puno brzi i bolji od DFSa :)[/code]
Probat cu ovako jer ne znam ljepse...
| Kod: |
e_1 e_7
V_1-------------V_2------------V_7
| |
|e_2 |e_8
| e_3 |
V_3-------------V_4
| |
| |
|e_4 |e_5
| e_6 |
V_5-------------V_6
|
Za pocetak (korijen) uzmes bilo koji vrh. Recimo V_1
BFS
Pronades sve vrhove koji su bridom povezani s V_1. To su V_2 i V_3. Njih dodas u stablo(naravno zajedno s bridom koji povezuje vrh iz kojeg si trazio s vrhom kojeg si nasao). Sada trazis iz vrhova koje si nasao u proslom koraku - za V_2 trazis sve vrhove koji su bridom povezani sa njim, osim vrhova koji se vec nalaze u stablu (dakle V_1, V_2, V_3). To su V_4 i V_7, njih dodas u stablo. Za V_3 radis istu stvar i nades V_5 (V_4 je vec u stablu), njega takoder dodas u stablo. U zadnjem koraku si pronasao V_7, V_4 i V_5, pa iz njih trazis susjede koji jos nisu u stablu. iz V_7 ne vidis nista, iz V_4 nades V_6, iz V_5 ne nades nista. Njega takoder dodas u stablo. Nastavljas sa trazenjem iz vrhova koje si nasao u prethodnom koraku, a to je samo V_6, ali ne nalazis nijedan novi vrh, sto je znak za kraj algoritma.
Stablo koje si dobio izgleda ovako:
| Kod: |
e_1 e_7
V_1-------------V_2------------V_7
| |
|e_2 |e_8
| |
V_3 V_4
| |
| |
|e_4 |e_5
| |
V_5 V_6
|
DFS
Opet pocnes s V_1, trazis vrh koji mu je susjedan, nalazis V_2, dodajes ga u stablo i ides na V_2. Iz V_2 trazis susjedan koji nije u stablu, nalazis V_7, dodajes ga u stablo i ides na V_7. Iz V_7 ne nalazis nijedan susjedan vrh pa se vracas natrag na V_2. Trazis novi vrh iz V_2 i vidis V_4, dodas ga, i ides na V_4, iz V_4 vidis V_3, dodas ga i ides na V_3. Iz V_3 vidis V_5, dodas ga i ides na njega, iz njega vidis V_6, dodas ga i ides na njega. Iz V_6 ne vidis novi vrh pa se vracas na V_5, opet nema novog pa se vracas na V_3, pa na V_4, pa na V_2, pa na V_1. Iz V_1 takoder nema novog vrha, sto je znak za kraj algoritma (alternativno, ako unaprijed znas koliko vrhova moras imati u stablu, sto ces kad vidis graf ocito znati, znas da je gotovo cim dodas zadnji vrh)
Dobijes ovakvo stablo:
| Kod: |
e_1 e_7
V_1-------------V_2------------V_7
|
|e_8
e_3 |
V_3-------------V_4
|
|
|e_4
| e_6
V_5-------------V_6
|
Uglavnom BFS ti je, iako to mozda iz ovog primjera nije ocito, puno brzi i bolji od DFSa  [/code] [/code]
_________________
Bri
|
|
| [Vrh] |
|
Gordan
Forumaš(ica)


Pridružen/a: 03. 11. 2002. (18:01:44)
Postovi: (192)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 9:51 sub, 17. 12. 2005 Naslov: Postano: 9:51 sub, 17. 12. 2005 Naslov: |
    |
|
|
U biti, algoritam koji je bolje odabrati za pretraživanje ponekad ovisi o samoj prirodi problema. Recimo, ako znamo da se ono što tražimo nalazi "blizu" vrha koji nam je početni, bolje je odabrati BFS. Ako nam je bitno da je rješenje "najbliže" početnom vrhu, isto je bolje odabrati BFS.
Kao što ahri kaže, DFS je puno lakše iskodirati i ne troši previše memorije. BFS bi nam možda prije riješio problem, ali memorijski je zahtjevniji jer koristi queue za spremanje vrhova koje mora posjetiti.
I tako, svaki ima svoje prednosti i mane. Ako je svejedno koji se koristi, ja bih isto uvijek prije odabrao DFS nego BFS zbog jednostavnosti.
U biti, algoritam koji je bolje odabrati za pretraživanje ponekad ovisi o samoj prirodi problema. Recimo, ako znamo da se ono što tražimo nalazi "blizu" vrha koji nam je početni, bolje je odabrati BFS. Ako nam je bitno da je rješenje "najbliže" početnom vrhu, isto je bolje odabrati BFS.
Kao što ahri kaže, DFS je puno lakše iskodirati i ne troši previše memorije. BFS bi nam možda prije riješio problem, ali memorijski je zahtjevniji jer koristi queue za spremanje vrhova koje mora posjetiti.
I tako, svaki ima svoje prednosti i mane. Ako je svejedno koji se koristi, ja bih isto uvijek prije odabrao DFS nego BFS zbog jednostavnosti.
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 13:19 sub, 17. 12. 2005 Naslov: Postano: 13:19 sub, 17. 12. 2005 Naslov: |
    |
|
|
[quote="Grga"]Pa za to bi trebalo stvarno puno vrhova, recimo koji milijun.[/quote]
U praksi, to i nije puno... :shock:
Evo jedan primjer: u magisteriju imam graf s [latex]n^2[/latex] vrhova i [latex]2n^2 - n[/latex] bridova. :? Ako se doticni "ispravno" posloze, taj graf mi producira skup od otprilike [latex]O(n^n)[/latex] generatora konusa (nekakvi vektori u [latex](2n^2 - n)[/latex]-dimenzionalnom prostoru). :shock:
Nema nikakve veze s BSF/DSF; samo pokazuje kako brojevi u praksi jako lako narastu, pa milijun stvarno nije nesto... :?
| Grga (napisa): | | Pa za to bi trebalo stvarno puno vrhova, recimo koji milijun. |
U praksi, to i nije puno... 
Evo jedan primjer: u magisteriju imam graf s 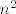 vrhova i vrhova i 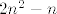 bridova. bridova.  Ako se doticni "ispravno" posloze, taj graf mi producira skup od otprilike Ako se doticni "ispravno" posloze, taj graf mi producira skup od otprilike 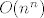 generatora konusa (nekakvi vektori u generatora konusa (nekakvi vektori u 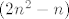 -dimenzionalnom prostoru). -dimenzionalnom prostoru). 
Nema nikakve veze s BSF/DSF; samo pokazuje kako brojevi u praksi jako lako narastu, pa milijun stvarno nije nesto... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 16:24 sub, 17. 12. 2005 Naslov: Postano: 16:24 sub, 17. 12. 2005 Naslov: |
    |
|
|
Pa dobro, što se tiče modeliranja kao predmeta, BFS i DFS se mogu smatrati algoritmima za generiranje stabla. Barem u ljudskom kompjuteru, mozgu, se mogu tako smatrati.
I tada ako mozak smatramo procesorom, tada BFS je stvarno brži u većini slučajeva. Neću reći u svim, jer možda postoji neki primjer gdje DFS brže izgenerira stablo, ali takav primjer nismo napravili na vježbama, niti sam ga ja vidio igdje drugdje. :)
Pa dobro, što se tiče modeliranja kao predmeta, BFS i DFS se mogu smatrati algoritmima za generiranje stabla. Barem u ljudskom kompjuteru, mozgu, se mogu tako smatrati.
I tada ako mozak smatramo procesorom, tada BFS je stvarno brži u većini slučajeva. Neću reći u svim, jer možda postoji neki primjer gdje DFS brže izgenerira stablo, ali takav primjer nismo napravili na vježbama, niti sam ga ja vidio igdje drugdje. 
_________________
The Dude Abides
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 15:08 ned, 18. 12. 2005 Naslov: Postano: 15:08 ned, 18. 12. 2005 Naslov: |
    |
|
|
[quote="vsego"][quote="Grga"]Pa za to bi trebalo stvarno puno vrhova, recimo koji milijun.[/quote]
U praksi, to i nije puno... :shock:
Evo jedan primjer: u magisteriju imam graf s [latex]n^2[/latex] vrhova i [latex]2n^2 - n[/latex] bridova. :? Ako se doticni "ispravno" posloze, taj graf mi producira skup od otprilike [latex]O(n^n)[/latex] generatora konusa (nekakvi vektori u [latex](2n^2 - n)[/latex]-dimenzionalnom prostoru). :shock:
Nema nikakve veze s BSF/DSF; samo pokazuje kako brojevi u praksi jako lako narastu, pa milijun stvarno nije nesto... :?[/quote]
Istina da mi je argument losh, ono sto sam trebao reci je:
Ako imamo n vrhova, a graf je jednostavan, mozemo imati [latex]\frac{n(n-1)}{2}[/latex] bridova.
Pa sad, ako smo imali memorije za n^2 bridova, queue od do n vrhova ne bi trebao biti tako problematican.
S druge strane, u rekurziji se stack overflow pojavljuje prilicno brzo, vec kod kojih 100-200 poziva u dubinu (iteracija, rekurzivnih poziva, ili kako god se to vec zove, ti izrazi mi nikad nisu isli :oops: ).
Mislim, ocito je da DFS necemu sluzi, jer inace ga se ne bi ni spominjalo (ocito se npr koristi u stvarnom zivotu, jer malo je teze uzivo primijeniti BFS :lol: npr. ako moramo pronaci izlaz iz labirinta :P), ali u svakom problemu koji meni pada na pamet, DFS je u najboljem slucaju jednako dobar kao BFS (osim ako imamo srece, ali to nije dobar argument :D).
@vili: Pa naravno da me ahri nije skuzio, kad ne zna moj nick na forumu, a nije tako lako povezati moj nick na forumu i onaj irl :P
Doduse, reakcija bi mi bila razumljivija da je znao da sam to ja, a ne da tako ismijava neku nepoznatu osobu, koja je, btw, samo htjela pomoci (ccc ahri) :shock:
| vsego (napisa): | | Grga (napisa): | | Pa za to bi trebalo stvarno puno vrhova, recimo koji milijun. |
U praksi, to i nije puno... 
Evo jedan primjer: u magisteriju imam graf s 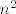 vrhova i vrhova i 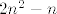 bridova. bridova.  Ako se doticni "ispravno" posloze, taj graf mi producira skup od otprilike Ako se doticni "ispravno" posloze, taj graf mi producira skup od otprilike 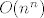 generatora konusa (nekakvi vektori u generatora konusa (nekakvi vektori u 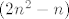 -dimenzionalnom prostoru). -dimenzionalnom prostoru). 
Nema nikakve veze s BSF/DSF; samo pokazuje kako brojevi u praksi jako lako narastu, pa milijun stvarno nije nesto...  |
Istina da mi je argument losh, ono sto sam trebao reci je:
Ako imamo n vrhova, a graf je jednostavan, mozemo imati 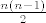 bridova. bridova.
Pa sad, ako smo imali memorije za n^2 bridova, queue od do n vrhova ne bi trebao biti tako problematican.
S druge strane, u rekurziji se stack overflow pojavljuje prilicno brzo, vec kod kojih 100-200 poziva u dubinu (iteracija, rekurzivnih poziva, ili kako god se to vec zove, ti izrazi mi nikad nisu isli  ). ).
Mislim, ocito je da DFS necemu sluzi, jer inace ga se ne bi ni spominjalo (ocito se npr koristi u stvarnom zivotu, jer malo je teze uzivo primijeniti BFS  npr. ako moramo pronaci izlaz iz labirinta npr. ako moramo pronaci izlaz iz labirinta  ), ali u svakom problemu koji meni pada na pamet, DFS je u najboljem slucaju jednako dobar kao BFS (osim ako imamo srece, ali to nije dobar argument ), ali u svakom problemu koji meni pada na pamet, DFS je u najboljem slucaju jednako dobar kao BFS (osim ako imamo srece, ali to nije dobar argument  ). ).
@vili: Pa naravno da me ahri nije skuzio, kad ne zna moj nick na forumu, a nije tako lako povezati moj nick na forumu i onaj irl 
Doduse, reakcija bi mi bila razumljivija da je znao da sam to ja, a ne da tako ismijava neku nepoznatu osobu, koja je, btw, samo htjela pomoci (ccc ahri) 
_________________
Bri
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
|


















