| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 12:52 ned, 18. 12. 2005 Naslov: Re: primjeri nizova Postano: 12:52 ned, 18. 12. 2005 Naslov: Re: primjeri nizova |
    |
|
|
[quote="Anonymous"]evo par pitanja iz nizova:
NAVEDITE PRIMJERE NIZOVA:
a)s 3 različita gomilišta u R
(jel to moze biti (An)=[n] mod 3 ) []-mi znači apsolutno
b)s 2 gomilišta u R i s još dva u R crtano
c)Postoji li niz s beskonačno mnogo gomilišta u R? A u R crtano? Svoje tvrdnje obrazložite
d) Mora li niz koji ima gomilište u R biti ograničen? obrazložite
Kolko ja znam R crtano je unija R i +i- beskonačno...
Unaprijed HVALA[/quote]
evo par odgovora na pitanja iz nizova
(a) Realan niz [latex](a_n)_n[/latex] zadan sa [latex]a_n:= \cos(n \pi/2)[/latex] ima točno tri gomilišta, [latex]-1,0,1[/latex]
I tvoj niz je dobar, tj. niz [latex](a_n)_n[/latex] definiran sa [latex]a_n:= (n \mod 3) [/latex] isto ima točno tri gomilišta, [latex]0,1,2[/latex].
(b) Realan niz [latex](a_n)_n[/latex] zadan sa [latex]a_n:= n \cdot(\cos (n \pi/2))+ (n \mod 4)[/latex] ima tražena svojstva, tj. skup gomilišta tog niza u [latex]\mathbb{\overline{R}}[/latex] je [latex]\{-\infty, 1,3, + \infty\}[/latex].
(c) Postoj, npr. bilo koja bijekcija [latex]\sigma : \mathbb{N} \rightarrow \mathbb{Q}[/latex]. Takva postoji i primjer jedne se može naći u skripti prof. Guljaša. Kako je [latex]\mathbb{Q}[/latex] gust u [latex]\mathbb{R}[/latex] (dokaz isto imate u istoj skripti), to za svako [latex] x \in \mathbb{R}[/latex] postoji podniz niza [latex](\sigma_n)_n[/latex] koji konvergira prema [latex]x[/latex]. Sprecijalno, takav niz ne može biti ograničen niti odozgo niti odozdo, pa su mu i [latex]-\infty[/latex] i [latex]+\infty[/latex] gomilišta. Drugim riječima skup gomilišta tog niza (u [latex]\mathbb{\overline{R}}[/latex]) je čitav [latex]\mathbb{\overline{R}}[/latex]
(d) Ne mora. Evo npr. radikalan (kontra)primjer takvog niza je onaj iz (c), taj očito nije ograničen, a svaki realni broj mu je gomilište.
E da, i u ovom kolegiju se definira [latex]\mathbb{\overline{R}}:=\mathbb{R}\cup \{-\infty, \infty\} [/latex]. :D
| Anonymous (napisa): | evo par pitanja iz nizova:
NAVEDITE PRIMJERE NIZOVA:
a)s 3 različita gomilišta u R
(jel to moze biti (An)=[n] mod 3 ) []-mi znači apsolutno
b)s 2 gomilišta u R i s još dva u R crtano
c)Postoji li niz s beskonačno mnogo gomilišta u R? A u R crtano? Svoje tvrdnje obrazložite
d) Mora li niz koji ima gomilište u R biti ograničen? obrazložite
Kolko ja znam R crtano je unija R i +i- beskonačno...
Unaprijed HVALA |
evo par odgovora na pitanja iz nizova
(a) Realan niz 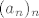 zadan sa zadan sa 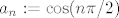 ima točno tri gomilišta, ima točno tri gomilišta, 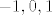
I tvoj niz je dobar, tj. niz 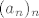 definiran sa definiran sa 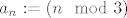 isto ima točno tri gomilišta, isto ima točno tri gomilišta, 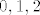 . .
(b) Realan niz 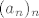 zadan sa zadan sa 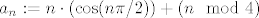 ima tražena svojstva, tj. skup gomilišta tog niza u ima tražena svojstva, tj. skup gomilišta tog niza u 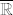 je je 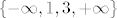 . .
(c) Postoj, npr. bilo koja bijekcija 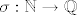 . Takva postoji i primjer jedne se može naći u skripti prof. Guljaša. Kako je . Takva postoji i primjer jedne se može naći u skripti prof. Guljaša. Kako je 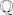 gust u gust u  (dokaz isto imate u istoj skripti), to za svako (dokaz isto imate u istoj skripti), to za svako 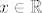 postoji podniz niza postoji podniz niza 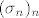 koji konvergira prema koji konvergira prema  . Sprecijalno, takav niz ne može biti ograničen niti odozgo niti odozdo, pa su mu i . Sprecijalno, takav niz ne može biti ograničen niti odozgo niti odozdo, pa su mu i 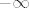 i i  gomilišta. Drugim riječima skup gomilišta tog niza (u gomilišta. Drugim riječima skup gomilišta tog niza (u 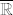 ) je čitav ) je čitav 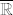
(d) Ne mora. Evo npr. radikalan (kontra)primjer takvog niza je onaj iz (c), taj očito nije ograničen, a svaki realni broj mu je gomilište.
E da, i u ovom kolegiju se definira 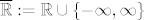 . . 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 17:43 ned, 18. 12. 2005 Naslov: Postano: 17:43 ned, 18. 12. 2005 Naslov: |
    |
|
|
[code:1]1/1 1/2 1/3 1/4 ...
2/1 2/2 2/3 2/4 ...
3/1 3/2 3/3 3/4 ...
...[/code:1]
Brojeve stavljas u niz po dijagonalama, preskacuci one koje si vec uzeo (ili one koji nisu do kraja "pokraceni):
1/1,2/1,1/2,3/1,(2/2 preskocis),1/3, 4/1, 3/2, 2/3, 1/4,... :D
| Kod: | 1/1 1/2 1/3 1/4 ...
2/1 2/2 2/3 2/4 ...
3/1 3/2 3/3 3/4 ...
... |
Brojeve stavljas u niz po dijagonalama, preskacuci one koje si vec uzeo (ili one koji nisu do kraja "pokraceni):
1/1,2/1,1/2,3/1,(2/2 preskocis),1/3, 4/1, 3/2, 2/3, 1/4,... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
FakEmaN
Forumaš(ica)

Pridružen/a: 18. 12. 2005. (17:28:59)
Postovi: (1)16
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
|








