| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
user
Forumaš(ica)

Pridružen/a: 30. 12. 2005. (01:04:08)
Postovi: (1)16
|
 Postano: 1:38 pet, 30. 12. 2005 Naslov: Zna li tko dokazati nejednakost??? Postano: 1:38 pet, 30. 12. 2005 Naslov: Zna li tko dokazati nejednakost??? |
    |
|
|
Pozdrav matematicari, zna li pliiiz itko dokazati ovo:
[latex] 2 (\vert {z_1}\vert^{n} + \vert {z_2}\vert ^n) \leq \vert z_1 + z_2 \vert ^n + \vert z_1 - z_2 \vert^n \leq 2^{n-1} (\vert z_1\vert ^n + \vert z_2 \vert ^n ) [/latex], za [latex]n \geq 2[/latex], [latex] z_1, z_2 \in C [/latex]
Prvu nejednakost sam uspio dokazati izravno za sve parne n, binomnim razvojem, ali za izravan dokaz mi podosta problema zadaju korijeni kad izraz treba dokazati za neparne potencije.
Induktivni dokaz mi se cini jos slozenijim, tako da ne znam sto jos pokusati. O drugoj nisam jos stigao razmisljati, ima li tko kakav savjet??? Pomagajte molim vas :)
Unaprijed puno fala :))
Pozdrav!!
Pozdrav matematicari, zna li pliiiz itko dokazati ovo:
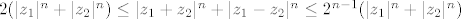 , za , za 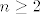 , , 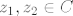
Prvu nejednakost sam uspio dokazati izravno za sve parne n, binomnim razvojem, ali za izravan dokaz mi podosta problema zadaju korijeni kad izraz treba dokazati za neparne potencije.
Induktivni dokaz mi se cini jos slozenijim, tako da ne znam sto jos pokusati. O drugoj nisam jos stigao razmisljati, ima li tko kakav savjet??? Pomagajte molim vas 
Unaprijed puno fala  ) )
Pozdrav!!
_________________
--
Goran
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 15:38 pon, 2. 1. 2006 Naslov: Postano: 15:38 pon, 2. 1. 2006 Naslov: |
    |
|
|
Jednom kad dokazes lijevu jednakost, onda samo uzmi supstituciju u=z1+z2, v=z1-z2 i napisi lijevu jednakost za njih i dobio si desnu. Dakle dovoljno ti je dokazati samo desnu.
Disclaimer: nisam raspisivala ovo nego samo nagadam: zar ne mozes neparne brojeve rijesiti isto kao i parne? Naime, ako su a i b oba pozitivni, onda je a<b ekvivalentno s a^2<b^2... Tako onda dobijes parne potencije. Doduse, pojavi ti se i onaj nesretni mjesoviti clan, ali mozda ako i njega raspises dobijes sto trebas?
Jednom kad dokazes lijevu jednakost, onda samo uzmi supstituciju u=z1+z2, v=z1-z2 i napisi lijevu jednakost za njih i dobio si desnu. Dakle dovoljno ti je dokazati samo desnu.
Disclaimer: nisam raspisivala ovo nego samo nagadam: zar ne mozes neparne brojeve rijesiti isto kao i parne? Naime, ako su a i b oba pozitivni, onda je a<b ekvivalentno s a^2<b^2... Tako onda dobijes parne potencije. Doduse, pojavi ti se i onaj nesretni mjesoviti clan, ali mozda ako i njega raspises dobijes sto trebas?
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 17:05 pon, 2. 1. 2006 Naslov: Postano: 17:05 pon, 2. 1. 2006 Naslov: |
    |
|
|
Za elegantno rješenje je korisno znati neke klasične nejednakosti. Navodim samo prikladne specijalne slučajeve, općenitije nejednakosti se mogu naći recimo u knjižici: Pečarić: "Nejednakosti".
[size=7]I ne, ja se ne bavim nejednakostima, samo ove stvari smatram općom kulturom. Ovo je upućeno potencijalnim zlobnicima, ostali nek zanemare.[/size]
Neka su a,b>=0 te 0<r<s.
[b]Nejednakost za potencijalne sredine[/b] (općenitije u "Nejednakosti", str. 39.)
[latex]\left(\displaystyle\frac{a^r+b^r}{2}\right)^{1/r}\leq\left(\displaystyle\frac{a^s+b^s}{2}\right)^{1/s}[/latex]
[b]Nejednakost za potencijalne sume[/b] (općenitije u "Nejednakosti", str. 36.)
[latex]\left(a^r+b^r\right)^{1/r}\geq\left(a^s+b^s\right)^{1/s}[/latex]
Dokažimo lijevu nejednakost.
Prije svega, lako se dokaže sljedeća jednakost (tzv. jednakost paralelograma), npr. direktnim raspisivanjem:
[latex]|z_1+z_2|^2+|z_1-z_2|^2=2(|z_1|^2+|z_2|^2)[/latex]
Sada iskoristimo NZPsredine uz r=2, s=n, zatim upotrijebimo gornju jednakost te konačno iskoristimo NZPsume uz r=2, s=n:
[latex]\left(\displaystyle\frac{|z_1+z_2|^n+|z_1-z_2|^n}{2}\right)^{1/n}\geq\left(\displaystyle\frac{|z_1+z_2|^2+|z_1-z_2|^2}{2}\right)^{1/2}=\\=\left(|z_1|^2+|z_2|^2\right)^{1/2}\geq\left(|z_1|^n+|z_2|^n\right)^{1/n}[/latex]
Preostaje sve dignuti na n-tu i pomnožiti s 2.
Desna nejednakost se dobije iz lijeve kako reče Martinab.
Ako nešto ipak treba detaljnije raspisati, samo pitaj. Nadam se da ovo nije neki "dječji" zadačić pa sam bezveze zakomplicirao. :lol:
Za elegantno rješenje je korisno znati neke klasične nejednakosti. Navodim samo prikladne specijalne slučajeve, općenitije nejednakosti se mogu naći recimo u knjižici: Pečarić: "Nejednakosti".
I ne, ja se ne bavim nejednakostima, samo ove stvari smatram općom kulturom. Ovo je upućeno potencijalnim zlobnicima, ostali nek zanemare.
Neka su a,b>=0 te 0<r<s.
Nejednakost za potencijalne sredine (općenitije u "Nejednakosti", str. 39.)
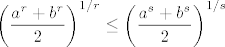
Nejednakost za potencijalne sume (općenitije u "Nejednakosti", str. 36.)
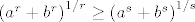
Dokažimo lijevu nejednakost.
Prije svega, lako se dokaže sljedeća jednakost (tzv. jednakost paralelograma), npr. direktnim raspisivanjem:
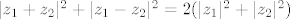
Sada iskoristimo NZPsredine uz r=2, s=n, zatim upotrijebimo gornju jednakost te konačno iskoristimo NZPsume uz r=2, s=n:
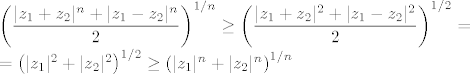
Preostaje sve dignuti na n-tu i pomnožiti s 2.
Desna nejednakost se dobije iz lijeve kako reče Martinab.
Ako nešto ipak treba detaljnije raspisati, samo pitaj. Nadam se da ovo nije neki "dječji" zadačić pa sam bezveze zakomplicirao. 
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
|








