|
[quote="Anonymous"]Imam velikih problema sa rješavanjem nelinearnih sustava koji se redovno javljaju kod računanja extrema na rubu kompakntog skupa, pa me zanima da li postoji kakva 'kuharica' za njihovo rješavanje.[/quote]
Nema kuharice... maksimalno pojednostavniti, probati smanjiti broj nepoznanica,...
[quote]Također bilo bi odlično kad bi netko mogao rješiti sljedeći sustav:
4x - y = 2Lx
4z^2 - x = 2Ly
8zy + 64 = 2Lz
x^2 + y^2 + z^2 -100 = 0
[/quote]
Vidim da je funkcija bila f(x,y)=2x^2-xy+64z+4yz^2, pa sam u papirima našla i tekst zadatka: Dokažite da funkcija [latex]f:\overline{K(0,10)}\rightarrow R[/latex] dostiže ekstreme na rubu domene.
Tu nije potrebno rješavati ovaj sustav! Naime, ne tražimo ekstreme na rubu, samo želimo dokazati da su baš tamo. Prvo potražimo ekstreme u unutrašnjosti, vidimo da ih nema, pa zaključimo (kompaktnost, nepr.fja) da se ekstremi moraju postizati na rubu.
| Anonymous (napisa): | | Imam velikih problema sa rješavanjem nelinearnih sustava koji se redovno javljaju kod računanja extrema na rubu kompakntog skupa, pa me zanima da li postoji kakva 'kuharica' za njihovo rješavanje. |
Nema kuharice... maksimalno pojednostavniti, probati smanjiti broj nepoznanica,...
| Citat: | Također bilo bi odlično kad bi netko mogao rješiti sljedeći sustav:
4x - y = 2Lx
4z^2 - x = 2Ly
8zy + 64 = 2Lz
x^2 + y^2 + z^2 -100 = 0
|
Vidim da je funkcija bila f(x,y)=2x^2-xy+64z+4yz^2, pa sam u papirima našla i tekst zadatka: Dokažite da funkcija 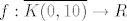 dostiže ekstreme na rubu domene. dostiže ekstreme na rubu domene.
Tu nije potrebno rješavati ovaj sustav! Naime, ne tražimo ekstreme na rubu, samo želimo dokazati da su baš tamo. Prvo potražimo ekstreme u unutrašnjosti, vidimo da ih nema, pa zaključimo (kompaktnost, nepr.fja) da se ekstremi moraju postizati na rubu.
|




