| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 12:12 sri, 25. 1. 2006 Naslov: Zadatak sa kolokvija Postano: 12:12 sri, 25. 1. 2006 Naslov: Zadatak sa kolokvija |
    |
|
|
Zadatak koji ne znam je sa 2. kolokvija 2003. godine a glasi
Zadana je funkcija F: [latex]<0,\frac{\pi}{4}>[/latex] X R -> R
[latex]F(x,y)= cos(x+2y) - \frac{x}{\sqrt{2}} - \sqrt{2}y[/latex]
Dokažite da postoji funkcija f : [latex]<0,\frac{\pi}{4}>[/latex] -> R^+(pozitivni realni), f je klase C^1 na domeni takva da je F(x,f(x))=0 za svaki x iz [latex]<0,\frac{\pi}{4}>[/latex]
Sad bih trebao prvo za svaki fiksni x_0 iz [latex]<0,\frac{\pi}{4}>[/latex] pokazati da za njega postoji jednistveni y_0 takav da je f(x_0, y_0)=0 i u svrhu toga analiziram funkciju [latex]g(y)= cos(x_0+2y) - \frac{x_0}{\sqrt{2}} - \sqrt{2}y[/latex]
Očito je [latex]lim_{y->0^+}=cosx_0 - \frac{x_0}{\sqrt{2}} > 0[/latex] i [latex]lim_{y->+besk.}=- besk. < 0[/latex] i sad mi treba da je derivacija funkcije strogo manja od nule odn. da f-ja pada da bih mogao zaključiti da postoji takav jedinstveni y_0 nultočka od g na R^+.
No kako je derivacija jednaka [latex]g'(x)=-2sin(x_0+2y)-\sqrt{2}[/latex] to očito nije slučaj, nego na većem dijelu pada, a na manjem raste(periodički). Jednadžba g(y)=0 se ne može eksplicitno riješiti, pokušao sam još na par načina analizirati funkciju ali ništa.
Ne znam kako da iz ovoga šta imam zaključim da postoji jednistvena nultočka f-je g :?
Zadatak koji ne znam je sa 2. kolokvija 2003. godine a glasi
Zadana je funkcija F: 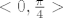 X R → R X R → R
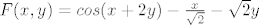
Dokažite da postoji funkcija f : 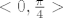 → R^+(pozitivni realni), f je klase C^1 na domeni takva da je F(x,f(x))=0 za svaki x iz → R^+(pozitivni realni), f je klase C^1 na domeni takva da je F(x,f(x))=0 za svaki x iz 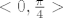
Sad bih trebao prvo za svaki fiksni x_0 iz 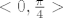 pokazati da za njega postoji jednistveni y_0 takav da je f(x_0, y_0)=0 i u svrhu toga analiziram funkciju pokazati da za njega postoji jednistveni y_0 takav da je f(x_0, y_0)=0 i u svrhu toga analiziram funkciju 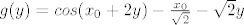
Očito je 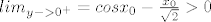 i i 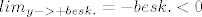 i sad mi treba da je derivacija funkcije strogo manja od nule odn. da f-ja pada da bih mogao zaključiti da postoji takav jedinstveni y_0 nultočka od g na R^+. i sad mi treba da je derivacija funkcije strogo manja od nule odn. da f-ja pada da bih mogao zaključiti da postoji takav jedinstveni y_0 nultočka od g na R^+.
No kako je derivacija jednaka 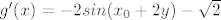 to očito nije slučaj, nego na većem dijelu pada, a na manjem raste(periodički). Jednadžba g(y)=0 se ne može eksplicitno riješiti, pokušao sam još na par načina analizirati funkciju ali ništa. to očito nije slučaj, nego na većem dijelu pada, a na manjem raste(periodički). Jednadžba g(y)=0 se ne može eksplicitno riješiti, pokušao sam još na par načina analizirati funkciju ali ništa.
Ne znam kako da iz ovoga šta imam zaključim da postoji jednistvena nultočka f-je g 
|
|
| [Vrh] |
|
Exodus
Forumaš s poteškoćama u pisanju

Pridružen/a: 18. 11. 2002. (01:38:21)
Postovi: (1C)16
Spol: 
Sarma: -
Lokacija: MA1-4
|
 Postano: 14:55 sri, 25. 1. 2006 Naslov: Re: Zadatak sa kolokvija Postano: 14:55 sri, 25. 1. 2006 Naslov: Re: Zadatak sa kolokvija |
    |
|
|
[quote="vili"]Zadatak koji ne znam je sa 2. kolokvija 2003. godine a glasi
Zadana je funkcija F: [latex]<0,\frac{\pi}{4}>[/latex] X R -> R
[latex]F(x,y)= cos(x+2y) - \frac{x}{\sqrt{2}} - \sqrt{2}y[/latex]
Dokažite da postoji funkcija f : [latex]<0,\frac{\pi}{4}>[/latex] -> R^+(pozitivni realni), f je klase C^1 na domeni takva da je F(x,f(x))=0 za svaki x iz [latex]<0,\frac{\pi}{4}>[/latex]
Sad bih trebao prvo za svaki fiksni x_0 iz [latex]<0,\frac{\pi}{4}>[/latex] pokazati da za njega postoji jednistveni y_0 takav da je f(x_0, y_0)=0 i u svrhu toga analiziram funkciju [latex]g(y)= cos(x_0+2y) - \frac{x_0}{\sqrt{2}} - \sqrt{2}y[/latex]
Očito je [latex]lim_{y->0^+}=cosx_0 - \frac{x_0}{\sqrt{2}} > 0[/latex] i [latex]lim_{y->+besk.}=- besk. < 0[/latex] i sad mi treba da je derivacija funkcije strogo manja od nule odn. da f-ja pada da bih mogao zaključiti da postoji takav jedinstveni y_0 nultočka od g na R^+.
No kako je derivacija jednaka [latex]g'(x)=-2sin(x_0+2y)-\sqrt{2}[/latex] to očito nije slučaj, nego na većem dijelu pada, a na manjem raste(periodički). Jednadžba g(y)=0 se ne može eksplicitno riješiti, pokušao sam još na par načina analizirati funkciju ali ništa.
Ne znam kako da iz ovoga šta imam zaključim da postoji jednistvena nultočka f-je g :?[/quote]
Isitna, ali nije nužno da derivacija od g bude stalnog predznaka. Naime, ako je [latex]g'(y)=-2\sin(x_0+2y)-\sqrt{2}=0[/latex]
onda je [latex]y\in S:=\{y_k:=\frac{1}{2} (\frac{3\pi}{4}+ 2k\pi -x_0): \ k \in \mathbb{Z_+\}}[/latex] (jer nas zanimaju samo pozitivni [latex]y[/latex]). No za svako [latex]y_k \in S[/latex] je [latex]g(y_k)=\cos(\frac{3\pi}{4})-\frac{1}{\sqrt{2}} \cdot x_0 - \sqrt{2}(\frac{3\pi}{8} + k\pi -\frac{x_0}{2})[/latex] [latex]=-\frac{1}{\sqrt{2}}-\sqrt{2}\cdot(\frac{3\pi}{8}+k\pi) <0 \ (k \in \mathbb{Z}_+)[/latex]. Znači, u svim točkama [latex]y_k[/latex] u kojima g ima lokalni ekstrem je [latex]g(y_k)<0[/latex], što zajedno sa onim limesima s početka daje jedinstvenu nultočku od [latex]g[/latex].
Srdačan pozdrav, vaš drug u nevolji,
dr. Exodus :croatia:
| vili (napisa): | Zadatak koji ne znam je sa 2. kolokvija 2003. godine a glasi
Zadana je funkcija F: 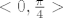 X R → R X R → R
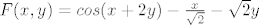
Dokažite da postoji funkcija f : 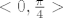 → R^+(pozitivni realni), f je klase C^1 na domeni takva da je F(x,f(x))=0 za svaki x iz → R^+(pozitivni realni), f je klase C^1 na domeni takva da je F(x,f(x))=0 za svaki x iz 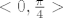
Sad bih trebao prvo za svaki fiksni x_0 iz 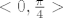 pokazati da za njega postoji jednistveni y_0 takav da je f(x_0, y_0)=0 i u svrhu toga analiziram funkciju pokazati da za njega postoji jednistveni y_0 takav da je f(x_0, y_0)=0 i u svrhu toga analiziram funkciju 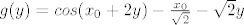
Očito je 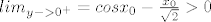 i i 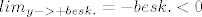 i sad mi treba da je derivacija funkcije strogo manja od nule odn. da f-ja pada da bih mogao zaključiti da postoji takav jedinstveni y_0 nultočka od g na R^+. i sad mi treba da je derivacija funkcije strogo manja od nule odn. da f-ja pada da bih mogao zaključiti da postoji takav jedinstveni y_0 nultočka od g na R^+.
No kako je derivacija jednaka 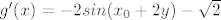 to očito nije slučaj, nego na većem dijelu pada, a na manjem raste(periodički). Jednadžba g(y)=0 se ne može eksplicitno riješiti, pokušao sam još na par načina analizirati funkciju ali ništa. to očito nije slučaj, nego na većem dijelu pada, a na manjem raste(periodički). Jednadžba g(y)=0 se ne može eksplicitno riješiti, pokušao sam još na par načina analizirati funkciju ali ništa.
Ne znam kako da iz ovoga šta imam zaključim da postoji jednistvena nultočka f-je g  |
Isitna, ali nije nužno da derivacija od g bude stalnog predznaka. Naime, ako je 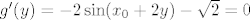
onda je 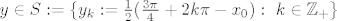 (jer nas zanimaju samo pozitivni (jer nas zanimaju samo pozitivni  ). No za svako ). No za svako  je je 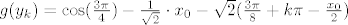 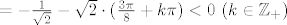 . Znači, u svim točkama . Znači, u svim točkama 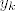 u kojima g ima lokalni ekstrem je u kojima g ima lokalni ekstrem je 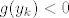 , što zajedno sa onim limesima s početka daje jedinstvenu nultočku od , što zajedno sa onim limesima s početka daje jedinstvenu nultočku od  . .
Srdačan pozdrav, vaš drug u nevolji,
dr. Exodus 
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Exodus
Forumaš s poteškoćama u pisanju

Pridružen/a: 18. 11. 2002. (01:38:21)
Postovi: (1C)16
Spol: 
Sarma: -
Lokacija: MA1-4
|
 Postano: 15:36 sri, 25. 1. 2006 Naslov: Re: Zadatak sa kolokvija Postano: 15:36 sri, 25. 1. 2006 Naslov: Re: Zadatak sa kolokvija |
    |
|
|
[quote="vili"]Cool 8)
Prvo i prvo, mucho hvala na rješenju.
[quote="Exodus"]Istina, ali nije nužno da derivacija od g bude stalnog predznaka.[/quote]
Znam, i ovako nešto sam zapravo tražio.
Samo mali ispravak: S bi trebao biti oblika
[latex]S:=\{\frac{1}{2} (\frac{5\pi}{4}+ 2k\pi -x_0): \ k \in \mathbb{Z_+\}}[/latex] U [latex]\{\frac{1}{2} (\frac{7\pi}{4}+ 2k\pi -x_0): \ k \in \mathbb{Z_+\}}[/latex]
ne?[/quote]
:shock: aha, jeste, je, imaš pravo... znači sve 3 (trice) u mom prijašnjem postu treba zamijeniti s 5 (peticama) ili 7 (sedmicama), pa će i sve dalje štimati. :lol: da.
srdačan pozdrav,
dr. Exodus :croatia:
| vili (napisa): | Cool 
Prvo i prvo, mucho hvala na rješenju.
| Exodus (napisa): | | Istina, ali nije nužno da derivacija od g bude stalnog predznaka. |
Znam, i ovako nešto sam zapravo tražio.
Samo mali ispravak: S bi trebao biti oblika
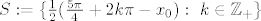 U U 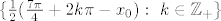
ne? |
 aha, jeste, je, imaš pravo... znači sve 3 (trice) u mom prijašnjem postu treba zamijeniti s 5 (peticama) ili 7 (sedmicama), pa će i sve dalje štimati. aha, jeste, je, imaš pravo... znači sve 3 (trice) u mom prijašnjem postu treba zamijeniti s 5 (peticama) ili 7 (sedmicama), pa će i sve dalje štimati.  da. da.
srdačan pozdrav,
dr. Exodus 
|
|
| [Vrh] |
|
|








