|
[quote="bibi"]Može li se funkcija f(x,y,z)=(xXyXz^2-x^3)\(x^2+z^2) proširiti na y-os tako da bude diferencijabilna u barem jednoj točki y-osi?[/quote]
Hmm.. evo u ove kasne sate pokušat ću vam pomoći.. ukoliko mi dozvolite. :?
Nasreću, odgovor je DA.... :D
Prvo primijetimo da je [latex]f[/latex] definirana na komplementu y-osi, gdje je i neprekidna, te se može proširiti do neprekidne funkcije na čitavi [latex]\mathbb{R}^3[/latex], i to tako da dodefiniramo [latex]f(0,y,0):=0, \ \forall y \in \mathbb{R}[/latex].
Fiksirajmo neki [latex]y_0 \in \mathbb{R}[/latex] i dokažimo da je [latex]f[/latex] zaista neprekidna u točki [latex]T_0:=(0,y_0,0)[/latex].
Neka je dan [latex]\varepsilon>0[/latex], stavimo [latex]\delta:=\min\{1,\frac{\varepsilon}{3+2|y_0|}\}[/latex] i uzmimo točku [latex] T:=(x,y,z) \in K(T_0,\delta)[/latex]. Tada je svakako [latex]|x|,|y-y_0|<\sqrt{x^2+(y-y_0)^2+z^2}<\delta \leq 1[/latex], pa imamo
[latex]|f(T)-f(T_0)|=|f(T)|=|\frac{xyz^2-x^3}{x^2+z^2}|=
|\frac{|xy(z^2-x^2)+x^3(y-1)|}{x^2+z^2} \leq[/latex] [latex]|xy|\frac{|x^2-z^2|}{x^2+z^2}+|x||y-1|\frac{x^2}{x^2+z^2}[/latex]
[latex]\leq |x||y|+|x||y-1|\leq(2|y|+1)|x|
\leq [/latex] [latex](2|y-y_0|+2|y_0|+1|)|x| < (3+2|y_0|)|x| < \varepsilon[/latex], budući je
[latex]\frac{|x^2-z^2|}{x^2+z^2}\leq \frac{x^2+z^2}{x^2+z^2}=1[/latex] i [latex]\frac{x^2}{x^2+z^2}\leq \frac{x^2+z^2}{x^2+z^2}=1[/latex].
Sada zbog proizvoljnosti točke [latex]T_0 \in K(T_0,\delta)[/latex], [latex]\varepsilon>0[/latex] i točke [latex]y_0 \in \mathbb{R}[/latex] slijedi tvrdnja.
Pogledajmo sada parcijalne derivacije od [latex]f[/latex] u točkama y-osi. Neka je, kao i prije [latex]T_0=(0,y_0,0), \ y_0 \in \mathbb{R}[/latex].
Imamo redom:
[latex]\partial_{e_1}f(T_0)=\lim_{t \rightarrow 0} \frac{ f(T_0+te_1)-f(T_0)}{t}=\lim_{t \rightarrow 0} \frac{ f(t,y_0,0)}{t}=\lim_{t \rightarrow 0} \frac{-t^3}{t^3}=-1. [/latex]
[latex]\partial_{e_2}f(T_0)=\lim_{t \rightarrow 0} \frac{ f(T_0+te_2)-f(T_0)}{t}=\lim_{t \rightarrow 0} \frac{ f(0,t+y_0,0)}{t}=\lim_{t \rightarrow 0} \frac{0}{t}=0. [/latex]
[latex]\partial_{e_3}f(T_0)=\lim_{t \rightarrow 0} \frac{ f(T_0+te_3)-f(T_0)}{t}=\lim_{t \rightarrow 0} \frac{ f(0,y_0,t)}{t}=\lim_{t \rightarrow 0} \frac{0}{t}=0. [/latex]
Dakle ukoliko diferencijal [latex]Df(T_0)[/latex] postoji, njegova matrica u kanonskoj bazi mora biti [latex][-1,0,0][/latex]. Kada bi to bila istina, onda bi moralo biti
[latex]\textbf{(*)} 0=\lim_{h=(h_1,h_2,h_3) \rightarrow 0}\frac{f(T_0+h)-f(T_0)-Df(T_0)h}{\|h\|}=\lim_{h=(h_1,h_2,h_3) \rightarrow 0}\frac{f(T_0+h)+h_1}{\|h\|}[/latex]
[latex]=\lim_{h=(h_1,h_2,h_3) \rightarrow 0}\frac{f(h_1,h_2+y_0,h_3)+h_1}{\sqrt{h_1^2+h_2^2+h_3^2}}[/latex][latex]=\lim_{h=(h_1,h_2,h_3) \rightarrow 0}\frac{h_1(h_2+y_0)h_3^2-h_1^3+h_1(h_1^2+h_3^2)}{\sqrt{h_1^2+h_2^2+h_3^2}\cdot (h_1^2+h_3^2)}=[/latex] [latex]\lim_{h=(h_1,h_2,h_3) \rightarrow 0}\frac{h_1(h_2+y_0)h_3^2+h_1h_3^2}{\sqrt{h_1^2+h_2^2+h_3^2}\cdot (h_1^2+h_3^2)}[/latex]
Označimo sa [latex]G(h_1,h_2,h_3):=\frac{h_1(h_2+y_0)h_3^2+h_1 h_3^2}{\sqrt{h_1^2+h_2^2+h_3^2}\cdot (h_1^2+h_3^2)}[/latex] i pogledajmo niz [latex](h_n)_n[/latex] zadan formulom [latex]h_n:=(\frac{1}{n},0,\frac{1}{n})[/latex]. Očito je [latex]\lim_{n \rightarrow \infty}h_n=0[/latex], no niz [latex](G(h_n))_n[/latex] će konvergirati prema [latex]0[/latex] akko je [latex]y_0=-1[/latex]. Naime, imamo
[latex]G(h_n)=\frac{\frac{1}{n^3} y_0 +\frac{1}{n^3}}{\frac{\sqrt{2}}{n} \cdot \frac{2}{n^2}}=\frac{y_0+1}{2 \sqrt{2}}[/latex], tj. niz [latex](G(h_n))_n[/latex] je stacionaran, pa će biti [latex]\lim_{n \rightarrow \infty}G(h_n)=0[/latex] jedino za [latex]y_0=0[/latex].
Znači jedini kandidat točke s y-osi u kojoj je [latex]f[/latex] eventualno diferencijabilna je točka [latex]T_0=(0,-1,0)[/latex].
Dokažimo na kraju da je proširenje od [latex]f[/latex] po neprekidnosti zaista diferencijabilno u točki [latex]T_0[/latex]. Ako uvrsimo [latex]y_0=-1[/latex] u funkciju [latex]G[/latex] dobit ćemo
[latex]G(h_1,h_2,h_3)=\frac{h_1h_2h_3^2}{\sqrt{h_1^2+h_2^2+h_3^2}\cdot (h_1^2+h_3^2)}[/latex].
Neka je ponovo dan [latex]\varepsilon >0[/latex], neka je [latex]\delta:=\varepsilon[/latex] i neka je [latex]T=(h_1,h_2,h_3)\in K(0,\delta)[/latex]. Tada je svakako [latex]|h_1|\leq \sqrt{h_1^2+h_2^2+h_3^2}< \delta=\varepsilon [/latex], pa je
[latex]|G(h_1,h_2,h_3)|=\frac{|h_1h_2h_3^2|}{\sqrt{h_1^2+h_2^2+h_3^2}\cdot (h_1^2+h_3^2)} \leq \frac{|h_1h_2h_3^2|}{\sqrt{h_1^2+h_2^2+h_3^2}\cdot h_3^2} =
|h_1|\frac{|h_2|}{\sqrt{h_1^2+h_2^2+h_3^2}}[/latex] [latex]\leq |h_1|\frac{\sqrt{h_1^2+h_2^2+h_3^2}}{\sqrt{h_1^2+h_2^2+h_3^2}}=|h_1| < \varepsilon. [/latex]
Dakle, za [latex]y_0=-1[/latex] limes u [b](*)[/b] postoji i jednak je [latex]0[/latex], tj. [latex]f[/latex] je zaista diferencijabilna u točki [latex](0,-1,0)[/latex] i to je jedina točka s y-osi u kojoj je proširenje od f po neprekidnosti diferencijabilno. Vidi vraga, ah... :drinking:
Srdačan pozdrav, vaš istinski drug i kolega,
dr. Exodus :croatia:[b][/b]
| bibi (napisa): | | Može li se funkcija f(x,y,z)=(xXyXz^2-x^3)\(x^2+z^2) proširiti na y-os tako da bude diferencijabilna u barem jednoj točki y-osi? |
Hmm.. evo u ove kasne sate pokušat ću vam pomoći.. ukoliko mi dozvolite. 
Nasreću, odgovor je DA.... 
Prvo primijetimo da je  definirana na komplementu y-osi, gdje je i neprekidna, te se može proširiti do neprekidne funkcije na čitavi definirana na komplementu y-osi, gdje je i neprekidna, te se može proširiti do neprekidne funkcije na čitavi 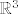 , i to tako da dodefiniramo , i to tako da dodefiniramo 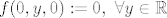 . .
Fiksirajmo neki 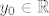 i dokažimo da je i dokažimo da je  zaista neprekidna u točki zaista neprekidna u točki 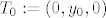 . .
Neka je dan 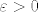 , stavimo , stavimo 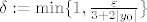 i uzmimo točku i uzmimo točku 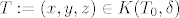 . Tada je svakako . Tada je svakako 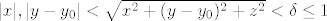 , pa imamo , pa imamo
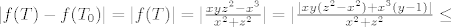 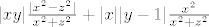
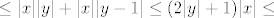 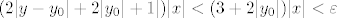 , budući je , budući je
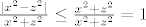 i i 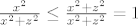 . .
Sada zbog proizvoljnosti točke 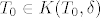 , , 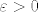 i točke i točke 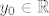 slijedi tvrdnja. slijedi tvrdnja.
Pogledajmo sada parcijalne derivacije od  u točkama y-osi. Neka je, kao i prije u točkama y-osi. Neka je, kao i prije 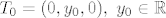 . .
Imamo redom:
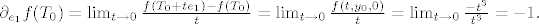
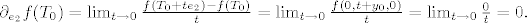
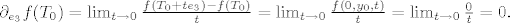
Dakle ukoliko diferencijal 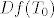 postoji, njegova matrica u kanonskoj bazi mora biti postoji, njegova matrica u kanonskoj bazi mora biti 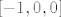 . Kada bi to bila istina, onda bi moralo biti . Kada bi to bila istina, onda bi moralo biti
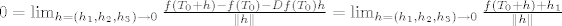
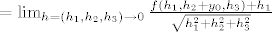 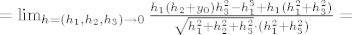 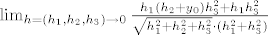
Označimo sa 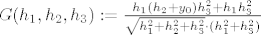 i pogledajmo niz i pogledajmo niz 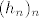 zadan formulom zadan formulom 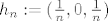 . Očito je . Očito je 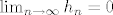 , no niz , no niz 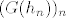 će konvergirati prema će konvergirati prema  akko je akko je 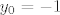 . Naime, imamo . Naime, imamo
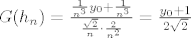 , tj. niz , tj. niz 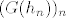 je stacionaran, pa će biti je stacionaran, pa će biti 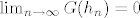 jedino za jedino za 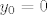 . .
Znači jedini kandidat točke s y-osi u kojoj je  eventualno diferencijabilna je točka eventualno diferencijabilna je točka 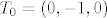 . .
Dokažimo na kraju da je proširenje od  po neprekidnosti zaista diferencijabilno u točki po neprekidnosti zaista diferencijabilno u točki 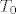 . Ako uvrsimo . Ako uvrsimo 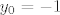 u funkciju u funkciju 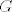 dobit ćemo dobit ćemo
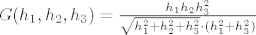 . .
Neka je ponovo dan 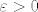 , neka je , neka je 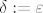 i neka je i neka je 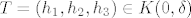 . Tada je svakako . Tada je svakako 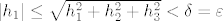 , pa je , pa je
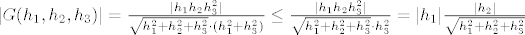 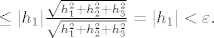
Dakle, za 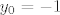 limes u (*) postoji i jednak je limes u (*) postoji i jednak je  , tj. , tj.  je zaista diferencijabilna u točki je zaista diferencijabilna u točki 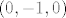 i to je jedina točka s y-osi u kojoj je proširenje od f po neprekidnosti diferencijabilno. Vidi vraga, ah... i to je jedina točka s y-osi u kojoj je proširenje od f po neprekidnosti diferencijabilno. Vidi vraga, ah... 
Srdačan pozdrav, vaš istinski drug i kolega,
dr. Exodus 
|




