| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
>Kristina>
Gost
|
 Postano: 19:54 čet, 9. 2. 2006 Naslov: x^5 + 1 = 0 Postano: 19:54 čet, 9. 2. 2006 Naslov: x^5 + 1 = 0 |
    |
|
|
Jako sam ljuta sama ne sebe i zbunjena jer ne znam rijesit taj zadatak!
Pokusala jesam, vec nekoliko dana, ali ne ide. Molim vas svih za pomoc!
Ovako - x^5 = -1
U komplexnoj ravnini..
Znam da je rjesenje toga tocke pravilnog peterokuta upisanog jedinicnoj kruznici, ali koje su?
(x1,y1) = (-1, 0)
plus jos cetiri komlpeksna broja, tj 2 konjugirana.. Ali njih ne znam dobit. I znam da su u trigonometrijskom obliku..
Molim Vas za jedan kraci postupak samo da se prisjetim toga..
Jako sam ljuta sama ne sebe i zbunjena jer ne znam rijesit taj zadatak!
Pokusala jesam, vec nekoliko dana, ali ne ide. Molim vas svih za pomoc!
Ovako - x^5 = -1
U komplexnoj ravnini..
Znam da je rjesenje toga tocke pravilnog peterokuta upisanog jedinicnoj kruznici, ali koje su?
(x1,y1) = (-1, 0)
plus jos cetiri komlpeksna broja, tj 2 konjugirana.. Ali njih ne znam dobit. I znam da su u trigonometrijskom obliku..
Molim Vas za jedan kraci postupak samo da se prisjetim toga..
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 20:07 čet, 9. 2. 2006 Naslov: Postano: 20:07 čet, 9. 2. 2006 Naslov: |
    |
|
|
Nacrtaj si trigonometrijsku kruznicu, i spomenuti peterokut. :)
Rijec je o tockama s medjusobnim otklonom od [latex]\frac{2 \pi}{5}[/latex] (ili [latex]\frac{360^\circ}{5} = 72^\circ[/latex], ako ti je tako draze). 8)
Onda uvrstis te kuteve u trigonometrijske jednadzbe i dobijes da su ti rjesenja:
[latex]x_k = \cos (\pi + \frac{2k \pi}{5}) + i \sin (\pi + \frac{2k \pi}{5}), k \in \{0,1,2,3,4\}[/latex]
Malo sredis i imas:
[latex]x_k = -\cos \frac{2k \pi}{5} - i \sin \frac{2k \pi}{5}, k \in \{0,1,2,3,4\}[/latex]
(A moglo se i bez sredjivanja - samo primijetis da je slika simetricna u odnosu na x^5=1, pa mnozis ta rjesenja s -1 8))
:wave:
Nacrtaj si trigonometrijsku kruznicu, i spomenuti peterokut. 
Rijec je o tockama s medjusobnim otklonom od 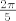 (ili (ili 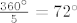 , ako ti je tako draze). , ako ti je tako draze). 
Onda uvrstis te kuteve u trigonometrijske jednadzbe i dobijes da su ti rjesenja:
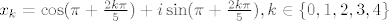
Malo sredis i imas:
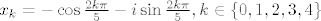
(A moglo se i bez sredjivanja - samo primijetis da je slika simetricna u odnosu na x^5=1, pa mnozis ta rjesenja s -1  ) )

_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 20:15 čet, 9. 2. 2006 Naslov: Postano: 20:15 čet, 9. 2. 2006 Naslov: |
    |
|
|
Dakle, znas da su te tocke tocke pravilnog peterokuta upisanog jedinicnoj kruznici. Sredisnji kut nad svakom od stranica tog peterokuta je [latex]\frac{2\pi}{5}[/latex]
S druge strane, koordinate tocke na jedinicnoj kruznici su [latex](\cos \phi, \sin \phi)[/latex], gdje je [latex]\phi[/latex] kut koji polupravac iz ishodista kroz tu tocku zatvara sa pozitivnim dijelom x - osi (malo nespretno i nepotpuno objasnjeno ali znas na sto mislim valjda :P). Kako za izracunatu tocku vec imas [latex]\phi = \pi[/latex], rjesenja gornje jednadzbe su oblika:
[latex]\cos (\pi + k\frac{2\pi}{5}) + i \sin (\pi + k\frac{2\pi}{5}), k = -2, -1, 0, 1, 2[/latex]
edit - loshe, loshe, prestignut sam, i jos je ljepshe nego moje :tso:
Dakle, znas da su te tocke tocke pravilnog peterokuta upisanog jedinicnoj kruznici. Sredisnji kut nad svakom od stranica tog peterokuta je 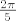
S druge strane, koordinate tocke na jedinicnoj kruznici su 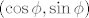 , gdje je , gdje je 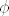 kut koji polupravac iz ishodista kroz tu tocku zatvara sa pozitivnim dijelom x - osi (malo nespretno i nepotpuno objasnjeno ali znas na sto mislim valjda kut koji polupravac iz ishodista kroz tu tocku zatvara sa pozitivnim dijelom x - osi (malo nespretno i nepotpuno objasnjeno ali znas na sto mislim valjda  ). Kako za izracunatu tocku vec imas ). Kako za izracunatu tocku vec imas 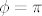 , rjesenja gornje jednadzbe su oblika: , rjesenja gornje jednadzbe su oblika:
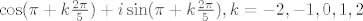
edit - loshe, loshe, prestignut sam, i jos je ljepshe nego moje 
_________________
Bri
|
|
| [Vrh] |
|
>Kristina>
Gost
|
 Postano: 21:22 čet, 9. 2. 2006 Naslov: Postano: 21:22 čet, 9. 2. 2006 Naslov: |
    |
|
|
Decki zlatni ste!
Hvala hvala hvala....
Malo me zbunjivalo to sto u trigonometrijskim formulama pise
cos[(fi + 2*k*pi)/n], k=0,1,...,n-1
i cijelo vrijeme sam se borila s tim fi, sto on predstavlja u cijeloj prici. Zaboravila sam..
Hvala jos jednom! :D
Decki zlatni ste!
Hvala hvala hvala....
Malo me zbunjivalo to sto u trigonometrijskim formulama pise
cos[(fi + 2*k*pi)/n], k=0,1,...,n-1
i cijelo vrijeme sam se borila s tim fi, sto on predstavlja u cijeloj prici. Zaboravila sam..
Hvala jos jednom! 
|
|
| [Vrh] |
|
|






