|
[quote="Anonymous"]Moze li neko pojasniti razliku izmedju pogreske interpolacije i ocjene pogreske. Jer bas ne razumijem ove pojmove:
Prava pogreska interpolacije
Ocjena lokalne pogreske
Pogreška interpolaijena cijelom intervalu
Ocjena pogreske na cijelom int.[/quote]
Npr. uzmimo da neprekidnu funkciju [latex]f[/latex] na segmentu [latex][a,b][/latex] interpoliramo polinomom [latex]p_n[/latex] stupnja [latex]n[/latex] na mreži [latex]a= x_0 < x_1 < \cdots < x_n = b[/latex]. Tada je
- [b]Prava pogreška interpolacje u točki[/b] [latex]c \in [a,b][/latex] je naprosto [latex]|f(c)-p_n(c)|[/latex].
- Ako je [latex]f[/latex] klase [latex]C^{n+1}([a,b])[/latex] tada imamo [b]ocjenu pogreške interpolacije u točki[/b] [latex]c \in [a,b][/latex]: [latex] |f(c)-p_n(c)|\leq \frac{|\prod_{i=0}^{n}(c-x_i)|}{(n+1)!}M_{n+1}f[/latex], gdje je [latex]M_{n+1}f=\max\{|f^{(n+1)}(x)|: \ x \in [a,b]\} [/latex].
- [b]Uniformna[/b] (makismalna, ili pogreška interpolacije na cijelom segmentu [latex][a,b][/latex] je) [latex]\|f-p_n\|_{\infty}^{[a,b]}=\max\{|f(x)-p_n(x)|: \ x \in [a,b]\}[/latex].
- Ako je [latex]f[/latex] ponovo klase [latex]C^{n+1}([a,b])[/latex], tada imamo [b]ocjenu uniformne pogreške [/b][latex]\|f-p_n\|_{\infty}^{[a,b]}\leq \frac{\omega(x_0,\cdots ,x_n)}{(n+1)!}M_{n+1}f[/latex], gdje je [latex]\omega(x_0,\ldots ,x_n):=\max \{|\prod_{i=0}^{n}(x-x_i)|: \ x \in [a,b]\}[/latex]
| Anonymous (napisa): | Moze li neko pojasniti razliku izmedju pogreske interpolacije i ocjene pogreske. Jer bas ne razumijem ove pojmove:
Prava pogreska interpolacije
Ocjena lokalne pogreske
Pogreška interpolaijena cijelom intervalu
Ocjena pogreske na cijelom int. |
Npr. uzmimo da neprekidnu funkciju  na segmentu na segmentu 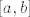 interpoliramo polinomom interpoliramo polinomom 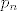 stupnja stupnja  na mreži na mreži 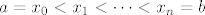 . Tada je . Tada je
- Prava pogreška interpolacje u točki 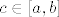 je naprosto je naprosto 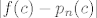 . .
- Ako je  klase klase 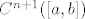 tada imamo ocjenu pogreške interpolacije u točki tada imamo ocjenu pogreške interpolacije u točki 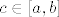 : : 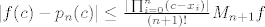 , gdje je , gdje je 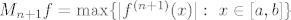 . .
- Uniformna (makismalna, ili pogreška interpolacije na cijelom segmentu 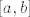 je) je) 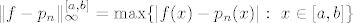 . .
- Ako je  ponovo klase ponovo klase 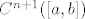 , tada imamo ocjenu uniformne pogreške , tada imamo ocjenu uniformne pogreške 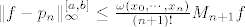 , gdje je , gdje je 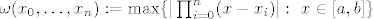
|




