Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

jedinstvenost funkcije
WWW:

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
nana
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: žensko
Sarma = la pohva - posuda
95 = 158 - 63
PostPostano: 13:04 sri, 15. 2. 2006    Naslov: jedinstvenost funkcije Citirajte i odgovorite
Zanima me kako pokazati da je fja e^x : Z --> R jedinstvena.
tj. nemam ideju kako bi za bilo koju fju pokazala jedinstvenost (osim mozda za determinantnu :D )

Hvala
Zanima me kako pokazati da je fja e^x : Z --> R jedinstvena.
tj. nemam ideju kako bi za bilo koju fju pokazala jedinstvenost (osim mozda za determinantnu Very Happy )

Hvala



_________________
Kad sam bila mala htjela sam biti statističarka Very Happy
[tex]\omega \in \Omega[/tex] Srce
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
nana
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: žensko
Sarma = la pohva - posuda
95 = 158 - 63
PostPostano: 14:29 sri, 15. 2. 2006    Naslov: Citirajte i odgovorite
jos jedno pitanjce.
Zasto nam je vazno pokazati da je sin neprekidan u 0? tj. zasto bas u 0
jos jedno pitanjce.
Zasto nam je vazno pokazati da je sin neprekidan u 0? tj. zasto bas u 0



_________________
Kad sam bila mala htjela sam biti statističarka Very Happy
[tex]\omega \in \Omega[/tex] Srce
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
goranm
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
218 = 249 - 31
PostPostano: 17:19 sri, 15. 2. 2006    Naslov: Citirajte i odgovorite
[quote="nana"]jos jedno pitanjce.
Zasto nam je vazno pokazati da je sin neprekidan u 0? tj. zasto bas u 0[/quote]
možda zbog:
[latex]\lim_{x \to 0} {\frac{sin{x}}{x}}=1[/latex] ? :-k
nana (napisa):
jos jedno pitanjce.
Zasto nam je vazno pokazati da je sin neprekidan u 0? tj. zasto bas u 0

možda zbog:
? Think



_________________
The Dude Abides
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
rose
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 16. 12. 2005. (22:16:57)
Postovi: (7)16
Sarma = la pohva - posuda
8 = 8 - 0
PostPostano: 17:20 sri, 15. 2. 2006    Naslov: Re: jedinstvenost funkcije Citirajte i odgovorite
[quote="nana"]Zanima me kako pokazati da je fja e^x : Z --> R jedinstvena.
[/quote]

Zadana je funkcija g sa svojstvima:
g(m+n)=g(m)g(n)
g(1)=e

g(2)=g(1+1)=g(1)g(1)=e^2
dalje induktivno pokazujemo za prirodne brojeve:
ako je g(n)=e^n onda je g(n+1)=g(n)g(1)=e^n*e=e^n+1
e=g(1)=g(0+1)=g(0)g(1)=g(0)*e => g(0)=1
1=g(0)=g(n+(-n))=g(n)g(-n) => g(-n)=1/g(n)=1/e^n


[quote="nana"]
Zasto nam je vazno pokazati da je sin neprekidan u 0? tj. zasto bas u 0
[/quote]

Kad pokazemo da je sin i cos neprekinut u 0, onda mozemo pokazati da je funkcija sin neprekidna u svakoj tocki.
nana (napisa):
Zanima me kako pokazati da je fja e^x : Z –> R jedinstvena.


Zadana je funkcija g sa svojstvima:
g(m+n)=g(m)g(n)
g(1)=e

g(2)=g(1+1)=g(1)g(1)=e^2
dalje induktivno pokazujemo za prirodne brojeve:
ako je g(n)=e^n onda je g(n+1)=g(n)g(1)=e^n*e=e^n+1
e=g(1)=g(0+1)=g(0)g(1)=g(0)*e => g(0)=1
1=g(0)=g(n+(-n))=g(n)g(-n) => g(-n)=1/g(n)=1/e^n


nana (napisa):

Zasto nam je vazno pokazati da je sin neprekidan u 0? tj. zasto bas u 0


Kad pokazemo da je sin i cos neprekinut u 0, onda mozemo pokazati da je funkcija sin neprekidna u svakoj tocki.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Martinab
Moderator
Moderator


Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
Sarma = la pohva - posuda
143 = 167 - 24
PostPostano: 21:42 sri, 15. 2. 2006    Naslov: Citirajte i odgovorite
Rose, mislim da ti fali dio dokaza. Nakon sto dokazes da je g(x)=e^x za sve cijele brojeve, slicno se pokaze da isto vrijedi za sve racionalne brojeve. Nakon toga koristis cinjenicu koju nisi navela, a to je da je funkcija g neprekidna, pa, ako je definirana na Q (i kao takva neprekidna), onda postoji jedinstveno neprekidno prosirenje na R...
Rose, mislim da ti fali dio dokaza. Nakon sto dokazes da je g(x)=e^x za sve cijele brojeve, slicno se pokaze da isto vrijedi za sve racionalne brojeve. Nakon toga koristis cinjenicu koju nisi navela, a to je da je funkcija g neprekidna, pa, ako je definirana na Q (i kao takva neprekidna), onda postoji jedinstveno neprekidno prosirenje na R...



_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
goranm
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
218 = 249 - 31
PostPostano: 3:13 čet, 16. 2. 2006    Naslov: Citirajte i odgovorite
[quote="Martinab"]Rose, mislim da ti fali dio dokaza. Nakon sto dokazes da je g(x)=e^x za sve cijele brojeve, slicno se pokaze da isto vrijedi za sve racionalne brojeve. Nakon toga koristis cinjenicu koju nisi navela, a to je da je funkcija g neprekidna, pa, ako je definirana na Q (i kao takva neprekidna), onda postoji jedinstveno neprekidno prosirenje na R...[/quote]
Da, ali nana je tražila dokaz jedinstvenosti funkcije [latex]e^x \colon \mathbb{Z} \to \mathbb{R}[/latex], a ne [latex]e^x \colon \mathbb{R} \to \mathbb{R}[/latex] :)
Martinab (napisa):
Rose, mislim da ti fali dio dokaza. Nakon sto dokazes da je g(x)=e^x za sve cijele brojeve, slicno se pokaze da isto vrijedi za sve racionalne brojeve. Nakon toga koristis cinjenicu koju nisi navela, a to je da je funkcija g neprekidna, pa, ako je definirana na Q (i kao takva neprekidna), onda postoji jedinstveno neprekidno prosirenje na R...

Da, ali nana je tražila dokaz jedinstvenosti funkcije , a ne Smi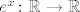le



_________________
The Dude Abides
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
nana
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: žensko
Sarma = la pohva - posuda
95 = 158 - 63
PostPostano: 8:37 čet, 16. 2. 2006    Naslov: Citirajte i odgovorite
e da je vjeko tu on bi odgovorio :cry:

hvala na pokusajima 8)
e da je vjeko tu on bi odgovorio Crying or Very sad

hvala na pokusajima Cool



_________________
Kad sam bila mala htjela sam biti statističarka Very Happy
[tex]\omega \in \Omega[/tex] Srce
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 9:24 čet, 16. 2. 2006    Naslov: Citirajte i odgovorite
[quote="nana"]e da je vjeko tu on bi odgovorio :cry:[/quote]

1. Vjeko nije mrtav; samo ga vise nema na Forumu. 8) Dakle, mozes mu se direktno javiti, ne? ;)

2. Sto od tvojih pitanja na ovom topicu nije odgovoreno? :-k
nana (napisa):
e da je vjeko tu on bi odgovorio Crying or Very sad


1. Vjeko nije mrtav; samo ga vise nema na Forumu. Cool Dakle, mozes mu se direktno javiti, ne? Wink

2. Sto od tvojih pitanja na ovom topicu nije odgovoreno? Think



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Martinab
Moderator
Moderator


Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
Sarma = la pohva - posuda
143 = 167 - 24
PostPostano: 9:39 čet, 16. 2. 2006    Naslov: Citirajte i odgovorite
:oops: vsego, mozes meni malo modificirat postavke? Tak da kad stisnem reply, dobijem pitanje "JESI LI SIGURNA DA SI PROCITALA CIJELI POST? YES NO " .... Sori na expu.

[quote]
Zasto nam je vazno pokazati da je sin neprekidan u 0? tj. zasto bas u 0
[/quote]

Pa, valjda zato jer iz cinjenice da je nepr. u 0 slijedi da je nepr. svuda. Naime, ako je sin nepr. u 0, onda je lim_{h->0} sin h=sin 0 =0 . Iz toga brzo slijedi da je i cos nepr u 0, tj. da je lim_{h->0} cos h=cos 0 =1. Ako sad pokazujes neprekidnost sinusa u bilo kojoj tocki x, onda koristeci adicijske forumle imas
lim_{h->0} sin (x+h)=lim_{h->0} (sinx cosh + cosx sinh) =sinx *1 + cos x * 0= sinx.
Embarassed vsego, mozes meni malo modificirat postavke? Tak da kad stisnem reply, dobijem pitanje "JESI LI SIGURNA DA SI PROCITALA CIJELI POST? YES NO " .... Sori na expu.

Citat:

Zasto nam je vazno pokazati da je sin neprekidan u 0? tj. zasto bas u 0


Pa, valjda zato jer iz cinjenice da je nepr. u 0 slijedi da je nepr. svuda. Naime, ako je sin nepr. u 0, onda je lim_{h->0} sin h=sin 0 =0 . Iz toga brzo slijedi da je i cos nepr u 0, tj. da je lim_{h->0} cos h=cos 0 =1. Ako sad pokazujes neprekidnost sinusa u bilo kojoj tocki x, onda koristeci adicijske forumle imas
lim_{h->0} sin (x+h)=lim_{h->0} (sinx cosh + cosx sinh) =sinx *1 + cos x * 0= sinx.



_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 9:52 čet, 16. 2. 2006    Naslov: Citirajte i odgovorite
[quote="Martinab"]:oops: vsego, mozes meni malo modificirat postavke? Tak da kad stisnem reply, dobijem pitanje "JESI LI SIGURNA DA SI PROCITALA CIJELI POST? YES NO " ....[/quote]

Ok. :twisted: Javi kad ti dosadi... ;)
Martinab (napisa):
Embarassed vsego, mozes meni malo modificirat postavke? Tak da kad stisnem reply, dobijem pitanje "JESI LI SIGURNA DA SI PROCITALA CIJELI POST? YES NO " ....


Ok. Twisted Evil Javi kad ti dosadi... Wink



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
nana
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: žensko
Sarma = la pohva - posuda
95 = 158 - 63
PostPostano: 19:35 čet, 16. 2. 2006    Naslov: Citirajte i odgovorite
[quote="vsego"]1. Vjeko nije mrtav; samo ga vise nema na Forumu. 8) Dakle, mozes mu se direktno javiti, ne? ;)

2. Sto od tvojih pitanja na ovom topicu nije odgovoreno? :-k[/quote]

1. Naravno da nije, samo sam primijetila da otkako ga nema na forumu mogu se vidjeti ugl pokusaji odgovora; prije bi on uvijek detaljno odgovorio :D

2. dokaz koji je rose ( :) ) napisala imam sa predavanja i pise za dz pokazati jedinstvenost; pa je moja pretpostavka da to sta je ona napisala nije ono sta se ocekuje

ionako mi vise ne treba :bananacaga:
svejedno puno hvala svima
vsego (napisa):
1. Vjeko nije mrtav; samo ga vise nema na Forumu. Cool Dakle, mozes mu se direktno javiti, ne? Wink

2. Sto od tvojih pitanja na ovom topicu nije odgovoreno? Think


1. Naravno da nije, samo sam primijetila da otkako ga nema na forumu mogu se vidjeti ugl pokusaji odgovora; prije bi on uvijek detaljno odgovorio Very Happy

2. dokaz koji je rose ( Smile ) napisala imam sa predavanja i pise za dz pokazati jedinstvenost; pa je moja pretpostavka da to sta je ona napisala nije ono sta se ocekuje

ionako mi vise ne treba Banana chaga (za neupucene: plese)
svejedno puno hvala svima



_________________
Kad sam bila mala htjela sam biti statističarka Very Happy
[tex]\omega \in \Omega[/tex] Srce
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2 Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan