|
Trazeni pravac mora lezati u ravnini koja sadrzi tocku i prvi pravac (jer prolazi kroz tocku i sijece pravac), a isto tako treba lezati u ravnini odredenoj tockom i drugim pravcem. Odnosno, mora lezati u presjeku tih dviju ravnina.
Za prvu ravninu uzmemo dvije tocke sa prvog pravca:
[latex]T_1 = (4, -3, 1) \\
T_2 = (1, -1, -1)[/latex]
Pa je jednadzba ravnine
[latex]\left| \begin{array}{c c c} x-1 & y+1 & z+1 \\
4 - 1 & -3 +1 & 1 + 1 \\
1 -1 & 2 + 1 & 4 + 1 \end{array} \right| = 0[/latex]
Isto to napravis i za drugi pravac i zadanu tocku, pa dobijes sustav od dvije jednadzbe i to je trazeni pravac.
Eventualno se moglo dogoditi da ti jednadzbe nisu linearno nezavisne, sto znaci da su pocetni pravci bili paralelni (sto ocito nisu zbog vektora smjera), pa bi za rjesenje dobio ravninu, a trazeni pravac bi dobio tako da uzmes pravac koji prolazi kroz zadanu tocku i proizvoljnu tocku na bilo kojem od pravaca.
Da je tocka bila na jednom od pravaca, onda bi za jednu od ravnina dobio pravac, pa bi presjek bila upravo ta tocka, ali taj je slucaj trivijalan, jer je dobar bilo koji pravac kroz tu tocku i onaj drugi pravac.
Trazeni pravac mora lezati u ravnini koja sadrzi tocku i prvi pravac (jer prolazi kroz tocku i sijece pravac), a isto tako treba lezati u ravnini odredenoj tockom i drugim pravcem. Odnosno, mora lezati u presjeku tih dviju ravnina.
Za prvu ravninu uzmemo dvije tocke sa prvog pravca:
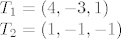
Pa je jednadzba ravnine
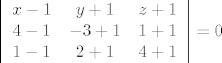
Isto to napravis i za drugi pravac i zadanu tocku, pa dobijes sustav od dvije jednadzbe i to je trazeni pravac.
Eventualno se moglo dogoditi da ti jednadzbe nisu linearno nezavisne, sto znaci da su pocetni pravci bili paralelni (sto ocito nisu zbog vektora smjera), pa bi za rjesenje dobio ravninu, a trazeni pravac bi dobio tako da uzmes pravac koji prolazi kroz zadanu tocku i proizvoljnu tocku na bilo kojem od pravaca.
Da je tocka bila na jednom od pravaca, onda bi za jednu od ravnina dobio pravac, pa bi presjek bila upravo ta tocka, ali taj je slucaj trivijalan, jer je dobar bilo koji pravac kroz tu tocku i onaj drugi pravac.
_________________
Bri
|





