| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
 Postano: 17:57 ned, 26. 2. 2006 Naslov: zbroj realnih brojeva Postano: 17:57 ned, 26. 2. 2006 Naslov: zbroj realnih brojeva |
    |
|
|
Nisam znao gdje da ovo [i]post[/i]-am, pa sam, eto, napisao tu.
Zanima me sta je zbroj svih realnih brojeva u zatvorenom intervalu od 0 do 1?
Nisam znao gdje da ovo post-am, pa sam, eto, napisao tu.
Zanima me sta je zbroj svih realnih brojeva u zatvorenom intervalu od 0 do 1?
_________________
Eat a lot, sleep a lot, brush 'em like crazy.
Run a lot, do a lot, never be lazy.
|
|
| [Vrh] |
|
Pericius2
Gost
|
 Postano: 22:50 ned, 26. 2. 2006 Naslov: Postano: 22:50 ned, 26. 2. 2006 Naslov: |
    |
|
|
Taj zbroj je [latex]+\infty[/latex]. Nadam se da možeš prihvatiti ovaj argument:
[latex]\sum_{x\in[0,1]}x\geq\sum_{x\in\{\frac{1}{n}:n\in\mathbb{N}\}}x=\sum_{n\in\mathbb{N}}\frac{1}{n}=+\infty[/latex]
(jer harmonijski red divergira)
Preciznije, takav zbroj interpretiramo ovako:
[latex]\sum_{x\in[0,1]}x=\int_{[0,1]}x\,d\mu(x)=+\infty[/latex]
(naprimjer po Leb. tm o monotonoj konv.)
Pritom je [latex]\mu[/latex]=brojeća mjera na [latex]\mathbb{R}[/latex], tj. [latex]\mu(A)=\left\{\begin{array}{ll}\mathrm{card}(A); & \textrm{za $A$ kona\v{c}an}\\+\infty; & \textrm{za $A$ beskona\v{c}an}\end{array}\right.[/latex]
Neke druge interpretacije tog "zbroja" i nisu previše smislene. (Hoću reći, mogli bismo raspravljati [i]kakva je to beskonačnost[/i] i sl.)
_______________________
"[b][i][color=darkred]Math is to sex what physics is to physics.[/color][/i][/b]"
Taj zbroj je  . Nadam se da možeš prihvatiti ovaj argument: . Nadam se da možeš prihvatiti ovaj argument:
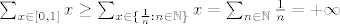
(jer harmonijski red divergira)
Preciznije, takav zbroj interpretiramo ovako:
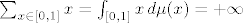
(naprimjer po Leb. tm o monotonoj konv.)
Pritom je 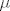 =brojeća mjera na =brojeća mjera na  , tj. , tj. 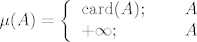
Neke druge interpretacije tog "zbroja" i nisu previše smislene. (Hoću reći, mogli bismo raspravljati kakva je to beskonačnost i sl.)
_______________________
"Math is to sex what physics is to physics."
|
|
| [Vrh] |
|
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
|
| [Vrh] |
|
Perecius3
Gost
|
|
| [Vrh] |
|
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
|
| [Vrh] |
|
Pericius4
Gost
|
|
| [Vrh] |
|
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
|
| [Vrh] |
|
Johnny Casino
Forumaš(ica)


Pridružen/a: 11. 05. 2003. (17:56:59)
Postovi: (10F)16
Spol: 
Lokacija: location, location!
|
 Postano: 14:33 uto, 28. 2. 2006 Naslov: Postano: 14:33 uto, 28. 2. 2006 Naslov: |
    |
|
|
Buduci da je na autorovo pitanje vec odgovoreno, a ne znam koliko smisla ima otvarati novi topic, napisat cu pitanje ovdje.
Bio bi jako zahvalan kad bi netko dokazao da je npr. sin neprekidna funkcija. Imam to u bilj, ali nikako ne uspijevam shvatiti...:nuts2:
Hvala!
Buduci da je na autorovo pitanje vec odgovoreno, a ne znam koliko smisla ima otvarati novi topic, napisat cu pitanje ovdje.
Bio bi jako zahvalan kad bi netko dokazao da je npr. sin neprekidna funkcija. Imam to u bilj, ali nikako ne uspijevam shvatiti...
Hvala!
_________________
Ima jedan broj, a djeljiv je sa pet
U nizu brojeva, djeljivih sa šest.
...
A to je dva, dva, dva do Žitnjaka
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 14:52 uto, 28. 2. 2006 Naslov: Postano: 14:52 uto, 28. 2. 2006 Naslov: |
    |
|
|
[quote="Johnny Casino"]Buduci da je na autorovo pitanje vec odgovoreno, a ne znam koliko smisla ima otvarati novi topic, napisat cu pitanje ovdje.
Bio bi jako zahvalan kad bi netko dokazao da je npr. sin neprekidna funkcija. Imam to u bilj, ali nikako ne uspijevam shvatiti...:nuts2:
Hvala![/quote]
Evo ti je igra sa epsilon,delta; znači neprekidnost u tocki c
|f(x) - f(c) | = |sin x - sin c | = (sinus je neparna f-ija tj. sin(-x) = - sin(x)) = |sin x + sin (-c) | = ( sin x ≤ x , za svaki x ) ≤ |x + (- c) |= |x - c | :lol: Uzmeš delta : = epsilon ,i gotov si (samo trebaš raspisati,što se meni neda, nažalost ne znam pisati u LaTex-u). Ne znam da li ste tako radili, u svakom slućaju ,javi u koliko sam nešta zabrljao :oops: .
Pozdrav
| Johnny Casino (napisa): | Buduci da je na autorovo pitanje vec odgovoreno, a ne znam koliko smisla ima otvarati novi topic, napisat cu pitanje ovdje.
Bio bi jako zahvalan kad bi netko dokazao da je npr. sin neprekidna funkcija. Imam to u bilj, ali nikako ne uspijevam shvatiti...
Hvala! |
Evo ti je igra sa epsilon,delta; znači neprekidnost u tocki c
|f(x) - f(c) | = |sin x - sin c | = (sinus je neparna f-ija tj. sin(-x) = - sin(x)) = |sin x + sin (-c) | = ( sin x ≤ x , za svaki x ) ≤ |x + (- c) |= |x - c |  Uzmeš delta : = epsilon ,i gotov si (samo trebaš raspisati,što se meni neda, nažalost ne znam pisati u LaTex-u). Ne znam da li ste tako radili, u svakom slućaju ,javi u koliko sam nešta zabrljao Uzmeš delta : = epsilon ,i gotov si (samo trebaš raspisati,što se meni neda, nažalost ne znam pisati u LaTex-u). Ne znam da li ste tako radili, u svakom slućaju ,javi u koliko sam nešta zabrljao  . .
Pozdrav
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Johnny Casino
Forumaš(ica)


Pridružen/a: 11. 05. 2003. (17:56:59)
Postovi: (10F)16
Spol: 
Lokacija: location, location!
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
|












