|
Kakav odgovor očekuješ na pitanje "koji je smisao takvih i takvih jednadžbi"? Mislim, NHF, ali ozbiljno ne znam šta bih ti rekao. :? Jel ti jasan, recimo, smisao separabilnih?
Što se tiče veze sa tm-om o impl f-ji:
Na početku imaš oblik [latex]u'=-\frac{F_1}{F_2}[/latex]
I provjeravaš dal postoji f-ja G takva da je grad G=(F_1,F_2). Prvo, onaj teorem kojim to provjeravaš se bazira na Schwarzovu tm-u.
Drugo, ako postoji takva f-ja, onda je F_1(x,u)=d_x G(x,u) i F_2(x,u)=d_u G(x,u) a početna jednadžba je dobivena iz uvjeta G(x,u)=0 iz čega vidimo da je f-ja u(x) implicitno zadana f-jom G. i na kraju, kad pogledaš kojeg je oblika parcijalna derivacija (u ovom slučaju derivacija) f-je u(x) u teoremu o implicitnoj funkciji, vidiš da je to baš naša početna (egzaktna) jednadžba.
Malo obrnut poredak svega, al anologija je tu.
Happy? :D
Kakav odgovor očekuješ na pitanje "koji je smisao takvih i takvih jednadžbi"? Mislim, NHF, ali ozbiljno ne znam šta bih ti rekao.  Jel ti jasan, recimo, smisao separabilnih?
Što se tiče veze sa tm-om o impl f-ji:
Na početku imaš oblik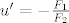 
I provjeravaš dal postoji f-ja G takva da je grad G=(F_1,F_2). Prvo, onaj teorem kojim to provjeravaš se bazira na Schwarzovu tm-u.
Drugo, ako postoji takva f-ja, onda je F_1(x,u)=d_x G(x,u) i F_2(x,u)=d_u G(x,u) a početna jednadžba je dobivena iz uvjeta G(x,u)=0 iz čega vidimo da je f-ja u(x) implicitno zadana f-jom G. i na kraju, kad pogledaš kojeg je oblika parcijalna derivacija (u ovom slučaju derivacija) f-je u(x) u teoremu o implicitnoj funkciji, vidiš da je to baš naša početna (egzaktna) jednadžba.
Malo obrnut poredak svega, al anologija je tu.
Happy? 
|
