|
[quote="Anonymous"]x^y=y^x je funkcija.kako se traži y derivirano?[/quote]
Jednakost [latex]x^y=y^x[/latex] možemo zapisati [latex]e^{y\ln x}=e^{x\ln y}[/latex] pa se sad to derivira po x:
[latex]e^{y\ln x}\cdot(y\ln x)'=e^{x\ln y}\cdot(x\ln y)'[/latex]
tj.
[latex]e^{y\ln x}\cdot(y'\ln x+y\cdot\frac{1}{x})=e^{x\ln y}\cdot(\ln y+x\cdot\frac{1}{y}\cdot y')[/latex]
tj.
[latex]x^y\cdot(y'\ln x+y\cdot\frac{1}{x})=y^x\cdot(\ln y+x\cdot\frac{1}{y}\cdot y')[/latex]
pa je konačno
[latex]y'=\displaystyle\frac{y^x\ln y-x^{y-1}y}{x^y\ln x-y^{x-1}x}[/latex]
[quote="Anonymous"]I može li diferencijalna jednadžba bit oblika npr.y''(1-x^2)=y(x^2+4x+3) ili baš mora sadržavat i y' tj. možemo ili umjesto y' pisati izraz koji smo dobili prvom derivacijom kako bi pojednostavnili izraz??Hvala[/quote]
Diferencijalna jednadžba po definiciji može sadržavati i derivacije višeg reda: y'', y''',...
Ali kod implicitnog deriviranja je [u]uvijek[/u] moguće izraziti y' pomoću x i y.
Naprosto, ako jednadžba glasi F(x,y)=0, onda je
[latex]y'=-\displaystyle\frac{\frac{\partial}{\partial x}F(x,y)}{\frac{\partial}{\partial y}F(x,y)}[/latex]
ali se na Analizi 2 još ne spominju parcijalne derivacije.
| Anonymous (napisa): | | x^y=y^x je funkcija.kako se traži y derivirano? |
Jednakost 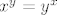 možemo zapisati možemo zapisati  pa se sad to derivira po x: pa se sad to derivira po x:

tj.
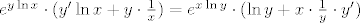
tj.
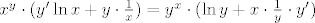
pa je konačno
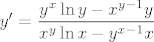
| Anonymous (napisa): | | I može li diferencijalna jednadžba bit oblika npr.y''(1-x^2)=y(x^2+4x+3) ili baš mora sadržavat i y' tj. možemo ili umjesto y' pisati izraz koji smo dobili prvom derivacijom kako bi pojednostavnili izraz??Hvala |
Diferencijalna jednadžba po definiciji može sadržavati i derivacije višeg reda: y'', y''',...
Ali kod implicitnog deriviranja je uvijek moguće izraziti y' pomoću x i y.
Naprosto, ako jednadžba glasi F(x,y)=0, onda je
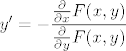
ali se na Analizi 2 još ne spominju parcijalne derivacije.
|




