| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
 Postano: 9:39 sub, 22. 4. 2006 Naslov: Postano: 9:39 sub, 22. 4. 2006 Naslov: |
    |
|
|
Nisu vas zalockali!?
Hmm, izgleda da ce te se morate potrudit jos bolje. Malo vise Cokolina nije nikad nikoga ubilo, iako sam cuo za skoro smrtni slucaj od predoziranja Cokolinom. Ali sve je bilo dobro, lik je sada ziv i zdrav, pise po forumu, predaje zadace redovito itd. :) I dalje stavlja jako malo mlijeka u jako puno Cokolina.
P.S.
[quote="Ilja"]Ej cima, znaš li kog sam sreo vani večeras, našeg pravog sugovornika, uvaženog Periciusa.[/quote]
Ocito nam je bilo strasno zabavno (i uspjesno) obojici kada opet visimo po forumu. :lol:
[size=9][color=green]np: ma who cares, vise necu ni pisat ovo malo glupo zeleno[/color][/size]
Nisu vas zalockali!?
Hmm, izgleda da ce te se morate potrudit jos bolje. Malo vise Cokolina nije nikad nikoga ubilo, iako sam cuo za skoro smrtni slucaj od predoziranja Cokolinom. Ali sve je bilo dobro, lik je sada ziv i zdrav, pise po forumu, predaje zadace redovito itd.  I dalje stavlja jako malo mlijeka u jako puno Cokolina. I dalje stavlja jako malo mlijeka u jako puno Cokolina.
P.S.
| Ilja (napisa): | | Ej cima, znaš li kog sam sreo vani večeras, našeg pravog sugovornika, uvaženog Periciusa. |
Ocito nam je bilo strasno zabavno (i uspjesno) obojici kada opet visimo po forumu. 
np: ma who cares, vise necu ni pisat ovo malo glupo zeleno
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vjakovac
Forumaš s poteškoćama u pisanju

Pridružen/a: 28. 02. 2006. (10:07:16)
Postovi: (4B)16
|
 Postano: 12:14 sub, 22. 4. 2006 Naslov: Re: pomoc oko zadataka Postano: 12:14 sub, 22. 4. 2006 Naslov: Re: pomoc oko zadataka |
    |
|
|
[quote="sun"]a o čemu to ovisi, mislim to me zbunilo zato što smo mi na vježbama napisali otvorene intervale(a je mislim da su na nekim mjestima trebali ići zatvoreni. )i sad vidim da je ilja stavio sve zatvorene[/quote]
Nisam uopće bio shvatio o kakvim intervalima se radilo u pitanju pa sam odgovorio tek tako.
Ilja i ja smo se upravo složili da je sasvim svejedno zovemo li intervalima rasta i pada uvijek otvorene intervale ili radije pišemo zatvorene intervale.
Sve funkcije za koje uopće ima smisla gledati intervale rasta i pada (npr. Dirichletova funkcija ni na kojem intervalu niti raste niti pada pa za nju nema smisla govoriti o intervalima rasta i pada) su takve da je R s konačno mnogo točaka podijeljen na intervale na kojima derivacija funkcije ima konstantan predznak (tj. ili je >0 ili je <0) i na svakom tom zatvorenom intervalu funkcija strogo raste ili strogo pada.
Jedino što bi možda bilo krivo je napisati da funkcija (strogo) raste na [2,4] ako broj 2 uopće nije u domeni funkcije ili ako funkcija ima prekid u točki 2 [size=7](zaboravih Hvala Ilja)[/size]. Tada bismo napisali da funkcija (strogo) raste na <2,4] ili da ne kompliciramo na <2,4>.
[b]Ukratko: svejedno je. Ako ne želimo paziti, možemo uvijek pisati otvorene intervale, nije krivo. [/b]
___________________
I prof. Folland se slaže. 8)
| sun (napisa): | | a o čemu to ovisi, mislim to me zbunilo zato što smo mi na vježbama napisali otvorene intervale(a je mislim da su na nekim mjestima trebali ići zatvoreni. )i sad vidim da je ilja stavio sve zatvorene |
Nisam uopće bio shvatio o kakvim intervalima se radilo u pitanju pa sam odgovorio tek tako.
Ilja i ja smo se upravo složili da je sasvim svejedno zovemo li intervalima rasta i pada uvijek otvorene intervale ili radije pišemo zatvorene intervale.
Sve funkcije za koje uopće ima smisla gledati intervale rasta i pada (npr. Dirichletova funkcija ni na kojem intervalu niti raste niti pada pa za nju nema smisla govoriti o intervalima rasta i pada) su takve da je R s konačno mnogo točaka podijeljen na intervale na kojima derivacija funkcije ima konstantan predznak (tj. ili je >0 ili je <0) i na svakom tom zatvorenom intervalu funkcija strogo raste ili strogo pada.
Jedino što bi možda bilo krivo je napisati da funkcija (strogo) raste na [2,4] ako broj 2 uopće nije u domeni funkcije ili ako funkcija ima prekid u točki 2 (zaboravih Hvala Ilja). Tada bismo napisali da funkcija (strogo) raste na <2,4] ili da ne kompliciramo na <2,4>.
Ukratko: svejedno je. Ako ne želimo paziti, možemo uvijek pisati otvorene intervale, nije krivo.
___________________
I prof. Folland se slaže. 
Zadnja promjena: vjakovac; 12:24 sub, 22. 4. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 12:17 sub, 22. 4. 2006 Naslov: Re: pomoc oko zadataka Postano: 12:17 sub, 22. 4. 2006 Naslov: Re: pomoc oko zadataka |
    |
|
|
[quote="sun"]Meni numerički ispada [-33,31].
i meni tako ispada
hvala vjeko
[/quote]
bitni su kakvi su[/quote]
a o čemu to ovisi, mislim to me zbunilo zato što smo mi na vježbama napisali otvorene intervale(a je mislim da su na nekim mjestima trebali ići zatvoreni. )i sad vidim da je ilja stavio sve zatvorene
help vjeko[/quote]
Ako je funkcija definirana na nekom intervalu "dovoljno lijepa" (a takve su bile (gotovo) sve funkcije koje smo imali na vježbama uz gradivo oko rasta/pada) onda će derivacija imati eventualno konačno mnogo nultočki, bit će neprekidna, što znači da će na intervalima određenim tim nultočkama derivacije biti stalnog predznaka. Znači za svaku točku domene će postojat najveći zatvoreni / otvoreni interval koji ju sadrži i da je restrikcija od f na taj zatvoreni/otvoreni interval stogo rastuća (padajuća). Ukratko, možeš uzeti bilo otv. bilo zatv. i sve je ok.
Da to općenito nije tako, pogledaj npr. funkciju [latex]f: [0,1] \rightarrow \mathbb{R}[/latex] def. formulom
[latex]f(x):=\left\{\begin{array}{ll}
x &: 0 \leq x <1\\
-1 & : x=1
\end{array}\right. [/latex]
Ona je svakako strogo rastuća na [latex]\langle 0,1 \rangle[/latex], ali nije na [latex][0,1][/latex], pa je tu bitno koji interval uzmeš. No ta funkcija ima prekid u 1, pa nije dovoljno lijepa.
[b]Edit:[/b] Eto, sad smo ti obojica napisali isto, to je dobro.
| sun (napisa): | Meni numerički ispada [-33,31].
i meni tako ispada
hvala vjeko
|
bitni su kakvi su[/quote]
a o čemu to ovisi, mislim to me zbunilo zato što smo mi na vježbama napisali otvorene intervale(a je mislim da su na nekim mjestima trebali ići zatvoreni. )i sad vidim da je ilja stavio sve zatvorene
help vjeko[/quote]
Ako je funkcija definirana na nekom intervalu "dovoljno lijepa" (a takve su bile (gotovo) sve funkcije koje smo imali na vježbama uz gradivo oko rasta/pada) onda će derivacija imati eventualno konačno mnogo nultočki, bit će neprekidna, što znači da će na intervalima određenim tim nultočkama derivacije biti stalnog predznaka. Znači za svaku točku domene će postojat najveći zatvoreni / otvoreni interval koji ju sadrži i da je restrikcija od f na taj zatvoreni/otvoreni interval stogo rastuća (padajuća). Ukratko, možeš uzeti bilo otv. bilo zatv. i sve je ok.
Da to općenito nije tako, pogledaj npr. funkciju 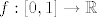 def. formulom def. formulom
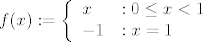
Ona je svakako strogo rastuća na 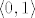 , ali nije na , ali nije na 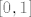 , pa je tu bitno koji interval uzmeš. No ta funkcija ima prekid u 1, pa nije dovoljno lijepa. , pa je tu bitno koji interval uzmeš. No ta funkcija ima prekid u 1, pa nije dovoljno lijepa.
Edit: Eto, sad smo ti obojica napisali isto, to je dobro.
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
vjakovac
Forumaš s poteškoćama u pisanju


Pridružen/a: 28. 02. 2006. (10:07:16)
Postovi: (4B)16
|
 Postano: 12:30 sub, 22. 4. 2006 Naslov: Re: zadatak Postano: 12:30 sub, 22. 4. 2006 Naslov: Re: zadatak |
    |
|
|
[quote="Anonymous"]Nadjite intervale rasta i pada te lokalne ekstreme funkcije f:<0,+oo>-->R, f(x)=x^1/x. pliz neka mi netko rijesi![/quote]
[latex]f(x)=e^{\frac{\ln x}{x}}[/latex]
[latex]f'(x)=e^{\frac{\ln x}{x}}\cdot\frac{1-\ln x}{x^2}[/latex]
f strogo raste na [latex]\langle 0,e][/latex], a strogo pada na [latex][e,+\infty\rangle[/latex].
Ima lokalni maksimum u točki e, koji iznosi f(e)=e^(1/e).
[quote="sun"]karma++[/quote]
Da mi je znat kako ćeš Ilji dat karmu. :-s :lol:
| Anonymous (napisa): | | Nadjite intervale rasta i pada te lokalne ekstreme funkcije f:<0,+oo>→R, f(x)=x^1/x. pliz neka mi netko rijesi! |
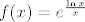

f strogo raste na 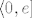 , a strogo pada na , a strogo pada na 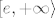 . .
Ima lokalni maksimum u točki e, koji iznosi f(e)=e^(1/e).
Da mi je znat kako ćeš Ilji dat karmu.  
Zadnja promjena: vjakovac; 12:33 sub, 22. 4. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 12:31 sub, 22. 4. 2006 Naslov: Re: zadatak Postano: 12:31 sub, 22. 4. 2006 Naslov: Re: zadatak |
    |
|
|
[quote="Anonymous"]Nadjite intervale rasta i pada te lokalne ekstreme funkcije f:<0,+oo>-->R, f(x)=x^1/x. pliz neka mi netko rijesi![/quote]
Evo ti uputa [latex]f(x)=e^{1/x \ln x}[/latex], pa je [latex]f'(x)=f(x)\cdot (-1/x^2 \ln x + 1/x^2)[/latex]. Kako je [latex]1/x^2 \cdot f(x)>0 \ \forall x \in \langle 0, +\infty \rangle [/latex], predznak derivacije ovisi samo o predznaku od [latex](1- \ln x)[/latex], pa [latex]f[/latex] stogo raste na [latex]\langle 0, e \rangle[/latex], odn. strogo pada na [latex]\langle e , + \infty \rangle[/latex].
[b]Edit:[/b] Pa Kovaču daj se skuliraj malo. Nema veze i dalje te volim :konj:
P.S. [quote="Žuti"] Ilja ako nije bed i mi bi se skrpali za podršku da se topic ne zaključa. Živjela Tesla i svi ostali [/quote]
Ma nema beda buraz. 8) Tako je, živio i sam Tesla!!! :idea:
| Anonymous (napisa): | | Nadjite intervale rasta i pada te lokalne ekstreme funkcije f:<0,+oo>→R, f(x)=x^1/x. pliz neka mi netko rijesi! |
Evo ti uputa 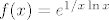 , pa je , pa je 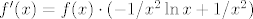 . Kako je . Kako je 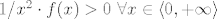 , predznak derivacije ovisi samo o predznaku od , predznak derivacije ovisi samo o predznaku od 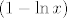 , pa , pa  stogo raste na stogo raste na 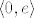 , odn. strogo pada na , odn. strogo pada na 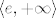 . .
Edit: Pa Kovaču daj se skuliraj malo. Nema veze i dalje te volim 
P.S. | Žuti (napisa): | | Ilja ako nije bed i mi bi se skrpali za podršku da se topic ne zaključa. Živjela Tesla i svi ostali |
Ma nema beda buraz.  Tako je, živio i sam Tesla!!! Tako je, živio i sam Tesla!!! 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 14:42 sub, 22. 4. 2006 Naslov: Postano: 14:42 sub, 22. 4. 2006 Naslov: |
    |
|
|
[color=darkred]Ovaj put necu lockati jer se cini da ste se malo vratili temi topica. :roll:
Za ubuduce:
1. Zaspammani topici se lockaju. :evil:
2. Spammerski accounti ce takodjer biti pozakljucavani (ukljucujuci i asistentske). :evil:
3. Budete li i dalje radili gluposti s gost accountima, gosti vise nece imati write-pristup na podforum MA1&2. :evil:
4. Ako i dalje asistenti Analize budu problem ili se pretjera sa spammom, zalockat cu cijeli MA1&2 podforum. :evil:
Ako netko ima prigovor, neka mi ga kaze u facu. :P Ovaj post je javno upozorenje, a ne poziv na raspravu; svaki nastavak te price smatrat cu spammom, na sto - kao voditelj Foruma - imam pravo. :P[/color]
Ovaj put necu lockati jer se cini da ste se malo vratili temi topica. 
Za ubuduce:
1. Zaspammani topici se lockaju. 
2. Spammerski accounti ce takodjer biti pozakljucavani (ukljucujuci i asistentske). 
3. Budete li i dalje radili gluposti s gost accountima, gosti vise nece imati write-pristup na podforum MA1&2. 
4. Ako i dalje asistenti Analize budu problem ili se pretjera sa spammom, zalockat cu cijeli MA1&2 podforum. 
Ako netko ima prigovor, neka mi ga kaze u facu.  Ovaj post je javno upozorenje, a ne poziv na raspravu; svaki nastavak te price smatrat cu spammom, na sto - kao voditelj Foruma - imam pravo. Ovaj post je javno upozorenje, a ne poziv na raspravu; svaki nastavak te price smatrat cu spammom, na sto - kao voditelj Foruma - imam pravo. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 16:14 sub, 22. 4. 2006 Naslov: Postano: 16:14 sub, 22. 4. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]Bok!evo jos dva zadatka pa ako neko ima volje bila bi mu zahvalna da ih rijesi:
1.Ukojim tockama skupa R postoji n-ta derivacija (n E N) funkcije zadane formulom f(x)=aps(x)*sinx .Izracunaj f^(100)(x).
2.Odredi globalne ekstreme funkcije f(x)=arccos(sinx) na[-pi ,pi].[/quote]
Bok i tebi! :)
1. Ako stavimo [latex]\mathbb{R}^*=\mathbb{R} \ \setminus \{0\}[/latex], onda je svakako [latex] f \in C^{\infty}(\mathbb{R}^*)[/latex] i imamo
[latex]f'(x)=\left\{\begin{array}{ll}
-\sin x - x \cos x &: x < 0\\
\sin x + x \cos x & : x>0
\end{array}\right. [/latex].
Budući je [latex]\lim_{x \rightarrow 0^-} f'(x)=\lim_{x \rightarrow 0^+} f'(x)=0[/latex], [latex]f[/latex] je također derivabilna i u [latex]0[/latex] i derivacija od f je neprekidna u [latex]0[/latex].
Znači [latex]f \in C^{1}(\mathbb{R}) \cap C^{\infty}(\mathbb{R}^*)[/latex] i u gornjoj formuli za derivaciju možemo uključiti i 0, tj.
[latex]f'(x)=\left\{\begin{array}{ll}
-\sin x - x \cos x &: x \leq 0\\
\sin x + x \cos x & : x>0
\end{array}\right. [/latex].
No [latex]f''(0):=\lim_{h \rightarrow 0}\frac{f'(h)-f'(0)}{h}[/latex] ne postoji, jer se jednostrani limesi ne podudaraju: [latex]\lim_{h \rightarrow 0^-}\frac{f'(h)-f'(0)}{h}=\lim_{h \rightarrow 0^-}\frac{-\sin h - h \cos h}{h}=-2[/latex], a [latex]\lim_{h \rightarrow 0^+}\frac{f'(h)-f'(0)}{h}=\lim_{h \rightarrow 0^+}\frac{\sin h + h \cos h}{h}=2[/latex].
I na kraju iz Leibnizove formule slijedi da je
[latex]f^{(n)}(x)=\left\{\begin{array}{ll}
- x\sin(x + \frac{n \pi}{2})-n\sin(x + \frac{(n-1) \pi}{2}) &: x < 0\\
x\sin(x + \frac{n \pi}{2})+n\sin(x + \frac{(n-1) \pi}{2}) & : x>0
\end{array}\right.[/latex]
za sve [latex]n \in \mathbb{N}[/latex].
[b]2[/b]. Ovo mi je malo čudno da je zadatak iz ma2, jer tu ne treba nigdje koristiti diferencijalni račun. :?
Kako je [latex]0\leq\arccos x \leq \pi , \forall x \in [-1,1][/latex], to je i [latex]0\leq\arccos(\sin x)\leq \pi , \forall x \in \mathbb{R} [/latex]. Budući su [latex]-\frac{\pi}{2} , \frac{\pi}{2} \in [-\pi, \pi] [/latex] i [latex]\arccos(\sin (-\frac{\pi}{2}))=\pi[/latex] odn. [latex]\arccos(\sin \frac{\pi}{2})=0[/latex], a kako je [latex]|\sin x| \neq 1[/latex] na [latex][-\pi, \pi]\setminus \{-\frac{\pi}{2},\frac{\pi}{2}\}[/latex], to su baš to svi globalni ekstremi od [latex]f[/latex] na[latex][-\pi, \pi][/latex].
[quote="Anonymous"]
htjela bi pitati ako je netko rjesio 3. zadatak pod b) ?
ja sam dodefinirala f-ju pa mi ispada 12 za x=0 [/quote]
Dobro ti je ispalo. :)
| Anonymous (napisa): | Bok!evo jos dva zadatka pa ako neko ima volje bila bi mu zahvalna da ih rijesi:
1.Ukojim tockama skupa R postoji n-ta derivacija (n E N) funkcije zadane formulom f(x)=aps(x)*sinx .Izracunaj f^(100)(x).
2.Odredi globalne ekstreme funkcije f(x)=arccos(sinx) na[-pi ,pi]. |
Bok i tebi! 
1. Ako stavimo 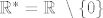 , onda je svakako , onda je svakako 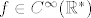 i imamo i imamo
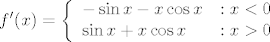 . .
Budući je 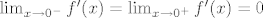 , ,  je također derivabilna i u je također derivabilna i u  i derivacija od f je neprekidna u i derivacija od f je neprekidna u  . .
Znači 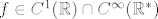 i u gornjoj formuli za derivaciju možemo uključiti i 0, tj. i u gornjoj formuli za derivaciju možemo uključiti i 0, tj.
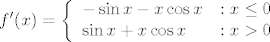 . .
No 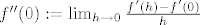 ne postoji, jer se jednostrani limesi ne podudaraju: ne postoji, jer se jednostrani limesi ne podudaraju: 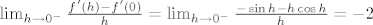 , a , a 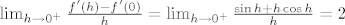 . .
I na kraju iz Leibnizove formule slijedi da je
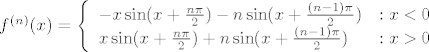
za sve  . .
2. Ovo mi je malo čudno da je zadatak iz ma2, jer tu ne treba nigdje koristiti diferencijalni račun. 
Kako je  , to je i , to je i 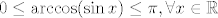 . Budući su . Budući su 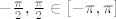 i i 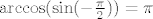 odn. odn. 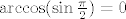 , a kako je , a kako je 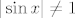 na na 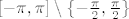 , to su baš to svi globalni ekstremi od , to su baš to svi globalni ekstremi od  na na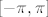 . .
| Anonymous (napisa): |
htjela bi pitati ako je netko rjesio 3. zadatak pod b) ?
ja sam dodefinirala f-ju pa mi ispada 12 za x=0 |
Dobro ti je ispalo. 
|
|
| [Vrh] |
|
zzsan
Forumaš(ica)

Pridružen/a: 25. 11. 2005. (20:53:14)
Postovi: (89)16
|
|
| [Vrh] |
|
vanish
Forumaš(ica)


Pridružen/a: 02. 10. 2005. (22:45:35)
Postovi: (6D)16
Spol: 
Lokacija: stambena zgrada
|
|
| [Vrh] |
|
vjakovac
Forumaš s poteškoćama u pisanju


Pridružen/a: 28. 02. 2006. (10:07:16)
Postovi: (4B)16
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|












