| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 11:05 ned, 30. 4. 2006 Naslov: Postano: 11:05 ned, 30. 4. 2006 Naslov: |
    |
|
|
U tom teoremu prvi smjer vrijedi općenito i u topološkim prostorima. Ako su X i Y topološki prostori, f:X->Y neprekidno preslikavanje u točki P*@X te ako niz (P_k) u X konvergira prema P*, onda (f(P_k)) u Y konvergira prema f(P*).
Naime, u dokazu navedenom u knjizi na str. 39 lako se korištenje metrike može zaobići korištenjem otvorenih okolina točaka.
No, u dokazu obrata to baš ne ide. Metrika je ono na što se oslanjamo da konstruiramo niz u Y koji nikako ne može konvergirati prema f(P*). To možda nije dovoljno dobar argument da kažemo da obrat općenito ne vrijedi u topološkim prostorima jer bi trebalo naći protuprimjer, ali mislim da bi time izašli izvan opsega razmatranja topologije predviđenog za naš predmet.
Inače, koga zanima, ovo je razjašnjeno u knjizi Matematička analiza 1 Sibe Mardešića. :wink:
U tom teoremu prvi smjer vrijedi općenito i u topološkim prostorima. Ako su X i Y topološki prostori, f:X->Y neprekidno preslikavanje u točki P*@X te ako niz (P_k) u X konvergira prema P*, onda (f(P_k)) u Y konvergira prema f(P*).
Naime, u dokazu navedenom u knjizi na str. 39 lako se korištenje metrike može zaobići korištenjem otvorenih okolina točaka.
No, u dokazu obrata to baš ne ide. Metrika je ono na što se oslanjamo da konstruiramo niz u Y koji nikako ne može konvergirati prema f(P*). To možda nije dovoljno dobar argument da kažemo da obrat općenito ne vrijedi u topološkim prostorima jer bi trebalo naći protuprimjer, ali mislim da bi time izašli izvan opsega razmatranja topologije predviđenog za naš predmet.
Inače, koga zanima, ovo je razjašnjeno u knjizi Matematička analiza 1 Sibe Mardešića. 
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 11:22 ned, 30. 4. 2006 Naslov: Postano: 11:22 ned, 30. 4. 2006 Naslov: |
    |
|
|
Ajde, da ne ostane nedorečeno, napisat ću što to piše u knjizi ak. Mardešića.
Neka je X neprebrojiv skup. Neka je U topologija koja se sastoji od praznog skupa i komplemenata prebrojivih podskupova od X, a neka je V partitivni skup od X (tzv. [i]diskretna topologija[/i]). Treba dokazati da identiteta [i]i[/i] iz (X,U) u (X,V) nije neprekidno preslikavanje iako za svaki niz (x_n) iz X konvergencija prema x_0 s obzirom na U povlači konvergenciju s obzirom na V.
Ovaj primjer je zanimljiv i stoga što vidimo da identiteta ne mora biti neprekidno preslikavanje. :?
Pozdrav
Ajde, da ne ostane nedorečeno, napisat ću što to piše u knjizi ak. Mardešića.
Neka je X neprebrojiv skup. Neka je U topologija koja se sastoji od praznog skupa i komplemenata prebrojivih podskupova od X, a neka je V partitivni skup od X (tzv. diskretna topologija). Treba dokazati da identiteta i iz (X,U) u (X,V) nije neprekidno preslikavanje iako za svaki niz (x_n) iz X konvergencija prema x_0 s obzirom na U povlači konvergenciju s obzirom na V.
Ovaj primjer je zanimljiv i stoga što vidimo da identiteta ne mora biti neprekidno preslikavanje. 
Pozdrav
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 12:47 ned, 30. 4. 2006 Naslov: Postano: 12:47 ned, 30. 4. 2006 Naslov: |
    |
|
|
Ovo je baš dobar primjer, a čini mi se da ću dodati još par filozofskih napomena :D
Kod tog topološkog prostora je problem što imamo više "bitnih" (tzv. baznih) okolina oko točke nego što ima prirodnih brojeva. Npr. ako je [latex]X[/latex] metrički prostor, onda oko svake dočke imamo prebrojivo mnogo baznih okolina, tj. za svaku točku [latex]x \in X[/latex] i njenu okolinu [latex]U[/latex] postoji [latex]n \in \mathbb{N}[/latex] td. je kugla [latex]K(x, \frac{1}{n})\subseteq U[/latex]. To se šminkerski kaže da familija kugala [latex]\{K(x, \frac{1}{n}): n \in \mathbb{N}\ \}[/latex] tvori [i]bazu okolina[/i] točke [latex]x[/latex]. Znači da kod metričkih prostora svaka točka ima prebrojivu bazu okolina, ili kraće da metrički prosotri zadovoljavaju [i]prvi aksiom prebrojivosti[/i] i upravo nam to osigurava nizovnu karakterizaciju neprekidnosti (na nivou metričkih prostora).
U slučaju topološkog prostora koji ne zadovoljava prvi aksiom prebrojivosti (specijalno taj nije metrizabilan), kao što je ovaj iz gornjeg primjera, nizovna karakterizacija neprekidnosti neće biti dovoljna, jer nećemo imati prebrojivo baznih okolina oko neke točke. No tu onda prelazimo na tzv. generalizirane nizove (tzv. [i]hipernizove[/i], odn. [i]mreže[/i]), pa i dalje dobivamo tzv. "mrežovnu" karakterizaciju neprekidnosti. No o tome ćete više čuti na kolegiju Metrički prostori. :D
[quote="LSSD"]E sad me zanima da li Heineova karakterizacija neprekidnosti vrijedi za topoloske prostore?Ja bih rekla da ne jer tamo ne mozemo govoriti o jedinstvenosti limesa, samo me zanima da li je ta argumentacija dobra?[/quote]
To je istina da kod općenitog topološkog prostora limes niza (mreže) ne mora biti jedinstven (ni takav prostor nije metrizabilan), no to nije pravi razlog zašto ne prolazi Heineova karakterizacija neprekidnosti, ona pada baš zbog ovog gore napisanog.
Ovo je baš dobar primjer, a čini mi se da ću dodati još par filozofskih napomena 
Kod tog topološkog prostora je problem što imamo više "bitnih" (tzv. baznih) okolina oko točke nego što ima prirodnih brojeva. Npr. ako je  metrički prostor, onda oko svake dočke imamo prebrojivo mnogo baznih okolina, tj. za svaku točku metrički prostor, onda oko svake dočke imamo prebrojivo mnogo baznih okolina, tj. za svaku točku  i njenu okolinu i njenu okolinu 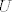 postoji postoji  td. je kugla td. je kugla 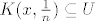 . To se šminkerski kaže da familija kugala . To se šminkerski kaže da familija kugala 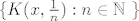 tvori bazu okolina točke tvori bazu okolina točke  . Znači da kod metričkih prostora svaka točka ima prebrojivu bazu okolina, ili kraće da metrički prosotri zadovoljavaju prvi aksiom prebrojivosti i upravo nam to osigurava nizovnu karakterizaciju neprekidnosti (na nivou metričkih prostora). . Znači da kod metričkih prostora svaka točka ima prebrojivu bazu okolina, ili kraće da metrički prosotri zadovoljavaju prvi aksiom prebrojivosti i upravo nam to osigurava nizovnu karakterizaciju neprekidnosti (na nivou metričkih prostora).
U slučaju topološkog prostora koji ne zadovoljava prvi aksiom prebrojivosti (specijalno taj nije metrizabilan), kao što je ovaj iz gornjeg primjera, nizovna karakterizacija neprekidnosti neće biti dovoljna, jer nećemo imati prebrojivo baznih okolina oko neke točke. No tu onda prelazimo na tzv. generalizirane nizove (tzv. hipernizove, odn. mreže), pa i dalje dobivamo tzv. "mrežovnu" karakterizaciju neprekidnosti. No o tome ćete više čuti na kolegiju Metrički prostori. 
| LSSD (napisa): | | E sad me zanima da li Heineova karakterizacija neprekidnosti vrijedi za topoloske prostore?Ja bih rekla da ne jer tamo ne mozemo govoriti o jedinstvenosti limesa, samo me zanima da li je ta argumentacija dobra? |
To je istina da kod općenitog topološkog prostora limes niza (mreže) ne mora biti jedinstven (ni takav prostor nije metrizabilan), no to nije pravi razlog zašto ne prolazi Heineova karakterizacija neprekidnosti, ona pada baš zbog ovog gore napisanog.
|
|
| [Vrh] |
|
|








