|
[quote="Wuvie"]
Dokažite da vrijedi
[latex]A\setminus(B\cup C)\subseteq(A\setminus B)\cup(A\cap C)[/latex].
Jednakost vrijedi onda i samo onda ako je [latex]A\cap C=\emptyset[/latex].
[/quote]
ovak; prvo nejednakost:
neka je x iz A\(BuC); otud imas da je x iz A i da x nije iz BuC; e, sad..to, prema def.unije i kad negiras, znaci da je x iz A, da x nije iz B i da x nije iz C; pa to specijalno znaci i da je x iz A\B, pa je i iz A\B uniran s bilo cim, pa specijalno i sa A"presjek"C, i dobijes da je x u desnoj strani;
sad jednakost; dokazujemo da vrijedi jednakost navedenih skupova <=> A"presjek"C=prazan skup;
ajmo dokazat =>:
pa..pretp.suprotno; neka postoji neki x iz A"presjek"C; to dalje povlaci da je x iz (A"presjek"C)u(A\B), a taj je skup jednak skupu A\(BuC), pa znaci da je x i iz njega...ali, onda dobijemo da je x u A, da nije u B i da nije u C...sto je kontradikcija s pocetnom pretp.da je x iz A"presjek"C;
i jos <=:
da je lijeva strana podskup od desne...to vrijedi opcenito, pa i u ovom slucaju...
da je desna strana podskup od lijeve:
pa neka je x iz (A\B)u(A"presjek"C)=A\B; jer je A"presjek"C prazan skup...e, sada...
prvi slucaj; ako x nije iz C, dobijemo da je x u A i da nije u BuC...sto smo i tocno trebali..
drugi slucaj; ako je x u C, dobijemo da je x iz A"presjek"C , a to znaci da je x iz praznog skupa, sto je kontradikcija
etoga....hope this helps :wink:
| Wuvie (napisa): |
Dokažite da vrijedi
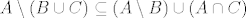 . .
Jednakost vrijedi onda i samo onda ako je 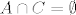 . .
|
ovak; prvo nejednakost:
neka je x iz A\(BuC); otud imas da je x iz A i da x nije iz BuC; e, sad..to, prema def.unije i kad negiras, znaci da je x iz A, da x nije iz B i da x nije iz C; pa to specijalno znaci i da je x iz A\B, pa je i iz A\B uniran s bilo cim, pa specijalno i sa A"presjek"C, i dobijes da je x u desnoj strani;
sad jednakost; dokazujemo da vrijedi jednakost navedenih skupova ⇔ A"presjek"C=prazan skup;
ajmo dokazat ⇒:
pa..pretp.suprotno; neka postoji neki x iz A"presjek"C; to dalje povlaci da je x iz (A"presjek"C)u(A\B), a taj je skup jednak skupu A\(BuC), pa znaci da je x i iz njega...ali, onda dobijemo da je x u A, da nije u B i da nije u C...sto je kontradikcija s pocetnom pretp.da je x iz A"presjek"C;
i jos ⇐:
da je lijeva strana podskup od desne...to vrijedi opcenito, pa i u ovom slucaju...
da je desna strana podskup od lijeve:
pa neka je x iz (A\B)u(A"presjek"C)=A\B; jer je A"presjek"C prazan skup...e, sada...
prvi slucaj; ako x nije iz C, dobijemo da je x u A i da nije u BuC...sto smo i tocno trebali..
drugi slucaj; ako je x u C, dobijemo da je x iz A"presjek"C , a to znaci da je x iz praznog skupa, sto je kontradikcija
etoga....hope this helps 
_________________ Laganini...i stprljivo....  |





