|
Hm. Tako napisano baš i ne vrijedi, jer ako je [latex]f[/latex] konstantna funkcija različita od nul-funkcije onda ona zadovoljava uvjete zadatka, ali ta nema nultočki.
Uz dodatnu pretpostavku da [latex]f[/latex] nije konstanta možemo ovako dokazati
Pretpostavimo suprotno, tj. da je [latex]f(z) \neq 0, \ \forall z \in U[/latex].
Ukoliko je [latex]f(z_0)=0[/latex] za neko [latex]z_0 \in \partial U [/latex], onda je po pretpostavci zadatka i [latex]f(z)=0, \ \forall z \in \partial U[/latex], što je kontradiktorno principu maksimuma modula, budući bi onda moralo biti [latex]|f(z)|<0, \ \forall z \in U[/latex], što je nemoguće.
Ako je pak [latex]f(z) \neq 0, \ \forall z \in \partial U[/latex], onda stavimo
[latex]0<M:=|f(z)|, \ z \in \partial U[/latex] i [latex]g(z):= \frac{f(z)}{M},\ z \in \overline{U} [/latex]. Tada je [latex]g[/latex] holomorfna na [latex]U[/latex] i neprekidna na [latex]\overline{U}[/latex].
(Broj [latex]M[/latex] ne ovisi o izboru točke [latex]z \in \partial U[/latex]).
Po principu maksimuma modula slijedi da je [latex]|g(z)| \leq 1, \ \forall z \in \overline{U}[/latex], a budući je i funkcija [latex]z \mapsto \frac{1}{g(z)}[/latex] holomorfna na [latex]U[/latex] i neprekidna na [latex]\overline{U}[/latex], to ponovo iz principa max. modula slijedi da je [latex]\frac{1}{|g(z)|}\leq 1, \ \forall z \in \overline{U}[/latex]. Znači da je [latex]|g(z)|=1, \ \forall z \in \overline{U}[/latex] što povlači da je [latex]g[/latex] konstanta (jer bi u protivnom (ponovo po princ. max. modula) bilo [latex]1=|g(z)|<1, \ \forall z \in U[/latex]), pa je i [latex]f[/latex] konstanta, što je protivno pretpostavci.
Eto. :D
Hm. Tako napisano baš i ne vrijedi, jer ako je  konstantna funkcija različita od nul-funkcije onda ona zadovoljava uvjete zadatka, ali ta nema nultočki. konstantna funkcija različita od nul-funkcije onda ona zadovoljava uvjete zadatka, ali ta nema nultočki.
Uz dodatnu pretpostavku da  nije konstanta možemo ovako dokazati nije konstanta možemo ovako dokazati
Pretpostavimo suprotno, tj. da je 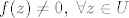 . .
Ukoliko je 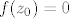 za neko za neko 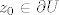 , onda je po pretpostavci zadatka i , onda je po pretpostavci zadatka i 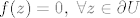 , što je kontradiktorno principu maksimuma modula, budući bi onda moralo biti , što je kontradiktorno principu maksimuma modula, budući bi onda moralo biti 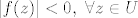 , što je nemoguće. , što je nemoguće.
Ako je pak 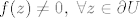 , onda stavimo , onda stavimo
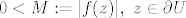 i i 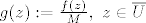 . Tada je . Tada je  holomorfna na holomorfna na 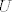 i neprekidna na i neprekidna na 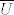 . .
(Broj  ne ovisi o izboru točke ne ovisi o izboru točke 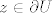 ). ).
Po principu maksimuma modula slijedi da je 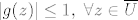 , a budući je i funkcija , a budući je i funkcija 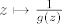 holomorfna na holomorfna na 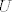 i neprekidna na i neprekidna na 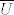 , to ponovo iz principa max. modula slijedi da je , to ponovo iz principa max. modula slijedi da je 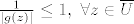 . Znači da je . Znači da je 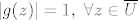 što povlači da je što povlači da je  konstanta (jer bi u protivnom (ponovo po princ. max. modula) bilo konstanta (jer bi u protivnom (ponovo po princ. max. modula) bilo 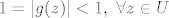 ), pa je i ), pa je i  konstanta, što je protivno pretpostavci. konstanta, što je protivno pretpostavci.
Eto. 
|




