|
[quote][b]Dokaz:[/b]Najprije primijetimo da se [latex]\delta(\alpha)[/latex] mijenja samo ako [latex]\alpha[/latex] prolazi kroz nultočku neke od derivacija [latex]f^{(i)}[/latex]. [i][color=red](Evo ja već ne razumijem zašto mora prolaziti? I što znači da [latex]\alpha[/latex] prolazi kroz nultočku?)[/color][/i].[/quote]
Hoce se reci: uzmimo da je [latex]\alpha[/latex] na pocetku jednak jednom kraju intervala [latex]\[a,b\][/latex], te ga pustimo da putuje prema drugom kraju -- shvati to kao "autoinkrement" (odnosno, "autodekrement") od [latex]\alpha[/latex], kad bi takvo sto u [latex]\mathbb{R}[/latex] bilo moguce definirati. Dakle, ako u tom intervalu postoji nultocka polinoma [latex]f[/latex], [latex]\alpha[/latex] mora kroz nju proci.
[quote]Da bismo izračunali broj promjena predznaka, razlikujemo dva slučaja:
(i) [latex]\alpha[/latex] je nultočka od f kratnosti m. U tom slučaju [latex]f(\alpha)=\cdots=f^{(m-1)}(\alpha)=0, f^{(m)}(\alpha)\neq 0[/latex]. Prema Taylorovoj formuli:
[latex]\displaystyle f(\alpha+h)=\frac{f^{(m)}(\alpha)}{m!}h^m+\ldots,\\ f'(\alpha+h)=\frac{f^{(m)}(\alpha)}{(m-1)!}h^{m-1}+\ldots,\\ \ldots\ldots\ldots=\ldots\ldots\ldots\ldots\ldots\ldots\ldots\\ \ldots\ldots\ldots=\ldots\ldots\ldots\ldots\ldots\ldots\ldots\\ \ldots\ldots\ldots=\ldots\ldots\ldots\ldots\ldots\ldots\ldots\\ f^{(m)}(\alpha+h)=f^{(m)}(\alpha)+\ldots[/latex].
Za dovoljno malo h izrazi napisani na desnim stranama ovih jednakosti dominantni su [i][color=red](Što to znači da su dominantni?)[/color][/i][/quote]
[i]Vjerojatno[/i] se misli na to da prvi ne-nul clan Taylorovog reda, uz uvjet da je [latex]h[/latex] "dovoljno mali", po modulu dominira nad ostatkom reda.
[quote]i ako h prolazi s [b]pozitivnih na negativne[/b] vrijednosti, broj promjena predznaka u podnizu [latex]f,f',\ldots,f^{(m)}[/latex] niza (*) jest m [i][color=red](Što znači da h prolazi s pozitivnih na negativne vrijednosti? I zašto je baš m promjena predznaka?)[/color][/i],[/quote]
Primijeti koliko je vazan smjer u kojem [latex]h[/latex] mijenja vrijednosti, odnosno gleda se okolina od [latex]\alpha[/latex] s desna na lijevo. Parne potencije od [latex]h[/latex], bio [latex]h[/latex] pozitivan ili negativan, daju pozitivne vrijednosti, dok neparne potencije za negativni [latex]h[/latex] daju negativne vrijednosti. Sad malo upogoni mastu (a.k.a. olovku) i vidjet ces da je broj promjena predznaka kroz [latex]\alpha[/latex] upravo [latex]m[/latex]. (Svaka negativna vrijednost generira po jednu promjenu predznaka sa svakim susjedom.)
[quote]a taj se broj podudara i s brojem prijeđenih nultočaka.[i][color=red](Koje su to prijeđene nultočke i zašto se ti brojevi podudaraju?)[/color][/i].[/quote]
Mozda je problem u nepreciznoj formulaciji teorema: kad se spominje broj nultocki, misli se na njihovu kratnost (tj. moze biti rijec samo o jednoj nultocki, uracunatoj vise puta). Sad je jasno (?) zasto se ti brojevi podudaraju.
[quote](ii) [latex]\alpha[/latex] je nultočka kratnosti [latex]l[/latex] neke derivacije [latex]f^{(i)} (i>0)[/latex], ali nije nultočka od [latex]f^{(i-1)}[/latex]. Tada je [latex]f^{(i)}(\alpha)=\cdots=f^{(i+l-1)}(\alpha)=0, f^{(i+l)}\neq 0[/latex]. Kao i u (i), dobivamo [latex]l[/latex] promjena predznaka u podnizu [latex]f^{(i)},\ldots,f^{(i+l)}[/latex]. Nadalje:
[latex]\displaystyle f^{(i-1)}(\alpha+h)=f^{(i-1)}(\alpha)+\frac{f^{(i+l)}(\alpha)}{(l+1)!}h^{l+1}+\ldots\\ f^{(i)}(\alpha+h)=\frac{f^{(i+l)}(\alpha)}{l!}h^l+\ldots[/latex]
Ako je [latex]l[/latex] paran, nikoji od [latex]f^{(i-1)},f^{(i)}[/latex] ne mijenja predznak, pa je broj promjena [latex]l[/latex] [i][color=red](Zašto ne mijenjaju predznak i zašto ih je baš [latex]l[/latex]?)[/color][/i].[/quote]
[latex]f^{(i)}[/latex] ne mijenja predznak jer [latex]h[/latex] dolazi na parnu potenciju. Zasto [latex]f^{(i-1)}[/latex] ne mijenja predznak... hm, rekao bih da uvijek mozemo naci [latex]h_0[/latex] t. d. je [latex]\forall\,h\le h_0[/latex] [latex]\frac{f^{(i+l)}(\alpha)}{(l+1)!}h^{l+1}+\cdots[/latex]
(tj. nekonstantni dio reda) po modulu strogo manji od [latex]f^{(i-1)}(\alpha)[/latex].
[quote]Ako je [latex]l[/latex] neparan, [latex]f^{(i)}[/latex] mijenja predznak ako [latex]f^{(i-1)}[/latex] ne mijenja [i][color=red](Zašto?)[/color][/i],[/quote]
Ovaj dio mi je mutan... iz prethodnih je napomena jasno zasto [latex]f^{(i-1)}[/latex] ne mijenja predznak i zasto bi [latex]f^{(i)}[/latex] trebao mijenjati, samo me svrha "ako" price zbunjuje. Uglavnom, (recimo da) tvrdnje stoje.
[quote]pa postoji i druga promjena predznaka [i][color=red](Koja druga promjena?)[/color][/i] ,[/quote]
Promjena izmedju [latex]f^{(i-1)}[/latex] i [latex]f^{(i)}[/latex]. Naime, za sve vece [latex]i[/latex] vec smo ustanovili da je broj tih promjena [latex]l[/latex].
[quote]te ih ukupno ima [latex]l\pm1[/latex] [i][color=red](Zašto baš toliko?)[/color][/i], što je opet paran broj.[/quote]
Zato sto gledamo samo lijevog susjeda od [latex]f^{(i)}[/latex], kojem se promijenio predznak.
[quote]Iz (i) i (ii) slijedi tvrdnja (primijetimo da za isti [latex]\alpha[/latex] ne mogu nastupiti oba slučaja).[i][color=red](Zašto točno ne mogu nastupiti oba slučaja? I kako znamo da (i) i (ii) pokrivaju sve mogućnosti?)[/color][/i].[/quote]
Rekao bih da je rezon ovakav: [latex]\alpha[/latex] jest nutocka -- slucaj (i), ili nije, ali vrijedi (ii). To zbilja iscrpljuje sve slucajeve, jer je [latex]\delta[/latex] konstantna za sve [latex]\alpha[/latex] koji ne zadovoljavaju niti (i) niti (ii). Naime, mi citavo vrijeme akumuliramo [i]razlike[/i] promjena broja predznaka po intervalu [latex]\[a,b\][/latex].
Nadam se da sve ovo ima nekog smisla :/
| Citat: | Dokaz:Najprije primijetimo da se 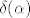 mijenja samo ako mijenja samo ako  prolazi kroz nultočku neke od derivacija prolazi kroz nultočku neke od derivacija 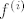 . (Evo ja već ne razumijem zašto mora prolaziti? I što znači da . (Evo ja već ne razumijem zašto mora prolaziti? I što znači da  prolazi kroz nultočku?). prolazi kroz nultočku?). |
Hoce se reci: uzmimo da je  na pocetku jednak jednom kraju intervala na pocetku jednak jednom kraju intervala 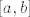 , te ga pustimo da putuje prema drugom kraju – shvati to kao "autoinkrement" (odnosno, "autodekrement") od , te ga pustimo da putuje prema drugom kraju – shvati to kao "autoinkrement" (odnosno, "autodekrement") od  , kad bi takvo sto u , kad bi takvo sto u  bilo moguce definirati. Dakle, ako u tom intervalu postoji nultocka polinoma bilo moguce definirati. Dakle, ako u tom intervalu postoji nultocka polinoma  , ,  mora kroz nju proci. mora kroz nju proci.
| Citat: | Da bismo izračunali broj promjena predznaka, razlikujemo dva slučaja:
(i)  je nultočka od f kratnosti m. U tom slučaju je nultočka od f kratnosti m. U tom slučaju 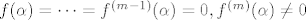 . Prema Taylorovoj formuli: . Prema Taylorovoj formuli:
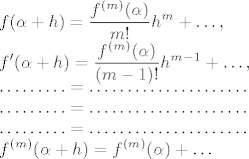 . .
Za dovoljno malo h izrazi napisani na desnim stranama ovih jednakosti dominantni su (Što to znači da su dominantni?) |
Vjerojatno se misli na to da prvi ne-nul clan Taylorovog reda, uz uvjet da je 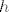 "dovoljno mali", po modulu dominira nad ostatkom reda. "dovoljno mali", po modulu dominira nad ostatkom reda.
| Citat: | i ako h prolazi s pozitivnih na negativne vrijednosti, broj promjena predznaka u podnizu  niza (*) jest m (Što znači da h prolazi s pozitivnih na negativne vrijednosti? I zašto je baš m promjena predznaka?), niza (*) jest m (Što znači da h prolazi s pozitivnih na negativne vrijednosti? I zašto je baš m promjena predznaka?), |
Primijeti koliko je vazan smjer u kojem 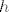 mijenja vrijednosti, odnosno gleda se okolina od mijenja vrijednosti, odnosno gleda se okolina od  s desna na lijevo. Parne potencije od s desna na lijevo. Parne potencije od 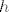 , bio , bio 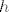 pozitivan ili negativan, daju pozitivne vrijednosti, dok neparne potencije za negativni pozitivan ili negativan, daju pozitivne vrijednosti, dok neparne potencije za negativni 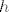 daju negativne vrijednosti. Sad malo upogoni mastu (a.k.a. olovku) i vidjet ces da je broj promjena predznaka kroz daju negativne vrijednosti. Sad malo upogoni mastu (a.k.a. olovku) i vidjet ces da je broj promjena predznaka kroz  upravo upravo  . (Svaka negativna vrijednost generira po jednu promjenu predznaka sa svakim susjedom.) . (Svaka negativna vrijednost generira po jednu promjenu predznaka sa svakim susjedom.)
| Citat: | | a taj se broj podudara i s brojem prijeđenih nultočaka.(Koje su to prijeđene nultočke i zašto se ti brojevi podudaraju?). |
Mozda je problem u nepreciznoj formulaciji teorema: kad se spominje broj nultocki, misli se na njihovu kratnost (tj. moze biti rijec samo o jednoj nultocki, uracunatoj vise puta). Sad je jasno (?) zasto se ti brojevi podudaraju.
| Citat: | (ii)  je nultočka kratnosti je nultočka kratnosti 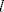 neke derivacije neke derivacije 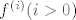 , ali nije nultočka od , ali nije nultočka od 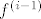 . Tada je . Tada je 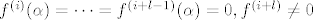 . Kao i u (i), dobivamo . Kao i u (i), dobivamo 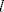 promjena predznaka u podnizu promjena predznaka u podnizu 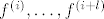 . Nadalje: . Nadalje:
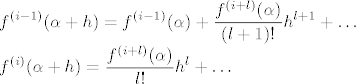
Ako je 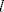 paran, nikoji od paran, nikoji od 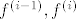 ne mijenja predznak, pa je broj promjena ne mijenja predznak, pa je broj promjena 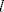 (Zašto ne mijenjaju predznak i zašto ih je baš (Zašto ne mijenjaju predznak i zašto ih je baš 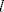 ?). ?). |
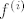 ne mijenja predznak jer ne mijenja predznak jer 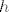 dolazi na parnu potenciju. Zasto dolazi na parnu potenciju. Zasto 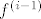 ne mijenja predznak... hm, rekao bih da uvijek mozemo naci ne mijenja predznak... hm, rekao bih da uvijek mozemo naci 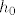 t. d. je t. d. je  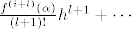
(tj. nekonstantni dio reda) po modulu strogo manji od 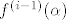 . .
| Citat: | Ako je 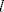 neparan, neparan, 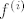 mijenja predznak ako mijenja predznak ako 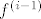 ne mijenja (Zašto?), ne mijenja (Zašto?), |
Ovaj dio mi je mutan... iz prethodnih je napomena jasno zasto 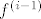 ne mijenja predznak i zasto bi ne mijenja predznak i zasto bi 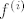 trebao mijenjati, samo me svrha "ako" price zbunjuje. Uglavnom, (recimo da) tvrdnje stoje. trebao mijenjati, samo me svrha "ako" price zbunjuje. Uglavnom, (recimo da) tvrdnje stoje.
| Citat: | | pa postoji i druga promjena predznaka (Koja druga promjena?) , |
Promjena izmedju 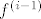 i i 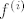 . Naime, za sve vece . Naime, za sve vece  vec smo ustanovili da je broj tih promjena vec smo ustanovili da je broj tih promjena 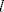 . .
| Citat: | te ih ukupno ima  (Zašto baš toliko?), što je opet paran broj. (Zašto baš toliko?), što je opet paran broj. |
Zato sto gledamo samo lijevog susjeda od 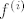 , kojem se promijenio predznak. , kojem se promijenio predznak.
| Citat: | Iz (i) i (ii) slijedi tvrdnja (primijetimo da za isti  ne mogu nastupiti oba slučaja).(Zašto točno ne mogu nastupiti oba slučaja? I kako znamo da (i) i (ii) pokrivaju sve mogućnosti?). ne mogu nastupiti oba slučaja).(Zašto točno ne mogu nastupiti oba slučaja? I kako znamo da (i) i (ii) pokrivaju sve mogućnosti?). |
Rekao bih da je rezon ovakav:  jest nutocka – slucaj (i), ili nije, ali vrijedi (ii). To zbilja iscrpljuje sve slucajeve, jer je jest nutocka – slucaj (i), ili nije, ali vrijedi (ii). To zbilja iscrpljuje sve slucajeve, jer je  konstantna za sve konstantna za sve  koji ne zadovoljavaju niti (i) niti (ii). Naime, mi citavo vrijeme akumuliramo razlike promjena broja predznaka po intervalu koji ne zadovoljavaju niti (i) niti (ii). Naime, mi citavo vrijeme akumuliramo razlike promjena broja predznaka po intervalu 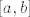 . .
Nadam se da sve ovo ima nekog smisla 
|




