| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
C
Forumaš(ica)

Pridružen/a: 29. 01. 2005. (17:27:47)
Postovi: (4C)16
Spol: 
|
 Postano: 16:13 pet, 14. 4. 2006 Naslov: Postano: 16:13 pet, 14. 4. 2006 Naslov: |
    |
|
|
Hvala na detaljnom objasnjenju, sad mi je jasno : :) - zao mi je ako sam pilio, neki puta me jako muci kad ne skuzim neku "sitnicu" :oops:
Ono gore sam krivo napisao, trebalo je stajati ((x,sin1/x);x e <0,e>), ali jednostavnije (sto mene u stvari muci):
Neka su A i B (<=R) otvoreni, neprazni i disjunktni tako da je AuB=<0,1>. Kako znamo da postoji e>0 takav da je <0,e> <= A ili <0,e> <=B
(intuitivno bih dao ruku u vatru da postoji, ali ne znam dokazati;
kada nebi postojao, znacilo bi da za svaki e>0 <0,e> sijece i A i B, ali sto dalje?)
Hvala na detaljnom objasnjenju, sad mi je jasno :  - zao mi je ako sam pilio, neki puta me jako muci kad ne skuzim neku "sitnicu" - zao mi je ako sam pilio, neki puta me jako muci kad ne skuzim neku "sitnicu" 
Ono gore sam krivo napisao, trebalo je stajati ((x,sin1/x);x e <0,e>), ali jednostavnije (sto mene u stvari muci):
Neka su A i B (<=R) otvoreni, neprazni i disjunktni tako da je AuB=<0,1>. Kako znamo da postoji e>0 takav da je <0,e> <= A ili <0,e> <=B
(intuitivno bih dao ruku u vatru da postoji, ali ne znam dokazati;
kada nebi postojao, znacilo bi da za svaki e>0 <0,e> sijece i A i B, ali sto dalje?)
|
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)

Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
 Postano: 21:40 sub, 15. 4. 2006 Naslov: Postano: 21:40 sub, 15. 4. 2006 Naslov: |
    |
|
|
Ako su A i B (<=R) otvoreni, neprazni i disjunktni tako da je AuB=<0,1> onda je <0,1> nepovezan. S druge strane lako se pokazuje da nema neprekidne surjekcije sa <0,1> na {0,1} (pretpostavi se da ima pa se prije ili kasnije naleti na prekid) pa je <0,1> povezan. Dakle, ako su A i B (<=R) otvoreni, neprazni i disjunktni tako da je AuB=<0,1> onda je <0,1> povezan i nepovezan pa možeš dokazati što god želiš. :D :D :D
Ako su A i B (<=R) otvoreni, neprazni i disjunktni tako da je AuB=<0,1> onda je <0,1> nepovezan. S druge strane lako se pokazuje da nema neprekidne surjekcije sa <0,1> na {0,1} (pretpostavi se da ima pa se prije ili kasnije naleti na prekid) pa je <0,1> povezan. Dakle, ako su A i B (<=R) otvoreni, neprazni i disjunktni tako da je AuB=<0,1> onda je <0,1> povezan i nepovezan pa možeš dokazati što god želiš.   
|
|
| [Vrh] |
|
C
Forumaš(ica)

Pridružen/a: 29. 01. 2005. (17:27:47)
Postovi: (4C)16
Spol: 
|
 Postano: 11:09 ned, 16. 4. 2006 Naslov: Postano: 11:09 ned, 16. 4. 2006 Naslov: |
    |
|
|
Ovo ce zvucati kao da sam malo spor (ako nije ocito do sada :) ) - to znaci da je nemoguce da takvi postoje s obzirom da su povezani skupovi
oni koji nisu nepovezani - kriva pretpostavka.
Ali, u slucaju <0,1> <= AuB, (ostalo isto kao gore) bi tvrdnja bi vjerojatno vrijedila?
Moram priznati da me malo zbunjuje da su za rjesavanje primjera 1.4 potrebne tvrdnje i pojmovi koji dolaze poslije njega (u skripti).
No, anyway Unnamed One++, lijepo se najedi i sve drugo sto cini tvoj Uskrs sretnim. :D
Ovo ce zvucati kao da sam malo spor (ako nije ocito do sada  ) - to znaci da je nemoguce da takvi postoje s obzirom da su povezani skupovi ) - to znaci da je nemoguce da takvi postoje s obzirom da su povezani skupovi
oni koji nisu nepovezani - kriva pretpostavka.
Ali, u slucaju <0,1> <= AuB, (ostalo isto kao gore) bi tvrdnja bi vjerojatno vrijedila?
Moram priznati da me malo zbunjuje da su za rjesavanje primjera 1.4 potrebne tvrdnje i pojmovi koji dolaze poslije njega (u skripti).
No, anyway Unnamed One++, lijepo se najedi i sve drugo sto cini tvoj Uskrs sretnim. 
|
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)

Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
 Postano: 18:43 ned, 16. 4. 2006 Naslov: Postano: 18:43 ned, 16. 4. 2006 Naslov: |
    |
|
|
Zašto "spor", pa ipak je analiza 3 jedan od najtežih kolegija na drugoj godini (ako ne i šire...). :wink:
Za <0,1> <= AuB kad su A, B otvoreni (u R), neprazni, disjunktni je čak i <0,1>=A ili <0,1>=B jer bi inače skupovi
C:=A {presjek} <0,1>
D:=B {presjek} <0,1>
bili neprazni, disjunktni i ovoreni (u R, ali i u <0,1>) pa bi zbog
CuD=<0,1>
<0,1> bio nepovezan.
Skripta iz analize 3 je po mom mišljenju pisana prilično pedantno t.d. sam siguran da za rjesavanje primjera 1.4 nisu bile potrebne tvrdnje i pojmovi koji dolaze poslije njega (samo što ga ja drugačije nisam znao riješiti :( ).
Zašto "spor", pa ipak je analiza 3 jedan od najtežih kolegija na drugoj godini (ako ne i šire...). 
Za <0,1> <= AuB kad su A, B otvoreni (u R), neprazni, disjunktni je čak i <0,1>=A ili <0,1>=B jer bi inače skupovi
C:=A {presjek} <0,1>
D:=B {presjek} <0,1>
bili neprazni, disjunktni i ovoreni (u R, ali i u <0,1>) pa bi zbog
CuD=<0,1>
<0,1> bio nepovezan.
Skripta iz analize 3 je po mom mišljenju pisana prilično pedantno t.d. sam siguran da za rjesavanje primjera 1.4 nisu bile potrebne tvrdnje i pojmovi koji dolaze poslije njega (samo što ga ja drugačije nisam znao riješiti  ). ).
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 9:15 pon, 19. 6. 2006 Naslov: Postano: 9:15 pon, 19. 6. 2006 Naslov: |
    |
|
|
Ovako se pokazivalo na MA1,pa reci ako na to ne mislis...
Naime povrsinu trokuta "znamo" : P=1/2*a*b*sin(alfa) ; alfa je kut izmedu stranice a,b. No,podijelis krug na n trokuta tako da je kuta alfa ima vrh u sredistu kruga. No, tada je povrsina kruga : lim(n->besk) n* P= lim (n->besk) n* 1/2*a*b*sin(alfa)={ no sada uocis da je a=b=r , r -radijus kruga , dok je alfa=2pi/n , } = lim (n->besk) n*(1/2*r*r*sin(2pi/n))={ pomnozis,podijelis sa 2pi }= lim (n->besk) r^2*pi* (sin(2pi/n)/(2pi/n))={ no,kada n->besk tada 2pi/n->o, a lim(x->o) sinx/x=1 ,dobivas } = r^2 *pi lim(n->besk) (sin(2pi/n)/(2pi/n)) ={ iskoristis limes } =r^2 *pi*1= r^2*pi.
Ako se ne varam na usmenom je prof. Ungar to znao pitati ,ali mislim da je to bilo u kontekstu integrala ,ali ovo je prilicno dobro objasnjenje. Reci ako na to nisi mislio/la.
Ovako se pokazivalo na MA1,pa reci ako na to ne mislis...
Naime povrsinu trokuta "znamo" : P=1/2*a*b*sin(alfa) ; alfa je kut izmedu stranice a,b. No,podijelis krug na n trokuta tako da je kuta alfa ima vrh u sredistu kruga. No, tada je povrsina kruga : lim(n->besk) n* P= lim (n->besk) n* 1/2*a*b*sin(alfa)={ no sada uocis da je a=b=r , r -radijus kruga , dok je alfa=2pi/n , } = lim (n->besk) n*(1/2*r*r*sin(2pi/n))={ pomnozis,podijelis sa 2pi }= lim (n->besk) r^2*pi* (sin(2pi/n)/(2pi/n))={ no,kada n->besk tada 2pi/n->o, a lim(x->o) sinx/x=1 ,dobivas } = r^2 *pi lim(n->besk) (sin(2pi/n)/(2pi/n)) ={ iskoristis limes } =r^2 *pi*1= r^2*pi.
Ako se ne varam na usmenom je prof. Ungar to znao pitati ,ali mislim da je to bilo u kontekstu integrala ,ali ovo je prilicno dobro objasnjenje. Reci ako na to nisi mislio/la.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 11:15 pon, 19. 6. 2006 Naslov: Postano: 11:15 pon, 19. 6. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]da, profesor to pita oko integrala, pokusavo sam standardnom parametrizacijom x=rcos(fi) y=rsin(fi) ali na kraju mi integriranjem ne ispadne bas kak bi trebalo, ovo tvoje je ok valjda ce profesoru to bit dovoljno ak me pita.[/quote]
Pogledaj si u biljeznicu (iz vjezbi) ili u skriptu,tamo ti to zasigurno pise.
Siguran sam da ce traziti da izracunas preko integrala,pa ti savjetujem da malo bolje pogledas,ipak ovaj nacin je "pre-elementaran" za MA3. Puno srece na usmenom :D .
| Anonymous (napisa): | | da, profesor to pita oko integrala, pokusavo sam standardnom parametrizacijom x=rcos(fi) y=rsin(fi) ali na kraju mi integriranjem ne ispadne bas kak bi trebalo, ovo tvoje je ok valjda ce profesoru to bit dovoljno ak me pita. |
Pogledaj si u biljeznicu (iz vjezbi) ili u skriptu,tamo ti to zasigurno pise.
Siguran sam da ce traziti da izracunas preko integrala,pa ti savjetujem da malo bolje pogledas,ipak ovaj nacin je "pre-elementaran" za MA3. Puno srece na usmenom  . .
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
akki
Forumaš(ica)


Pridružen/a: 28. 09. 2004. (14:55:35)
Postovi: (88)16
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 13:52 sub, 24. 6. 2006 Naslov: Postano: 13:52 sub, 24. 6. 2006 Naslov: |
    |
|
|
Neka su V i W vektorski prostori nad poljem F. Kazemo da je [latex]A:V\rightarrow W[/latex] [b]linearni operator[/b] ako vrijedi:
(1) [latex]\forall x,y\in V, \forall \alpha,\beta \in F \Rightarrow A(\alpha*x+\beta*y)=\alpha*A(x)+\beta*A(y)[/latex]
(2) [latex]\forall x \in V, \forall \lambda \in F \Rightarrow A(\lambda*x)=\lambda*A(x)[/latex]
(primjeti da sam stavio alfu i betu kao elemente F jer F moze biti bilo koje polje skalara, ne nuzno skup realnih brojeva.)
za monotonost niza se tocne definicije ne mogu sjetit pa cu napisat definiciju monotone fcije:
Neka je [latex]f:I\rightarrow R[/latex] funkcija, [latex]I\subseteq R[/latex] otvoren interval. Kazemo da je fukcija f monotona ako:
[latex]\forall x_1, x_2 \in I, x_1 \leq x_2 \Rightarrow f(x_1)\leq f(x_2)[/latex]
Funkcija je strogo monotona ako vrijede stroge nejednakosti.
gornja definicija je za rastucu (odnosno strogo rastucu) funkciju. ukoliko se radi o padajucoj fukciji, dovoljno je okrenuti nejednakosti. u tom slucaju:
[latex]\forall x_1, x_2 \in I, x_1 \geq x_2 \Rightarrow f(x_1)\geq f(x_2)[/latex]
HTH.
EDIT: za matrice pogledaj ovamo:
http://en.wikipedia.org/wiki/Matrix
;-)
DISCLAMER: definicije su pisane po sjecanju. ako sam igdje pogrijesio, molim da me se ispravi. zahvaljujem :-)
Neka su V i W vektorski prostori nad poljem F. Kazemo da je 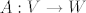 linearni operator ako vrijedi: linearni operator ako vrijedi:
(1) 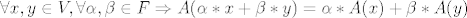
(2) 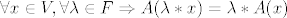
(primjeti da sam stavio alfu i betu kao elemente F jer F moze biti bilo koje polje skalara, ne nuzno skup realnih brojeva.)
za monotonost niza se tocne definicije ne mogu sjetit pa cu napisat definiciju monotone fcije:
Neka je 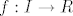 funkcija, funkcija, 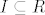 otvoren interval. Kazemo da je fukcija f monotona ako: otvoren interval. Kazemo da je fukcija f monotona ako:
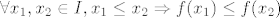
Funkcija je strogo monotona ako vrijede stroge nejednakosti.
gornja definicija je za rastucu (odnosno strogo rastucu) funkciju. ukoliko se radi o padajucoj fukciji, dovoljno je okrenuti nejednakosti. u tom slucaju:
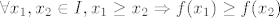
HTH.
EDIT: za matrice pogledaj ovamo:
http://en.wikipedia.org/wiki/Matrix

DISCLAMER: definicije su pisane po sjecanju. ako sam igdje pogrijesio, molim da me se ispravi. zahvaljujem 
Zadnja promjena: HijenA; 15:52 sub, 24. 6. 2006; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
 Postano: 14:07 sub, 24. 6. 2006 Naslov: Postano: 14:07 sub, 24. 6. 2006 Naslov: |
    |
|
|
Da dopunim kolegu Hijenu -- niz je funkcija iz N u X (gdje je X neki skup, R, Q, N, stagod), pa je monoton niz monotona funkcija iz N u X... :)
'ave fun!
Sinisa
Da dopunim kolegu Hijenu -- niz je funkcija iz N u X (gdje je X neki skup, R, Q, N, stagod), pa je monoton niz monotona funkcija iz N u X... 
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
Zadnja promjena: cinik; 15:36 sub, 24. 6. 2006; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
|
| [Vrh] |
|
akki
Forumaš(ica)


Pridružen/a: 28. 09. 2004. (14:55:35)
Postovi: (88)16
|
|
| [Vrh] |
|
|











