| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ivan33
Gost
|
|
| [Vrh] |
|
lhranjec
Forumaš(ica)

Pridružen/a: 06. 12. 2002. (11:04:45)
Postovi: (42)16
|
|
| [Vrh] |
|
johnny
Forumaš(ica)

Pridružen/a: 09. 02. 2005. (14:12:26)
Postovi: (23)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 1:11 ned, 18. 6. 2006 Naslov: Postano: 1:11 ned, 18. 6. 2006 Naslov: |
    |
|
|
[quote="johnny"]Molim vas jel bi netko mogao objasniti metodu kontrakcije? Sad kad vjezbam ove dodatne zadatke shvatio sam da ne kuzim bas tu metodu previse,a na vjezbama smo rijesili svega 1 primjer
Stoga ako bi netko mogao malo pojasniti princip i postupak u slucaju da je f(x)=x^2+4sinx-1 ili za bilo koju drugu funkciju ako je lakse :)[/quote]
f(x)=0
x^2+4sinx-1=0
Možemo promatrati slijedeće:
x^2-1=-4sinx
Ja sam krenuo ovako rješavati:
[latex]sinx=\frac{-1}{4}x^2-\frac{1}{4}[/latex]
Sada nacrtaš graf od sinx i graf desne strane i viditi ćeš da se oni sjeku u 2 točke - te 2 točke će biti nultočke od f(x).
Idući korak je ocijeniti gdje se nalaze te točke.
Pretpostavljam da se točka nalazi između 0 i 0.5.
sin0=0
sin.5=0.479
0.25(0)^2+0.25=0.25
0.25(1/2)^2+0.25=0.1875
Ako nacrtaš sliku sa ovim vrijednostima, biti će jasno da se tamo sijeku sinx i -0.25x^2+0.25
Označimo sada sa q(x) desnu stranu, tj.
[latex]q(x)=\frac{-1}{4}x^2-\frac{1}{4}[/latex]
Provjeravamo uvjete:
1. Očito je klase C na [0,0.5]
Moramo još provjeriti da li vrijedi
[latex]q([0,0.5])\subset[0,0.5][/latex]
[latex]q([0,0.5])=[q(0),q(0.5)]=[\frac{1}{4},\frac{3}{16}]\subset[0,0.5][/latex]
Još moramo provjeriti da li vrijedi slijedeće:
[latex]q=M_1=max_{x \in [0,0.5]}|q'(x)|<1\\
q'(x)=-\frac{1}{2}x
[/latex]
Očito je maksimum od |q'(x)| na rubu intervala, tj. u točki 0.5, pa je q=1/4
Trebati će nam slijedeće
[latex]\frac{q}{1-q}=\frac{1}{3}[/latex] jer vrijedi:
[latex]|x_n-x_{n-1}|<\frac{q}{1-q}\epsilon=0.00033[/latex]
Sad imamo sve što nam treba. Uzmimo sad za [latex]x_0[/latex] polovište intervala [0,0.5], tj. 0.25
[latex]x_1=q(x_0)=0.234375[/latex]
[latex]x_2=q(x_0)=0.2360444 \\
x_2-x_1=0.00022<0.00033[/latex]
Jedna nultočka je x2.
Drugu probaj sam(a).
| johnny (napisa): | Molim vas jel bi netko mogao objasniti metodu kontrakcije? Sad kad vjezbam ove dodatne zadatke shvatio sam da ne kuzim bas tu metodu previse,a na vjezbama smo rijesili svega 1 primjer
Stoga ako bi netko mogao malo pojasniti princip i postupak u slucaju da je f(x)=x^2+4sinx-1 ili za bilo koju drugu funkciju ako je lakse  |
f(x)=0
x^2+4sinx-1=0
Možemo promatrati slijedeće:
x^2-1=-4sinx
Ja sam krenuo ovako rješavati:
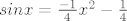
Sada nacrtaš graf od sinx i graf desne strane i viditi ćeš da se oni sjeku u 2 točke - te 2 točke će biti nultočke od f(x).
Idući korak je ocijeniti gdje se nalaze te točke.
Pretpostavljam da se točka nalazi između 0 i 0.5.
sin0=0
sin.5=0.479
0.25(0)^2+0.25=0.25
0.25(1/2)^2+0.25=0.1875
Ako nacrtaš sliku sa ovim vrijednostima, biti će jasno da se tamo sijeku sinx i -0.25x^2+0.25
Označimo sada sa q(x) desnu stranu, tj.
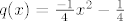
Provjeravamo uvjete:
1. Očito je klase C na [0,0.5]
Moramo još provjeriti da li vrijedi
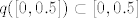
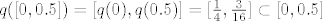
Još moramo provjeriti da li vrijedi slijedeće:
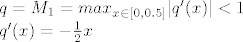
Očito je maksimum od |q'(x)| na rubu intervala, tj. u točki 0.5, pa je q=1/4
Trebati će nam slijedeće
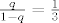 jer vrijedi: jer vrijedi:
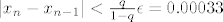
Sad imamo sve što nam treba. Uzmimo sad za  polovište intervala [0,0.5], tj. 0.25 polovište intervala [0,0.5], tj. 0.25
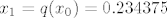
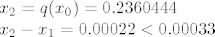
Jedna nultočka je x2.
Drugu probaj sam(a).
_________________
The Dude Abides
|
|
| [Vrh] |
|
Sedma
Forumaš(ica)


Pridružen/a: 29. 04. 2004. (19:28:25)
Postovi: (3B)16
Spol: 
|
 Postano: 11:36 ned, 18. 6. 2006 Naslov: Postano: 11:36 ned, 18. 6. 2006 Naslov: |
    |
|
|
mene samo zanima da li se znaci sinx moze zamjeniti sa g(x) jer koliko sam shvatila na vjezbama, g(x) mozemo izraziti samo ako je x samostalan, ili ga kao takvog moramo izluciti, dakle, ovdje bi to bilo neko korjenovanje ili arcsin...
neznam da li sam ovo bas najspretnije napisala, ali ako me netko shavti molim ga da mi odgovori, jer samo srece da sam ja ipak u krivu :)
mene samo zanima da li se znaci sinx moze zamjeniti sa g(x) jer koliko sam shvatila na vjezbama, g(x) mozemo izraziti samo ako je x samostalan, ili ga kao takvog moramo izluciti, dakle, ovdje bi to bilo neko korjenovanje ili arcsin...
neznam da li sam ovo bas najspretnije napisala, ali ako me netko shavti molim ga da mi odgovori, jer samo srece da sam ja ipak u krivu 
_________________
U tramvaju je petero ljudi, ako izadje sedmero, a na sljedecoj stanici udje dvoje, tramvaj ce biti prazan...
|
|
| [Vrh] |
|
akki
Forumaš(ica)


Pridružen/a: 28. 09. 2004. (14:55:35)
Postovi: (88)16
|
|
| [Vrh] |
|
Sedma
Forumaš(ica)


Pridružen/a: 29. 04. 2004. (19:28:25)
Postovi: (3B)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
lhranjec
Forumaš(ica)

Pridružen/a: 06. 12. 2002. (11:04:45)
Postovi: (42)16
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
Gordan
Forumaš(ica)


Pridružen/a: 03. 11. 2002. (18:01:44)
Postovi: (192)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 22:58 ned, 18. 6. 2006 Naslov: Postano: 22:58 ned, 18. 6. 2006 Naslov: |
    |
|
|
[quote="goranm"]Ne znam, imam par zadataka sa vježbi tako rješenih i daju "ispravan" rezultat. :)[/quote]
To bi mogla biti slučajnost. Naime, ako je bio [latex]q\leq\frac{1}{2}[/latex], onda je [latex]\frac{q}{1-q}\leq\frac{1-q}{q}[/latex] pa smo svejedno dobili točno rješenje (čak smo možda napravili i koji korak više). No ako je [latex]q\geq\frac{1}{2}[/latex], postoji mogućnost da smo prerano završili.
U svakom slučaju, ja ću se držati svojeg kriterija za zaustavljanje. Mislim da imam dobre argumente za slučaj da mi ne priznaju. :)
| goranm (napisa): | Ne znam, imam par zadataka sa vježbi tako rješenih i daju "ispravan" rezultat.  |
To bi mogla biti slučajnost. Naime, ako je bio 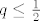 , onda je , onda je 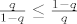 pa smo svejedno dobili točno rješenje (čak smo možda napravili i koji korak više). No ako je pa smo svejedno dobili točno rješenje (čak smo možda napravili i koji korak više). No ako je 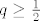 , postoji mogućnost da smo prerano završili. , postoji mogućnost da smo prerano završili.
U svakom slučaju, ja ću se držati svojeg kriterija za zaustavljanje. Mislim da imam dobre argumente za slučaj da mi ne priznaju. 
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
Zadnja promjena: Melkor; 23:43 ned, 18. 6. 2006; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:17 ned, 18. 6. 2006 Naslov: Postano: 23:17 ned, 18. 6. 2006 Naslov: |
    |
|
|
[quote="Melkor"][quote="goranm"]Ne znam, imam par zadataka sa vježbi tako rješenih i daju "ispravan" rezultat. :)[/quote]
To bi mogla biti slučajnost. Naime, ako je bio [latex]q\leq\frac{1}{2}[/latex], onda je [latex]\frac{q}{1-q}\leq\frac{1-q}{q}[/latex]. No ako je [latex]q\geq\frac{1}{2}[/latex], postoji mogućnost da smo prerano završili.
U svakom slučaju, ja ću se držati svojeg kriterija za zaustavljanje. Mislim da imam dobre argumente za slučaj da mi ne priznaju. :)[/quote]
Radili smo i zadatak gdje je q=e^-1, tj. 0.367. Onda ispada da je q/(1-q)=0.58 i kada se to pomnoži sa epsilon=0.005, dobije se 0.0029
Po tome nultočka je x=-1.98907
Da smo radili (1-q)/q, onda bi imali da je (1-q)/q * epsilon = 0.0086, a nultočka je x=-1.200336
E sad, moj grafički kalkulator je za funkciju iz tog zadatka e^x-x-1.5 dao da je nultočka jednaka -1.198290437 što je dosta bliže kada uzimamo q/(1-q) nego (1-q)/q
Edit: sad sam tek pažljivije pročitao što si napisao. Idem probat nać neki primjer di je q>0.5 pa vidit.
@Ilja: nije jasnije :)
| Melkor (napisa): | | goranm (napisa): | Ne znam, imam par zadataka sa vježbi tako rješenih i daju "ispravan" rezultat.  |
To bi mogla biti slučajnost. Naime, ako je bio 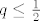 , onda je , onda je 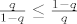 . No ako je . No ako je 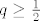 , postoji mogućnost da smo prerano završili. , postoji mogućnost da smo prerano završili.
U svakom slučaju, ja ću se držati svojeg kriterija za zaustavljanje. Mislim da imam dobre argumente za slučaj da mi ne priznaju.  |
Radili smo i zadatak gdje je q=e^-1, tj. 0.367. Onda ispada da je q/(1-q)=0.58 i kada se to pomnoži sa epsilon=0.005, dobije se 0.0029
Po tome nultočka je x=-1.98907
Da smo radili (1-q)/q, onda bi imali da je (1-q)/q * epsilon = 0.0086, a nultočka je x=-1.200336
E sad, moj grafički kalkulator je za funkciju iz tog zadatka e^x-x-1.5 dao da je nultočka jednaka -1.198290437 što je dosta bliže kada uzimamo q/(1-q) nego (1-q)/q
Edit: sad sam tek pažljivije pročitao što si napisao. Idem probat nać neki primjer di je q>0.5 pa vidit.
@Ilja: nije jasnije 
_________________
The Dude Abides
|
|
| [Vrh] |
|
|















