| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 1:21 uto, 20. 6. 2006 Naslov: Postano: 1:21 uto, 20. 6. 2006 Naslov: |
    |
|
|
Pa kad tako lijepo pitaš.......
Pretpostavka je da postoji limes [latex]\lim_{x\to c-}f(x)=L[/latex].
Dakle za [latex]\varepsilon>0[/latex] postoji [latex]\delta>0[/latex] takav da [latex]c-\delta<x<c \ \Rightarrow \ |f'(x)-L|<\varepsilon[/latex].
Za svaki [i]x[/i] takav da je [latex]c-\delta<x<c[/latex] postoji [latex]\xi_x\in\langle x,c\rangle[/latex] tako da vrijedi
[latex]f(x)-f(c)=f'(\xi_x)(x-c)[/latex], tj. [latex]\frac{f(x)-f(c)}{x-c}=f'(\xi_x)[/latex].
Kako je [latex]c-\delta<\xi_x<c[/latex], slijedi [latex]|f'(\xi_x)-L|<\varepsilon[/latex], tj. [latex]|\frac{f(x)-f(c)}{x-c}-L|<\varepsilon[/latex].
Odavde po definiciji zaključujemo da postoji [latex]\lim_{x\to c-}\frac{f(x)-f(c)}{x-c}=L[/latex].
Slično se dobiva za desni limes pa je [latex]f'(c)=L[/latex].
Kako se ovaj teorem primijenjuje na danom primjeru? Pa naprosto prekid prve vrste od f' u točki c je takav prekid da postoje, ali su različiti limesi
[latex]\lim_{x\to c-}f'(x)= \lim_{x\to c+}f'(x)[/latex],
dok iz gornjeg teorema vidimo da oba moraju biti jednaka f'(c).
Konačno, ako uzmeš g zadanu formulom:
g(x)=0 za x<0,
g(x)=1 za x>=0,
onda g ima u 0 prekid prve vrste pa ne može postojati f takva da je f'=g.
Kao posljedica, operator deriviranja nije surjektivan, jel tako Ilja? 8)
----------
Ovo da derivacija nema prekida prve vrste slijedi i iz (malo općenitijeg) [i]Darbouxovog teorema[/i], vidi ovdje:
http://web.math.hr/nastava/analiza/files/tezi_zadaci.pdf
Pa kad tako lijepo pitaš.......
Pretpostavka je da postoji limes 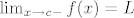 . .
Dakle za 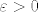 postoji postoji 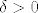 takav da takav da  . .
Za svaki x takav da je 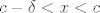 postoji postoji 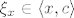 tako da vrijedi tako da vrijedi
 , tj. , tj. 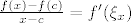 . .
Kako je 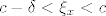 , slijedi , slijedi  , tj. , tj. 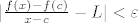 . .
Odavde po definiciji zaključujemo da postoji 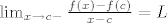 . .
Slično se dobiva za desni limes pa je 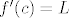 . .
Kako se ovaj teorem primijenjuje na danom primjeru? Pa naprosto prekid prve vrste od f' u točki c je takav prekid da postoje, ali su različiti limesi
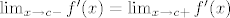 , ,
dok iz gornjeg teorema vidimo da oba moraju biti jednaka f'(c).
Konačno, ako uzmeš g zadanu formulom:
g(x)=0 za x<0,
g(x)=1 za x>=0,
onda g ima u 0 prekid prve vrste pa ne može postojati f takva da je f'=g.
Kao posljedica, operator deriviranja nije surjektivan, jel tako Ilja? 
----------
Ovo da derivacija nema prekida prve vrste slijedi i iz (malo općenitijeg) Darbouxovog teorema, vidi ovdje:
http://web.math.hr/nastava/analiza/files/tezi_zadaci.pdf
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Dick Long
Forumaš(ica)


Pridružen/a: 10. 05. 2006. (13:50:57)
Postovi: (22)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|







