|
Sferne koordinate su dane sa
[latex](x,y,z)=\Phi(r,\varphi,\psi)=(r\cos\psi \cos\varphi, \ r\cos\psi \sin\varphi, \ r\sin\psi)[/latex],
a pripadna Jacobijeva matrica je
[latex]\displaystyle\frac{\partial(x,y,z)}{\partial(r,\varphi,\psi)}=
\left[\begin{array}{ccc}
\cos\psi\cos\varphi & -r\cos\psi\sin\varphi & -r\sin\psi\cos\varphi\\
\cos\psi\sin\varphi & r\cos\psi\cos\varphi & -r\sin\psi\sin\varphi\\
\sin\psi & 0 & r\cos\psi
\end{array}\right][/latex]
Prelazak iz Kartezijevih u sferne koordinate i obratno vrši funkcija [latex]\Phi[/latex]:
[latex]f(x,y,z)=f(\Phi(r,\varphi,\psi))[/latex].
Dakle, ako je je funkcija f zadana u Kartezijevim koordinatama [latex](x,y,z)[/latex], onda je [latex]f\circ \Phi[/latex] ista ta funkcija zadana u sfernim koordinatama.
Prema teoremu o diferencijalu kompozicije imamo:
[latex]D(f\circ \Phi)(r,\varphi,\psi)=Df(\Phi(r,\varphi,\psi))\cdot D\Phi(r,\varphi,\psi)[/latex]
tj. zbog [latex](x,y,z)=\Phi(r,\varphi,\psi)[/latex] imamo
[latex]D(f\circ \Phi)(r,\varphi,\psi)=Df(x,y,z)\cdot D\Phi(r,\varphi,\psi)[/latex],
što matrično zapisano glasi:
[latex]\displaystyle [\partial_r (f\circ \Phi), \partial_\varphi (f\circ \Phi), \partial_\psi (f\circ \Phi)]=
[\partial_x f, \partial_y f, \partial_z f] \cdot\frac{\partial(x,y,z)}{\partial(r,\varphi,\psi)}[/latex],
tj.
[latex]\displaystyle [\partial_r (f\circ \Phi), \partial_\varphi (f\circ \Phi), \partial_\psi (f\circ \Phi)]=\\
=[\partial_x f, \partial_y f, \partial_z f] \cdot\left[\begin{array}{ccc}
\cos\psi\cos\varphi & -r\cos\psi\sin\varphi & -r\sin\psi\cos\varphi\\
\cos\psi\sin\varphi & r\cos\psi\cos\varphi & -r\sin\psi\sin\varphi\\
\sin\psi & 0 & r\cos\psi
\end{array}\right][/latex].
Nas zanimaju [latex]\partial_x f, \partial_y f, \partial_z f[/latex] izraženi pomoću [latex]\partial_r (f\circ \Phi), \partial_\varphi (f\circ \Phi), \partial_\psi (f\circ \Phi)[/latex], s tim da posljednje brojeve kraće pišemo [latex]\partial_r f, \partial_\varphi f, \partial_\psi f[/latex].
To se dobije npr. rješavanjem gornjeg 3x3 sustava ili bolje invertiranjem matrice [latex]\frac{\partial(x,y,z)}{\partial(r,\varphi,\psi)}[/latex] ovako:
[latex]\displaystyle [\partial_x f, \partial_y f, \partial_z f] = [\partial_r f, \partial_\varphi f, \partial_\psi f]
\cdot
\left(\frac{\partial(x,y,z)}{\partial(r,\varphi,\psi)}\right)^{-1}[/latex]
tj.
[latex]\displaystyle [\partial_x f, \partial_y f, \partial_z f]
=[\partial_r f, \partial_\varphi f, \partial_\psi f] \cdot\\ \cdot\frac{1}{r\cos 2\varphi \cos\psi}\left[\begin{array}{ccc}
r\cos^2 \psi \cos\varphi & -r\cos^2 \psi \sin\varphi & r\cos 2\varphi\cos\psi\sin\psi\\
\sin\varphi & -\cos\varphi & 0\\
-\cos\varphi\cos\psi\sin\psi & \sin\varphi\cos\psi\sin\psi & \cos 2\varphi\cos^2\psi
\end{array}\right][/latex]
Sferne koordinate su dane sa
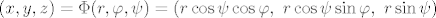 , ,
a pripadna Jacobijeva matrica je
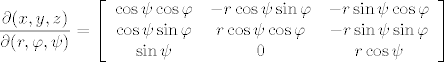
Prelazak iz Kartezijevih u sferne koordinate i obratno vrši funkcija 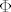 : :
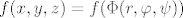 . .
Dakle, ako je je funkcija f zadana u Kartezijevim koordinatama 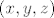 , onda je , onda je 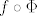 ista ta funkcija zadana u sfernim koordinatama. ista ta funkcija zadana u sfernim koordinatama.
Prema teoremu o diferencijalu kompozicije imamo:
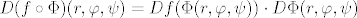
tj. zbog 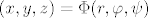 imamo imamo
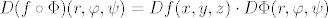 , ,
što matrično zapisano glasi:
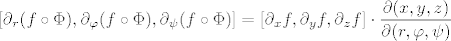 , ,
tj.
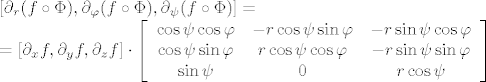 . .
Nas zanimaju 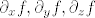 izraženi pomoću izraženi pomoću 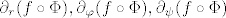 , s tim da posljednje brojeve kraće pišemo , s tim da posljednje brojeve kraće pišemo 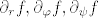 . .
To se dobije npr. rješavanjem gornjeg 3x3 sustava ili bolje invertiranjem matrice 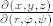 ovako: ovako:
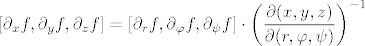
tj.
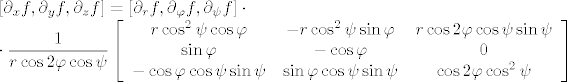
|





