| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
MajaM
Gost
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 22:31 ned, 18. 6. 2006 Naslov: Postano: 22:31 ned, 18. 6. 2006 Naslov: |
    |
|
|
[latex]2x e^y dx + (x^2-y^2-2y) dy = 0[/latex]
Pomnožimo jednadžbu s [latex]e^{\psi(y)}[/latex] za neku funkciju [latex]\psi[/latex].
[latex]2x e^{y+\psi(y)} dx + (x^2-y^2-2y) e^{\psi(y)} dy = 0[/latex]
Da bi ova jednadžba bila egzaktna, mora vrijediti:
[latex]2x e^{y+\psi(y)} (1+\psi'(y))=2x e^{\psi(y)}[/latex],
odakle dobivamo
[latex]\psi(y)=-e^{-y}-y[/latex]
Dakle, imamo egzaktnu jednadžbu
[latex]2x e^{-e^{-y}} dx + (x^2-y^2-2y) e^{-e^{-y}-y} dy = 0[/latex]
čiji prvi integral je
[latex]f(x,y)=(x^2-y^2-2y) e^{-e^{-y}}+ \int 2(y+1)e^{-e^{-y}}dy = C[/latex]
Posljednji integral se, čini se, ne može elementarno izračunati, barem Mathematica to ne zna.
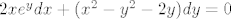
Pomnožimo jednadžbu s 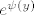 za neku funkciju za neku funkciju 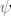 . .
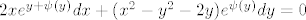
Da bi ova jednadžba bila egzaktna, mora vrijediti:
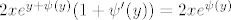 , ,
odakle dobivamo
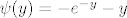
Dakle, imamo egzaktnu jednadžbu
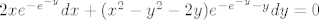
čiji prvi integral je
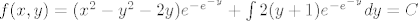
Posljednji integral se, čini se, ne može elementarno izračunati, barem Mathematica to ne zna.
|
|
| [Vrh] |
|
suziQ
Forumaš(ica)


Pridružen/a: 29. 05. 2005. (13:52:50)
Postovi: (2B)16
Spol: 
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
MajaM
Gost
|
|
| [Vrh] |
|
Daya
Forumaš(ica)


Pridružen/a: 20. 02. 2006. (02:00:09)
Postovi: (2F)16
Spol: 
|
 Postano: 2:55 pet, 23. 6. 2006 Naslov: Postano: 2:55 pet, 23. 6. 2006 Naslov: |
    |
|
|
[quote="MajaM"]2. ako mi netko pliz moze ukratko objasniti metodu integracijskog multiplikatora.[/quote]
Ovdje bas i nemas neke potpune sablone.. Pokusat cu najkrace i najjednostavnije..
Dakle, imas jednadzbu [latex]f_1 (x, y) + f_2 (x, y)\cdot y' = 0[/latex] koja nije egzaktna..
Trazis [latex]\mu (x,y)[/latex] t.d. novo dobivena jednadzba
[latex]y'=- \frac {f_1(x, y)\cdot \mu (x, y)} {f_2(x, y)\cdot \mu (x, y)}[/latex]
bude egzaktna.
Najvaznija ti je sljedeca formula:
[latex]\frac {1} {\mu}\cdot \mu '= \frac
{\frac {\partial f_1} {\partial y} - \frac {\partial f_2} {\partial x}}
{\frac {\partial v} {\partial x}\cdot f_2 - \frac {\partial v} {\partial y}\cdot f_1}[/latex]
Sad je problem naci funkciju v(x, y) koja bi zadovoljavala gornju formulu..
Nju prakticki pogadjas (ali s vremenom ti bude gotovo uvijek jasno koju moras uzeti)..
Da bi lakse izabrala funkciju v(x, y) u formuli si prvo uvrsti sve sto mozes (funkcije f_1, f_2, njihove parcijalne derivacije), bit ce ti lakse vidjeti.
Najcesce funkciju v biras izmedju:
[latex]v = x[/latex]
[latex]v = y[/latex]
[latex]v = xy[/latex]
[latex]v = \frac {x} {y}[/latex]
[latex]v = x^2 + y^2[/latex]
Naravno, to nisu jedine, ali mislim da se ove najcesce pojavljuju..
Ako imas neku trigonometrijsku funkciju, onda najcesce za v trebas uzeti to sto se nalazi unutar te trigonometrijske funkcije.
Stvar je u tome da na desnoj strani u onoj formuli moras dobiti neku funkciju u ovisnosti samo o funkciji v (znaci, kad zamjenis sa v ono sto mozes - sto si izabrala, ostali x-evi i y-i bi ti se trebali pokratiti ako si dobro izabrala funkciju v)..
I onda rjesavas dobivenu ODJ i dobijes [latex]\mu = ...[/latex] koji mnozis sa pocetnom jednadzbom kao u formuli gore..
Nadam se da sam pomogla.. :wink:
(i da nema grjesaka u formulama :roll: )
| MajaM (napisa): | | 2. ako mi netko pliz moze ukratko objasniti metodu integracijskog multiplikatora. |
Ovdje bas i nemas neke potpune sablone.. Pokusat cu najkrace i najjednostavnije..
Dakle, imas jednadzbu 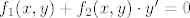 koja nije egzaktna.. koja nije egzaktna..
Trazis 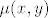 t.d. novo dobivena jednadzba t.d. novo dobivena jednadzba
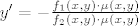
bude egzaktna.
Najvaznija ti je sljedeca formula:
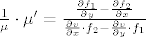
Sad je problem naci funkciju v(x, y) koja bi zadovoljavala gornju formulu..
Nju prakticki pogadjas (ali s vremenom ti bude gotovo uvijek jasno koju moras uzeti)..
Da bi lakse izabrala funkciju v(x, y) u formuli si prvo uvrsti sve sto mozes (funkcije f_1, f_2, njihove parcijalne derivacije), bit ce ti lakse vidjeti.
Najcesce funkciju v biras izmedju:

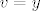
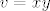

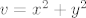
Naravno, to nisu jedine, ali mislim da se ove najcesce pojavljuju..
Ako imas neku trigonometrijsku funkciju, onda najcesce za v trebas uzeti to sto se nalazi unutar te trigonometrijske funkcije.
Stvar je u tome da na desnoj strani u onoj formuli moras dobiti neku funkciju u ovisnosti samo o funkciji v (znaci, kad zamjenis sa v ono sto mozes - sto si izabrala, ostali x-evi i y-i bi ti se trebali pokratiti ako si dobro izabrala funkciju v)..
I onda rjesavas dobivenu ODJ i dobijes 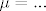 koji mnozis sa pocetnom jednadzbom kao u formuli gore.. koji mnozis sa pocetnom jednadzbom kao u formuli gore..
Nadam se da sam pomogla.. 
(i da nema grjesaka u formulama  ) )
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|








